2019_2020学年高中数学第二章基本初等函数(Ⅰ)2.3幂函数课件新人教A版必修1:42张PPT
文档属性
| 名称 | 2019_2020学年高中数学第二章基本初等函数(Ⅰ)2.3幂函数课件新人教A版必修1:42张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 12:53:11 | ||
图片预览











文档简介
课件42张PPT。2.3 幂函数[目标导航]新知导学·素养养成1.幂函数的概念
一般地,函数 叫做幂函数,其中 是自变量, 是常数.y=xαxα思考1:幂函数图象不可能出现在第几象限?
答案:第四象限.这是因为y=xα中当x>0时,y不可能小于0.
思考2:两个幂函数图象最多有几个交点?最少呢?
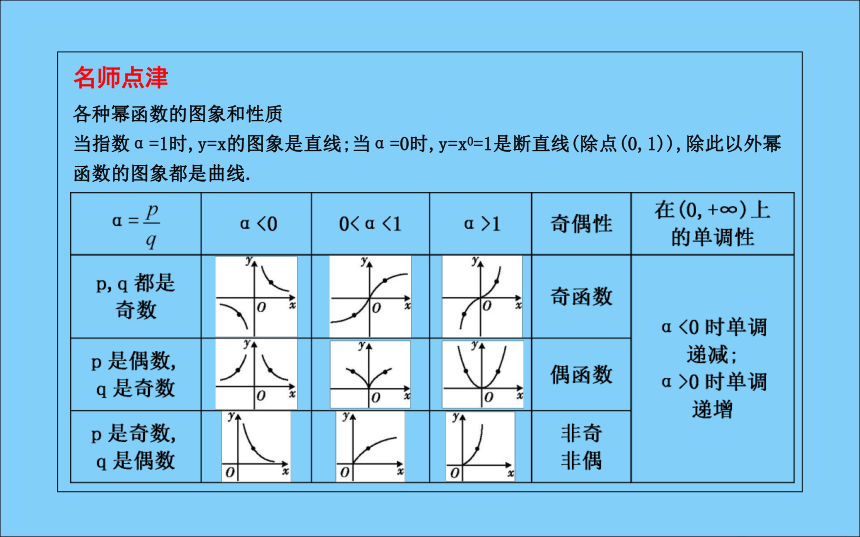
答案:两个幂函数图象最多有3个交点,如y=x3和y=x的图象,由于幂函数图象都过点(1,1),因此两幂函数图象最少有一个交点.3.幂函数的性质增减增增减名师点津各种幂函数的图象和性质
当指数α=1时,y=x的图象是直线;当α=0时,y=x0=1是断直线(除点(0,1)),除此以外幂函数的图象都是曲线.幂函数y=xα的图象在第一象限内具有如下特征:直线x=1,y=1,y=x将直角坐标平面在第一象限的直线x=1的右侧分为三个区域Ⅰ、Ⅱ、Ⅲ,如图.
则α∈(1,+∞)?y=xα的图象经过区域Ⅰ内;
α∈(0,1)?y=xα的图象经过区域Ⅱ内;
α∈(-∞,0)?y=xα的图象经过区域Ⅲ内.
并且在直线x=1的右侧,从x轴起,幂函数y=xα的指数α由小到大递增,即“指大图高”“指小图低”,在直线x=1的左侧,图象从下到上,相应的指数由大变小.课堂探究·素养提升解析:(2)幂函数f(x)=(m2-m-1)xm的图象与坐标轴无交点,可得m2-m-1=1,且m≤0,解得m=-1,则函数f(x)=x-1,所以函数是奇函数,在定义域上不是减函数,且无最值,故选B.(2)(2018·福建龙岩期中)若函数f(x)=(m2-m-1)xm是幂函数,且图象与坐标轴无交点,则f(x)( )
(A)是偶函数 (B)是奇函数
(C)是单调递减函数 (D)在定义域内有最小值易错警示(1)幂函数解析式的结构特征:①解析式是单项式;②幂指数为常数,底数为自变量,系数为1.
(2)幂函数y=xα的图象与坐标轴无交点,则α≤0,而不是α<0.解析:由m2-m-1=1得m=2或m=-1,
又x∈(0,+∞)时幂函数为减函数,
则需m2-2m-3<0,
所以m=-1舍去.故m=2.答案:2答案:(1)B 解析:(1)②⑦为指数函数,③中系数不是1,④中解析式为多项式,⑤中底数不是自变量本身,所以只有①⑥是幂函数,故选B.答案:(2)3(2)若四个幂函数y=xa,y=xb,y=xc,y=xd在同一坐标系中的图象如图,则a,b,c,d的大小关系是( )
(A)d>c>b>a
(B)a>b>c>d
(C)d>c>a>b
(D)a>b>d>c解析:(2)在第一象限内,x=1的右侧部分的图象,图象由下至上,幂指数增大,所以a>b>c>d.故选B.方法技巧(1)根据幂函数解析式选择幂函数图象应根据函数解析式的特征判断函数在第一象限时函数图象的变化趋势,再结合函数的定义域、奇偶性等方面确定函数图象的形状.
(2)根据幂函数的图象比较指数的大小,可根据幂函数的单调性以及图象的变化判断,也可利用特征,如令 x=2,作出直线x=2与各图象的交点,由指数函数y=2x的单调性即可由交点的纵坐标确定指数的大小关系.(2)如图是幂函数y=xm与y=xn在第一象限内的图象,则( )
(A)-1(B)n<-1,0(C)-11
(D)n<-1,m>1解析:(2)在(0,1)内取x0,作直线x=x0,
与各图象有交点,则“点低指数大”.
如图.0答案:(3)③方法技巧比较幂值的大小,关键在于构造适当的函数,若指数相同而底数不同,则考虑幂函数;若指数不同底数相同,则考虑指数函数;若底数不同,指数也不同,需引入中间量,利用幂函数与指数函数的单调性,也可以借助幂函数与指数函数的图象.题型四 易错辨析
[例4] 若(x+1)-2>(3-2x)-2,求x的范围.纠错:错解中只考虑了利用幂函数性质转化为关于x的不等式,而忽视了x+1≠0及3-2x≠0.学霸经验分享区(1)对于幂函数y=xα(α∈R),只要求出α的值就可以求出幂函数的解析式,求幂函数解析式的常用方法是待定系数法.
(2)求解幂函数图象问题的两种方法
①依据图象高低判断幂指数大小,相关结论为:在(0,1)上,指数越大,幂函数图象越靠近x轴(简记为指大图低);在(1,+∞)上,指数越大,幂函数图象越远离x轴(简记为指大图高).(3)幂式值大小比较应根据待比较幂式的特征,构造幂函数或指数函数性质比较其大小.
(4)对于幂函数的综合应用问题应注意以下两点:
①充分利用幂函数的性质,如单调性、奇偶性.
②注意分类讨论、数形结合思想的应用.课堂达标CB解析:y=x1,y=x3的定义域为R,且为奇函数,因此选B.BA5.不论α取何值,当x>0时,函数y=xα+5必过定点 .?解析:由于y=xα过点(1,1),因此y=xα+5过点(1,6).
答案:(1,6)
一般地,函数 叫做幂函数,其中 是自变量, 是常数.y=xαxα思考1:幂函数图象不可能出现在第几象限?
答案:第四象限.这是因为y=xα中当x>0时,y不可能小于0.
思考2:两个幂函数图象最多有几个交点?最少呢?
答案:两个幂函数图象最多有3个交点,如y=x3和y=x的图象,由于幂函数图象都过点(1,1),因此两幂函数图象最少有一个交点.3.幂函数的性质增减增增减名师点津各种幂函数的图象和性质
当指数α=1时,y=x的图象是直线;当α=0时,y=x0=1是断直线(除点(0,1)),除此以外幂函数的图象都是曲线.幂函数y=xα的图象在第一象限内具有如下特征:直线x=1,y=1,y=x将直角坐标平面在第一象限的直线x=1的右侧分为三个区域Ⅰ、Ⅱ、Ⅲ,如图.
则α∈(1,+∞)?y=xα的图象经过区域Ⅰ内;
α∈(0,1)?y=xα的图象经过区域Ⅱ内;
α∈(-∞,0)?y=xα的图象经过区域Ⅲ内.
并且在直线x=1的右侧,从x轴起,幂函数y=xα的指数α由小到大递增,即“指大图高”“指小图低”,在直线x=1的左侧,图象从下到上,相应的指数由大变小.课堂探究·素养提升解析:(2)幂函数f(x)=(m2-m-1)xm的图象与坐标轴无交点,可得m2-m-1=1,且m≤0,解得m=-1,则函数f(x)=x-1,所以函数是奇函数,在定义域上不是减函数,且无最值,故选B.(2)(2018·福建龙岩期中)若函数f(x)=(m2-m-1)xm是幂函数,且图象与坐标轴无交点,则f(x)( )
(A)是偶函数 (B)是奇函数
(C)是单调递减函数 (D)在定义域内有最小值易错警示(1)幂函数解析式的结构特征:①解析式是单项式;②幂指数为常数,底数为自变量,系数为1.
(2)幂函数y=xα的图象与坐标轴无交点,则α≤0,而不是α<0.解析:由m2-m-1=1得m=2或m=-1,
又x∈(0,+∞)时幂函数为减函数,
则需m2-2m-3<0,
所以m=-1舍去.故m=2.答案:2答案:(1)B 解析:(1)②⑦为指数函数,③中系数不是1,④中解析式为多项式,⑤中底数不是自变量本身,所以只有①⑥是幂函数,故选B.答案:(2)3(2)若四个幂函数y=xa,y=xb,y=xc,y=xd在同一坐标系中的图象如图,则a,b,c,d的大小关系是( )
(A)d>c>b>a
(B)a>b>c>d
(C)d>c>a>b
(D)a>b>d>c解析:(2)在第一象限内,x=1的右侧部分的图象,图象由下至上,幂指数增大,所以a>b>c>d.故选B.方法技巧(1)根据幂函数解析式选择幂函数图象应根据函数解析式的特征判断函数在第一象限时函数图象的变化趋势,再结合函数的定义域、奇偶性等方面确定函数图象的形状.
(2)根据幂函数的图象比较指数的大小,可根据幂函数的单调性以及图象的变化判断,也可利用特征,如令 x=2,作出直线x=2与各图象的交点,由指数函数y=2x的单调性即可由交点的纵坐标确定指数的大小关系.(2)如图是幂函数y=xm与y=xn在第一象限内的图象,则( )
(A)-1
(D)n<-1,m>1解析:(2)在(0,1)内取x0,作直线x=x0,
与各图象有交点,则“点低指数大”.
如图.0
[例4] 若(x+1)-2>(3-2x)-2,求x的范围.纠错:错解中只考虑了利用幂函数性质转化为关于x的不等式,而忽视了x+1≠0及3-2x≠0.学霸经验分享区(1)对于幂函数y=xα(α∈R),只要求出α的值就可以求出幂函数的解析式,求幂函数解析式的常用方法是待定系数法.
(2)求解幂函数图象问题的两种方法
①依据图象高低判断幂指数大小,相关结论为:在(0,1)上,指数越大,幂函数图象越靠近x轴(简记为指大图低);在(1,+∞)上,指数越大,幂函数图象越远离x轴(简记为指大图高).(3)幂式值大小比较应根据待比较幂式的特征,构造幂函数或指数函数性质比较其大小.
(4)对于幂函数的综合应用问题应注意以下两点:
①充分利用幂函数的性质,如单调性、奇偶性.
②注意分类讨论、数形结合思想的应用.课堂达标CB解析:y=x1,y=x3的定义域为R,且为奇函数,因此选B.BA5.不论α取何值,当x>0时,函数y=xα+5必过定点 .?解析:由于y=xα过点(1,1),因此y=xα+5过点(1,6).
答案:(1,6)
