2019_2020学年高中数学第二章基本初等函数(Ⅰ)章末总结课件新人教A版必修1:23张PPT
文档属性
| 名称 | 2019_2020学年高中数学第二章基本初等函数(Ⅰ)章末总结课件新人教A版必修1:23张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 685.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 12:53:32 | ||
图片预览



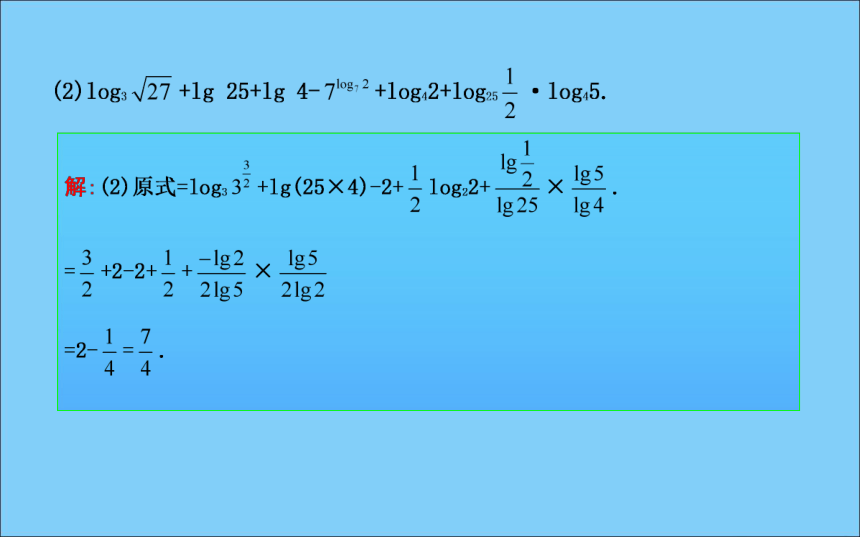



文档简介
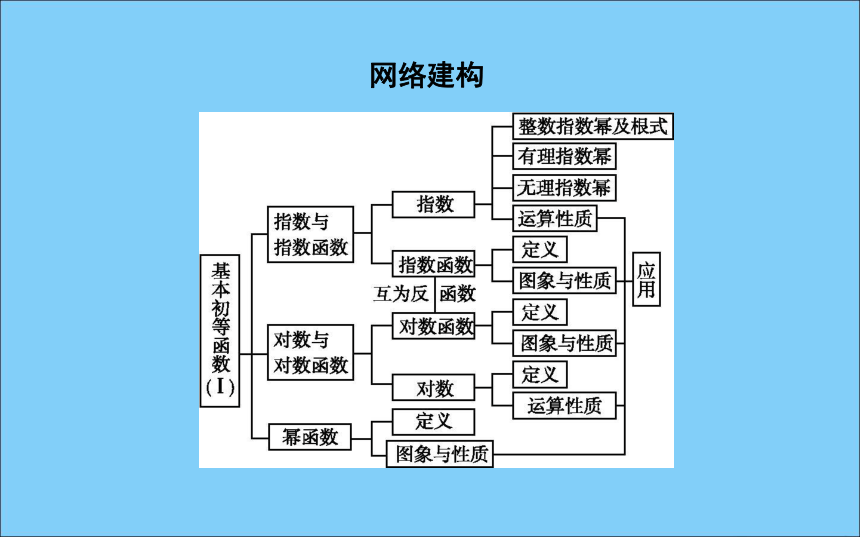
课件23张PPT。章末总结网络建构知识辨析判断下列说法是否正确(请在括号中填“√”或“×”)×2.指数函数的图象一定在x轴的上方.( )
3.y=3·2x是指数函数.( )
4.任何指数式都可以化为对数式.( )
5.loga(xy)=logax+logay(a>0且a≠1).( )
6.y=x2与y=log2x互为反函数.( )
7.互为反函数的两个函数图象关于y=x对称.( )
8.幂函数图象可在直角坐标系第四象限出现.( )
9.对数函数图象一定在y轴右侧.( )√××××√×√题型归纳·素养提升规律方法(1)指数式的运算:注意化简顺序,一般负指数先转化成正指数,根式化为分数指数幂运算.
(2)对数式的运算:①注意公式应用过程中范围的变化,前后要等价.②熟练地运用对数的三个运算性质并结合对数恒等式,换底公式是对数计算、化简、证明常用的技巧.题型二 指数函数、对数函数、幂函数的图象和性质
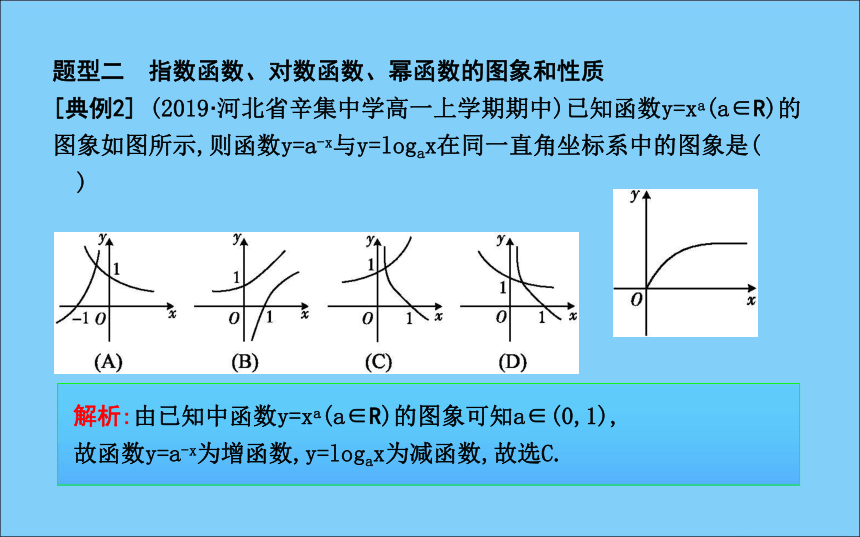
[典例2] (2019·河北省辛集中学高一上学期期中)已知函数y=xa(a∈R)的图象如图所示,则函数y=a-x与y=logax在同一直角坐标系中的图象是( )解析:由已知中函数y=xa(a∈R)的图象可知a∈(0,1),
故函数y=a-x为增函数,y=logax为减函数,故选C.规律方法求解与三种函数图象有关的问题,首先应根据函数解析式的特征,从函数的定义域、值域、单调性等性质分析,再结合三种函数图象所过定点等判断函数图象的形状.[典例3] (1)(2019·内蒙古鄂尔多斯高一上期中)若a=20.5,b=logπ3,c= log20.5,则( )
(A)b>a>c (B)a>b>c (C)c>a>b (D)b>c>a
(2)(2018·广东佛山高一检测)设a=0.60.6,b=0.61.5,c=1.50.6,则a,b,c的大小关系是( )
(A)a20=1,根据对数函数的单调性可得0=logπ1b>c,故选B.
(2)由y=0.6x在(0,+∞)上为减函数知0<0.61.5<0.60.6<0.60=1,即b又y=x0.6在(0,+∞)上为增函数知1.50.6>0.60.6,
即c>a,故b(A)a(C)a(2)当两个数都是指数幂或对数式时,可将其看成某个指数函数、对数函数或幂函数的函数值,然后利用该函数的单调性比较.
(3)比较多个数的大小时,先利用“0”“1”作为分界点,然后在各部分内再利用函数性质比较大小.[典例5] (2019·山东师范大学附属中学高一上期中)设0(A)(-∞,0) (B)(loga3,+∞)
(C)(-∞,loga3) (D)(0,+∞)解析:由题意,令t=ax,则y=loga(t2-2t-2),
若使f(x)<0,即y=loga(t2-2t-2)<0,
由对数函数的性质知,01,
解得t>3或t<-1,
又因为t=ax时t>0,
故其解为t>3,即ax>3,
又有0(A)y=ln(1-x) (B)y=ln(2-x)
(C)y=ln(1+x) (D)y=ln(2+x)4.(2018·全国Ⅲ卷)设a=log0.20.3,b=log20.3,则( )
(A)a+b(C)a+b<0(A)2x<3y<5z (B)5z<2x<3y
(C)3y<5z<2x (D)3y<2x<5zD
3.y=3·2x是指数函数.( )
4.任何指数式都可以化为对数式.( )
5.loga(xy)=logax+logay(a>0且a≠1).( )
6.y=x2与y=log2x互为反函数.( )
7.互为反函数的两个函数图象关于y=x对称.( )
8.幂函数图象可在直角坐标系第四象限出现.( )
9.对数函数图象一定在y轴右侧.( )√××××√×√题型归纳·素养提升规律方法(1)指数式的运算:注意化简顺序,一般负指数先转化成正指数,根式化为分数指数幂运算.
(2)对数式的运算:①注意公式应用过程中范围的变化,前后要等价.②熟练地运用对数的三个运算性质并结合对数恒等式,换底公式是对数计算、化简、证明常用的技巧.题型二 指数函数、对数函数、幂函数的图象和性质
[典例2] (2019·河北省辛集中学高一上学期期中)已知函数y=xa(a∈R)的图象如图所示,则函数y=a-x与y=logax在同一直角坐标系中的图象是( )解析:由已知中函数y=xa(a∈R)的图象可知a∈(0,1),
故函数y=a-x为增函数,y=logax为减函数,故选C.规律方法求解与三种函数图象有关的问题,首先应根据函数解析式的特征,从函数的定义域、值域、单调性等性质分析,再结合三种函数图象所过定点等判断函数图象的形状.[典例3] (1)(2019·内蒙古鄂尔多斯高一上期中)若a=20.5,b=logπ3,c= log20.5,则( )
(A)b>a>c (B)a>b>c (C)c>a>b (D)b>c>a
(2)(2018·广东佛山高一检测)设a=0.60.6,b=0.61.5,c=1.50.6,则a,b,c的大小关系是( )
(A)a
(2)由y=0.6x在(0,+∞)上为减函数知0<0.61.5<0.60.6<0.60=1,即b
即c>a,故b
(3)比较多个数的大小时,先利用“0”“1”作为分界点,然后在各部分内再利用函数性质比较大小.[典例5] (2019·山东师范大学附属中学高一上期中)设0
(C)(-∞,loga3) (D)(0,+∞)解析:由题意,令t=ax,则y=loga(t2-2t-2),
若使f(x)<0,即y=loga(t2-2t-2)<0,
由对数函数的性质知,0
解得t>3或t<-1,
又因为t=ax时t>0,
故其解为t>3,即ax>3,
又有0
(C)y=ln(1+x) (D)y=ln(2+x)4.(2018·全国Ⅲ卷)设a=log0.20.3,b=log20.3,则( )
(A)a+b
(C)3y<5z<2x (D)3y<2x<5zD
