2019_2020学年高中数学第三章函数的应用3.1.1方程的根与函数的零点课件新人教A版必修1:35张PPT
文档属性
| 名称 | 2019_2020学年高中数学第三章函数的应用3.1.1方程的根与函数的零点课件新人教A版必修1:35张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 790.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 12:51:49 | ||
图片预览











文档简介
课件35张PPT。第三章 函数的应用
3.1 函数与方程
3.1.1 方程的根与函数的零点[目标导航]新知导学·素养养成1.函数的零点
对于函数y=f(x),把使 叫做函数y=f(x)的零点.f(x)=0的实数x2.方程、函数、图象之间的关系
方程f(x)=0 ?函数y=f(x)的图象与x轴有交点?函数y=f(x) .有实数根有零点思考1:方程的根与对应的函数图象有什么关系?
答案:方程的根就是对应函数图象与x轴交点的横坐标.3.函数零点的存在条件
如果函数y=f(x)在区间[a,b]上的图象是 的一条曲线,并且有 ,那么,函数y=f(x)在区间(a,b)内 ,即存在c∈(a,b),使得 ,这个c也就是方程f(x)=0的根.连续不断f(a)·f(b)<0有零点f(c)=0思考2:函数y=f(x)在[a,b]上连续不间断,当f(a)f(b)<0时,函数零点个数是否唯一?
答案:不唯一.只有函数y=f(x)在区间[a,b]上是单调函数时函数零点 唯一.名师点津(1)函数F(x)=f(x)-g(x)的零点就是方程f(x)=g(x)的实数根,也是函数y=f(x)的图象与函数y=g(x)的图象交点的横坐标.
(2)常见函数的零点
①二次函数的零点
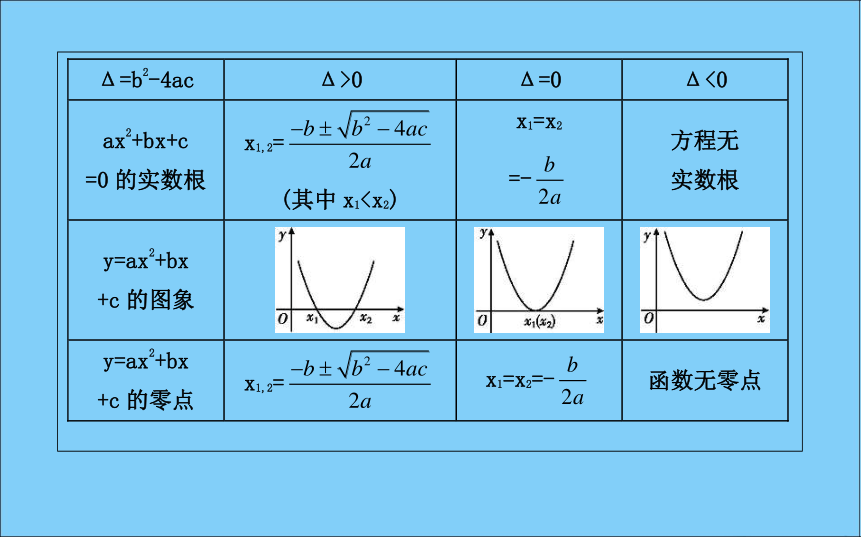
当a>0时,一元二次方程ax2+bx+c=0的实数根、二次函数y=ax2+bx+c的图象与二次函数y=ax2+bx+c的零点之间的关系如下表所示:类似可得当a<0时的情形.
②正比例函数y=kx(k≠0)仅有一个零点0.⑤指数函数y=ax(a>0,且a≠1)没有零点.
⑥对数函数y=logax(a>0,且a≠1)仅有一个零点1.
⑦幂函数y=xn,当n>0时,仅有一个零点0;当n≤0时,没有零点.课堂探究·素养提升(2)已知函数f(x)=ax-b(a≠0)的零点为3,求函数g(x)=bx2+ax的零点.方法技巧(1)求函数f(x)的零点就是求方程f(x)=0的解,求解时注意函数的定义域.
(2)已知x0是函数f(x)的零点,则必有f(x0)=0.(2)令x2+2x+4=0,由于Δ=22-4×4=-12<0,
所以方程x2+2x+4=0无解,
所以函数f(x)=x2+2x+4不存在零点.解:(3)令2x-3=0,解得x=log23,
所以函数f(x)=2x-3的零点是log23.(3)f(x)=2x-3;(4)f(x)=1-log3x.(4)令1-log3x=0,解得x=3,
所以函数f(x)=1-log3x的零点是3.(1)解析:由奇函数性质知f(-3)=-f(3)=0,故3与-3均为函数的零点,又f(0)=0,因此函数y=f(x)的零点有3个,分别为-3,0,3.[备用例1] (1)若函数y=f(x)为定义在R上的奇函数,当x∈(-∞,0)时函数为减函数,且f(-3)=0,则函数f(x)的零点构成的集合有 个元素.?答案:3(2)解:①因为x3-x2+x-1=x2(x-1)+(x-1)=(x-1)(x2+1)=0.
所以x=1,即f(x)的零点是1.(2)求下列函数的零点:
①f(x)=x3-x2+x-1;
②f(x)=x4-2x2-3.(3)讨论函数y=(ax-1)(x-2)(x∈R)的零点.方法技巧判断函数零点的个数的方法
(1)直接求出函数的零点进行判断,即转化为方程f(x)=0解的个数.
(2)结合函数图象进行判断,即转化为函数图象与x轴交点个数或两个函数图象交点的个数,此法常用于函数解析式中含指数、对数、幂函数的式子.
(3)借助函数的单调性进行判断.[备用例2] (1)函数f(x)=|x-2|-ln x在定义域内零点的个数为( )
(A)0 (B)1 (C)2 (D)3解析:(1)由题意,函数f(x)的定义域为(0,+∞).
由函数零点的定义,f(x)在(0,+∞)内的零点即是方程|x-2|-ln x=0 的根.
令y1=|x-2|,y2=ln x(x>0),在一个坐标系中画出两个函数的图象.
由图得,两个函数图象有两个交点,故方程有两个根,即对应函数有两个零点.
故选C.(2)关于函数f(x)=3x+x2+2x-1的零点,下列说法中正确的是( )
(A)函数有两个正数零点
(B)函数有两个负数零点
(C)函数有两个零点,一个是正数,另一个是零
(D)函数有两个零点,一个是负数,另一个是零解析:(2)令f(x)=0,得3x+x2+2x-1=0,即3x=-x2-2x+1.在同一直角坐标系内作出函数y=3x和y=-x2-2x+1的图象如图,可知两个函数图象有两个交点,因此函数f(x)=3x+x2+2x-1有两个零点,其中一个是负数,另一个是零.故选D.题型三 函数零点所在区间
[例3] (1)(2019·江苏徐州市高一上期中)函数f(x)=2x+3x的零点所在的区间是( )
(A)(-2,-1) (B)(-1,0)
(C)(0,1) (D)(1,2)解析:(1)因为y=2x,y=3x在R上是增函数,
所以f(x)=2x+3x在R上是增函数,
而f(-2)=2-2-6<0,
f(-1)=2-1-3<0,f(0)=20=1>0,
f(1)=2+3=5>0,f(2)=22+6=10>0,
所以f(-1)·f(0)<0,故函数f(x)在区间(-1,0)上有零点,故选B.方法技巧(1)确定函数的零点所在的区间时,通常利用零点存在性定理,转化为判断区间端点对应的函数值的符号是否相反.使用该定理的前提条件是函数连续不间断且严格单调.
(2)求方程f(x)=g(x)的根所在的区间,可利用构造函数的方法构造函数h(x)=f(x)-g(x),通过判断函数h(x)零点所在的区间转化为方程f(x)=g(x)的根所在的区间.即时训练3-1:(1)根据表格中的数据,可以判定函数f(x)=ln x-x+2有一个零点所在的区间为(k,k+1)(k∈N+),则k的值为( ) (A)3 (B)4 (C)5 (D)6解析:(1)由题意得f(1)=ln 1-1+2=1>0.f(2)=ln 2-2+2=ln 2=0.69>0.
f(3)=ln 3-3+2=ln 3-1=1.10-1=0.10>0.f(4)=ln 4-4+2=1.39-2=-0.61
<0.f(5)=ln 5-5+2=1.61-3=-1.39<0.
由f(3)·f(4)<0知零点所在区间为(3,4),故选A.
答案:(1)A(2)若函数f(x)=x2-16x+m+3在区间[-1,1]上存在零点,则实数m的取值范围是 .?解析:(2)因为f(x)=x2-16x+m+3在[-1,1]上严格单调,
所以f(-1)·f(1)≤0.
解得-20≤m≤12.
答案:(2)[-20,12]错解:因为f(-1)=-(-1)2-3=-4,f(1)=1+3=4.
所以f(-1)·f(1)<0.所以函数f(x)在[-1,1]上存在零点.
纠错:由于函数f(x)在[-1,1]上的图象不连续,故不能使用函数零点存在性定理判断函数的零点.
正解:当x≥0时,令f(x)=x2+3=0可知,方程无解,
当x<0时,令f(x)=-x2-3=0可知,方程无解.
即函数f(x)在[-1,1]上无零点.学霸经验分享区(1)函数的零点不是一个点而是函数图象与x轴交点的横坐标,也就是函数解析式对应方程的根,求函数的零点常转化为求函数对应方程的根,而判断函数零点或确定函数零点个数,常用数形结合或函数零点的存在性定理.
(2)函数零点的存在性定理的使用条件是函数图象连续不间断,应注意函数零点的存在性定理只能判断零点存在而不能确定零点个数.
(3)函数与方程有着密切的联系,有些方程问题可以转化为函数问题求解,同样,函数问题也可转化为方程问题,这正是函数与方程思想的基础.课堂达标解析:由函数零点的意义可得,函数的零点是否存在表现在函数图象与x轴有无交点.故选A.1.下列图象表示的函数中没有零点的是( )AD3.已知函数f(x)在区间[a,b]上单调,且图象是连续不断的,若f(a)·f(b) <0,则方程f(x)=0在区间[a,b]上( )
(A)至少有一实数根 (B)至多有一实数根
(C)没有实数根 (D)必有唯一的实数根D解析:由题意知函数f(x)为连续函数,因为f(a)·f(b)<0,
所以函数f(x)在区间[a,b]上至少有一个零点.
又因为函数f(x)在区间[a,b]上是单调函数,
所以函数f(x)在区间[a,b]上至多有一个零点,故函数f(x)在区间[a,b]上有且只有一个零点,即方程f(x)=0在区间[a,b]内必有唯一的实数根,故选D.4.(2019·福建省福州市八县一中高一上期中)设x0是函数f(x)=ln x+x-4的零点,则x0所在的区间为( )
(A)(0,1) (B)(1,2)
(C)(2,3) (D)(3,4)C解析:因为f(2)=ln 2+2-4=ln 2-2<0,f(3)=ln 3+3-4=ln 3-1>0,
所以函数f(x)=ln x+x-4的零点x0∈(2,3),故选C.答案:0
3.1 函数与方程
3.1.1 方程的根与函数的零点[目标导航]新知导学·素养养成1.函数的零点
对于函数y=f(x),把使 叫做函数y=f(x)的零点.f(x)=0的实数x2.方程、函数、图象之间的关系
方程f(x)=0 ?函数y=f(x)的图象与x轴有交点?函数y=f(x) .有实数根有零点思考1:方程的根与对应的函数图象有什么关系?
答案:方程的根就是对应函数图象与x轴交点的横坐标.3.函数零点的存在条件
如果函数y=f(x)在区间[a,b]上的图象是 的一条曲线,并且有 ,那么,函数y=f(x)在区间(a,b)内 ,即存在c∈(a,b),使得 ,这个c也就是方程f(x)=0的根.连续不断f(a)·f(b)<0有零点f(c)=0思考2:函数y=f(x)在[a,b]上连续不间断,当f(a)f(b)<0时,函数零点个数是否唯一?
答案:不唯一.只有函数y=f(x)在区间[a,b]上是单调函数时函数零点 唯一.名师点津(1)函数F(x)=f(x)-g(x)的零点就是方程f(x)=g(x)的实数根,也是函数y=f(x)的图象与函数y=g(x)的图象交点的横坐标.
(2)常见函数的零点
①二次函数的零点
当a>0时,一元二次方程ax2+bx+c=0的实数根、二次函数y=ax2+bx+c的图象与二次函数y=ax2+bx+c的零点之间的关系如下表所示:类似可得当a<0时的情形.
②正比例函数y=kx(k≠0)仅有一个零点0.⑤指数函数y=ax(a>0,且a≠1)没有零点.
⑥对数函数y=logax(a>0,且a≠1)仅有一个零点1.
⑦幂函数y=xn,当n>0时,仅有一个零点0;当n≤0时,没有零点.课堂探究·素养提升(2)已知函数f(x)=ax-b(a≠0)的零点为3,求函数g(x)=bx2+ax的零点.方法技巧(1)求函数f(x)的零点就是求方程f(x)=0的解,求解时注意函数的定义域.
(2)已知x0是函数f(x)的零点,则必有f(x0)=0.(2)令x2+2x+4=0,由于Δ=22-4×4=-12<0,
所以方程x2+2x+4=0无解,
所以函数f(x)=x2+2x+4不存在零点.解:(3)令2x-3=0,解得x=log23,
所以函数f(x)=2x-3的零点是log23.(3)f(x)=2x-3;(4)f(x)=1-log3x.(4)令1-log3x=0,解得x=3,
所以函数f(x)=1-log3x的零点是3.(1)解析:由奇函数性质知f(-3)=-f(3)=0,故3与-3均为函数的零点,又f(0)=0,因此函数y=f(x)的零点有3个,分别为-3,0,3.[备用例1] (1)若函数y=f(x)为定义在R上的奇函数,当x∈(-∞,0)时函数为减函数,且f(-3)=0,则函数f(x)的零点构成的集合有 个元素.?答案:3(2)解:①因为x3-x2+x-1=x2(x-1)+(x-1)=(x-1)(x2+1)=0.
所以x=1,即f(x)的零点是1.(2)求下列函数的零点:
①f(x)=x3-x2+x-1;
②f(x)=x4-2x2-3.(3)讨论函数y=(ax-1)(x-2)(x∈R)的零点.方法技巧判断函数零点的个数的方法
(1)直接求出函数的零点进行判断,即转化为方程f(x)=0解的个数.
(2)结合函数图象进行判断,即转化为函数图象与x轴交点个数或两个函数图象交点的个数,此法常用于函数解析式中含指数、对数、幂函数的式子.
(3)借助函数的单调性进行判断.[备用例2] (1)函数f(x)=|x-2|-ln x在定义域内零点的个数为( )
(A)0 (B)1 (C)2 (D)3解析:(1)由题意,函数f(x)的定义域为(0,+∞).
由函数零点的定义,f(x)在(0,+∞)内的零点即是方程|x-2|-ln x=0 的根.
令y1=|x-2|,y2=ln x(x>0),在一个坐标系中画出两个函数的图象.
由图得,两个函数图象有两个交点,故方程有两个根,即对应函数有两个零点.
故选C.(2)关于函数f(x)=3x+x2+2x-1的零点,下列说法中正确的是( )
(A)函数有两个正数零点
(B)函数有两个负数零点
(C)函数有两个零点,一个是正数,另一个是零
(D)函数有两个零点,一个是负数,另一个是零解析:(2)令f(x)=0,得3x+x2+2x-1=0,即3x=-x2-2x+1.在同一直角坐标系内作出函数y=3x和y=-x2-2x+1的图象如图,可知两个函数图象有两个交点,因此函数f(x)=3x+x2+2x-1有两个零点,其中一个是负数,另一个是零.故选D.题型三 函数零点所在区间
[例3] (1)(2019·江苏徐州市高一上期中)函数f(x)=2x+3x的零点所在的区间是( )
(A)(-2,-1) (B)(-1,0)
(C)(0,1) (D)(1,2)解析:(1)因为y=2x,y=3x在R上是增函数,
所以f(x)=2x+3x在R上是增函数,
而f(-2)=2-2-6<0,
f(-1)=2-1-3<0,f(0)=20=1>0,
f(1)=2+3=5>0,f(2)=22+6=10>0,
所以f(-1)·f(0)<0,故函数f(x)在区间(-1,0)上有零点,故选B.方法技巧(1)确定函数的零点所在的区间时,通常利用零点存在性定理,转化为判断区间端点对应的函数值的符号是否相反.使用该定理的前提条件是函数连续不间断且严格单调.
(2)求方程f(x)=g(x)的根所在的区间,可利用构造函数的方法构造函数h(x)=f(x)-g(x),通过判断函数h(x)零点所在的区间转化为方程f(x)=g(x)的根所在的区间.即时训练3-1:(1)根据表格中的数据,可以判定函数f(x)=ln x-x+2有一个零点所在的区间为(k,k+1)(k∈N+),则k的值为( ) (A)3 (B)4 (C)5 (D)6解析:(1)由题意得f(1)=ln 1-1+2=1>0.f(2)=ln 2-2+2=ln 2=0.69>0.
f(3)=ln 3-3+2=ln 3-1=1.10-1=0.10>0.f(4)=ln 4-4+2=1.39-2=-0.61
<0.f(5)=ln 5-5+2=1.61-3=-1.39<0.
由f(3)·f(4)<0知零点所在区间为(3,4),故选A.
答案:(1)A(2)若函数f(x)=x2-16x+m+3在区间[-1,1]上存在零点,则实数m的取值范围是 .?解析:(2)因为f(x)=x2-16x+m+3在[-1,1]上严格单调,
所以f(-1)·f(1)≤0.
解得-20≤m≤12.
答案:(2)[-20,12]错解:因为f(-1)=-(-1)2-3=-4,f(1)=1+3=4.
所以f(-1)·f(1)<0.所以函数f(x)在[-1,1]上存在零点.
纠错:由于函数f(x)在[-1,1]上的图象不连续,故不能使用函数零点存在性定理判断函数的零点.
正解:当x≥0时,令f(x)=x2+3=0可知,方程无解,
当x<0时,令f(x)=-x2-3=0可知,方程无解.
即函数f(x)在[-1,1]上无零点.学霸经验分享区(1)函数的零点不是一个点而是函数图象与x轴交点的横坐标,也就是函数解析式对应方程的根,求函数的零点常转化为求函数对应方程的根,而判断函数零点或确定函数零点个数,常用数形结合或函数零点的存在性定理.
(2)函数零点的存在性定理的使用条件是函数图象连续不间断,应注意函数零点的存在性定理只能判断零点存在而不能确定零点个数.
(3)函数与方程有着密切的联系,有些方程问题可以转化为函数问题求解,同样,函数问题也可转化为方程问题,这正是函数与方程思想的基础.课堂达标解析:由函数零点的意义可得,函数的零点是否存在表现在函数图象与x轴有无交点.故选A.1.下列图象表示的函数中没有零点的是( )AD3.已知函数f(x)在区间[a,b]上单调,且图象是连续不断的,若f(a)·f(b) <0,则方程f(x)=0在区间[a,b]上( )
(A)至少有一实数根 (B)至多有一实数根
(C)没有实数根 (D)必有唯一的实数根D解析:由题意知函数f(x)为连续函数,因为f(a)·f(b)<0,
所以函数f(x)在区间[a,b]上至少有一个零点.
又因为函数f(x)在区间[a,b]上是单调函数,
所以函数f(x)在区间[a,b]上至多有一个零点,故函数f(x)在区间[a,b]上有且只有一个零点,即方程f(x)=0在区间[a,b]内必有唯一的实数根,故选D.4.(2019·福建省福州市八县一中高一上期中)设x0是函数f(x)=ln x+x-4的零点,则x0所在的区间为( )
(A)(0,1) (B)(1,2)
(C)(2,3) (D)(3,4)C解析:因为f(2)=ln 2+2-4=ln 2-2<0,f(3)=ln 3+3-4=ln 3-1>0,
所以函数f(x)=ln x+x-4的零点x0∈(2,3),故选C.答案:0
