2019_2020学年高中数学第三章函数的应用3.1.2用二分法求方程的近似解课件新人教A版必修1:28张PPT
文档属性
| 名称 | 2019_2020学年高中数学第三章函数的应用3.1.2用二分法求方程的近似解课件新人教A版必修1:28张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 344.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 00:00:00 | ||
图片预览







文档简介
课件28张PPT。3.1.2 用二分法求方程的近似解[目标导航]新知导学·素养养成1.二分法的定义
对于在区间[a,b]上 且 的函数y=f(x),通过不断地把函数f(x)的零点所在的区间 ,使区间的两个端点逐步逼近 ,进而得到零点近似值的方法叫做二分法.连续不断f(a)·f(b)<0一分为二零点思考:若函数y=f(x)在定义域内有零点,该零点是否一定能用二分法求解?答案:二分法只适用于函数的变号零点(即函数在零点两侧符号相反),因此函数在零点两侧同号的零点不能用二分法求解,如f(x)=(x-1)2的零点就不能用二分法求解.2.二分法的步骤
给定精确度ε,用二分法求函数f(x)零点近似值的步骤如下:
(1)确定区间[a,b],验证 ,给定精确度ε.(2)求区间(a,b)的中点c.
(3)计算f(c):
①若f(c)=0,则c就是函数的零点;
②若f(a)·f(c)<0,则令b=c(此时零点x0∈ );
③若f(c)·f(b)<0,则令a=c(此时零点x0∈ ).
(4)判断是否达到精确度ε:即若 ,则得到零点近似值a(或b);否则重复(2)~(4).f(a)·f(b)<0(a,c)(c,b)|a-b|<ε名师点津(1)变号零点与不变号零点
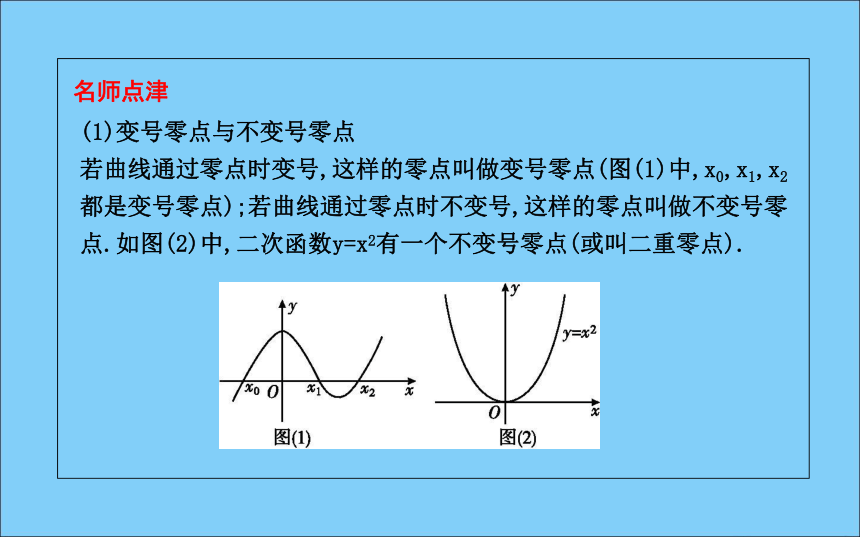
若曲线通过零点时变号,这样的零点叫做变号零点(图(1)中,x0,x1,x2都是变号零点);若曲线通过零点时不变号,这样的零点叫做不变号零点.如图(2)中,二次函数y=x2有一个不变号零点(或叫二重零点).(2)“精确度”与“精确到”
①精确度:近似数的误差不超过某个数,就说它的精确度是多少,即设x为准确值,x′为x的一个近似值,若|x′-x|<ε,则x′是精确度为ε的x的一个近似值,精确度简称精度.用二分法求方程的近似解时,只要根的存在区间(a,b)满足|a-b|<ε,两端点或区间内的任意一个数均可作为方程的近似解.②精确到:按四舍五入的原则得到准确值x的前几位近似值x′,x′的最后一位有效数字在某一数位,就说精确到某一数位.如:π=
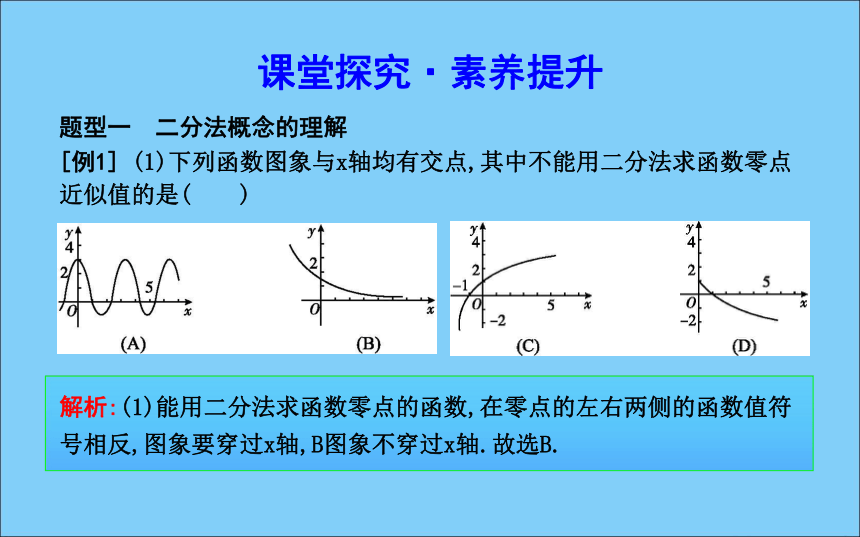
3.141 592 6…, 若取3位有效数字,则x′=3.14,精确到0.01(即百分位);若取5位有效数字,则x′=3.141 6,精确到0.000 1(即万分位).课堂探究·素养提升题型一 二分法概念的理解[例1] (1)下列函数图象与x轴均有交点,其中不能用二分法求函数零点近似值的是( )解析:(1)能用二分法求函数零点的函数,在零点的左右两侧的函数值符号相反,图象要穿过x轴,B图象不穿过x轴.故选B.解析:(2)因为第一次所取的区间是[-2,4],所以第二次所取的区间可能是[-2,1],[1,4],第三次所取的区间可能为[-2,-0.5],[-0.5,1],[1, 2.5],[2.5,4],故选D.(2)在用二分法求函数f(x)零点近似值时,第一次取的区间是[-2,4],则第三次所取的区间可能是( )
(A)[1,4] (B)[-2,1]
(C)[-2,2.5] (D)[-0.5,1]方法技巧(1)用二分法求函数的零点近似值的方法仅对函数的变号零点适用,即条件f(a)·f(b)<0是必不可少的,对函数的不变号零点不适用.(2)使用二分法确定零点所在区间的原则是取与区间端点的值异号的区间中点.即时训练1-1:(1)(2019·湖南岳阳一中阶段检测)用二分法求如图所示的图象所表示的函数f(x)的零点时,不可能求出的零点是( )
(A)x1 (B)x2
(C)x3 (D)x4解析:(1)观察题中图象可知,x3附近两边的函数值都为负值,所以x3不能用二分法求得,故选C.答案:(1)C(2)某同学在借助计算器求“方程lg x=2-x的近似解(精确度0.1)”时,设f(x)=lg x+x-2,算得f(1)<0,f(2)>0.在以下过程中,使用“二分法”又取了4个x的值,计算了其函数值的正负,并得出判断:方程的近似解为x=1.8,那么他所取的x的4个值中最后一个值是 .答案:(2)1.812 5 [备用例1] (1)若函数f(x)=x2-4x+t存在零点,但不能用二分法求解,则t= .?
(2)已知函数f(x)=x3-2x-5,f(2.5)>0,用二分法求方程x3-2x-5=0在区间(2,3)内的实根,取区间中点为x0=2.5,那么下一个有根的区间是 .解析:(1)由题意知函数f(x)=x2-4x+t与x轴只有一个交点,
故Δ=16-4t=0,则t=4.
(2)因为f(2)=23-2×2-5=-1<0,
f(2.5)>0,f(3)=33-2×3-5=16>0,
所以f(2)·f(2.5)<0,
所以方程x3-2x-5=0在(2,2.5)内有实根.
答案:(1)4 (2)(2,2.5)题型二 二分法的步骤[例2] 用二分法求方程f(x)=0在[0,4]上的近似解时,最多经过 次计算精确度可以达到0.001. 答案:12方法技巧即时训练2-1:若用二分法求函数f(x)在(a,b)内的唯一零点时,精确度为0.001,则结束计算的条件是 .题型三 用二分法求方程的近似解[例3] 用二分法求方程x3-x-1=0在区间(1,1.5)内的一个近似解(精确度0.1).(提示:1.53=3.375,1.253≈1.953,1.3753≈2.6,1.312 53≈2.261)解:设f(x)=x3-x-1,
因为f(1)=1-1-1=-1<0,
f(1.5)=3.375-1.5-1=0.875>0,
所以f(x)在区间(1,1.5)上存在零点.
取区间(1,1.5)作为初始区间,用二分法逐次计算列表如下:因为|1.375-1.312 5|=0.062 5<0.1,
故函数f(x)=x3-x-1在(1,1.5)内的一个近似零点为1.375.
即方程x3-x-1=0在(1,1.5)内的一个近似解为1.375.方法技巧使用二分法求方程的近似解应转化为求其相应函数的近似零点,当区间两个端点在满足精确度条件下的近似值相等时,所得区间两个端点的近似值便为所求方程的根(或函数零点).即时训练3-1:利用二分法求方程ln x=3-x的根(精确度为0.1)(以下数据可供参考:ln 2.5≈0.916 3,ln 2.25≈0.810 9,ln 2.125≈0.753 8,
ln 2.75≈1.011 6,ln 2.187 5≈0.782 8,ln 2.218 75≈0.796 9,
ln 2.471 25≈0.904 7).解:令f(x)=ln x+x-3.
因为f(2)=ln 2-1<0,f(3)=ln 3>0,
所以取(2,3)作为函数零点计算的初始区间,用二分法逐次计算,列表如下:因为|2.187 5-2.25|=0.0625<0.1.
故函数f(x)=ln x+x-3在(2,3)内的一个近似零点为2.25.
所以方程ln x=3-x在(2,3)内的一个近似根为2.25.学霸经验分享区(1)使用“二分法”时应注意以下两点:
①选好计算的初始区间,保证所选区间既要符合条件,又要使其长度
最短;②计算时要根据给定的精确度,检验计算所得的区间是否满足这一
条件.1.用二分法求函数f(x)=2x-3的零点时,初始区间可选为( )
(A)(-1,0) (B)(0,1)
(C)(2,3) (D)(1,2)课堂达标D解析:由f(0)=1-3=-2,f(1)=-1,f(2)=1知选D.2.通过下列函数的图象,判断不能用“二分法”求其零点的是( )
(A)①②③ (B)②③④
(C)①②④ (D)①③④C解析:能用二分法求零点的函数必须在给定区间[a,b]上连续不断,并且有f(a)·f(b)<0,由图象可得,只有③能满足此条件,故不能用“二分法”求其零点的是①②④,故选C.D 4.用“二分法”可求近似解,对于精确度ε说法正确的是( )
(A)ε越大,零点的精确度越高
(B)ε越大,零点的精确度越低
(C)重复计算次数就是ε
(D)重复计算次数与ε无关B答案:f(x)=x5-2
对于在区间[a,b]上 且 的函数y=f(x),通过不断地把函数f(x)的零点所在的区间 ,使区间的两个端点逐步逼近 ,进而得到零点近似值的方法叫做二分法.连续不断f(a)·f(b)<0一分为二零点思考:若函数y=f(x)在定义域内有零点,该零点是否一定能用二分法求解?答案:二分法只适用于函数的变号零点(即函数在零点两侧符号相反),因此函数在零点两侧同号的零点不能用二分法求解,如f(x)=(x-1)2的零点就不能用二分法求解.2.二分法的步骤
给定精确度ε,用二分法求函数f(x)零点近似值的步骤如下:
(1)确定区间[a,b],验证 ,给定精确度ε.(2)求区间(a,b)的中点c.
(3)计算f(c):
①若f(c)=0,则c就是函数的零点;
②若f(a)·f(c)<0,则令b=c(此时零点x0∈ );
③若f(c)·f(b)<0,则令a=c(此时零点x0∈ ).
(4)判断是否达到精确度ε:即若 ,则得到零点近似值a(或b);否则重复(2)~(4).f(a)·f(b)<0(a,c)(c,b)|a-b|<ε名师点津(1)变号零点与不变号零点
若曲线通过零点时变号,这样的零点叫做变号零点(图(1)中,x0,x1,x2都是变号零点);若曲线通过零点时不变号,这样的零点叫做不变号零点.如图(2)中,二次函数y=x2有一个不变号零点(或叫二重零点).(2)“精确度”与“精确到”
①精确度:近似数的误差不超过某个数,就说它的精确度是多少,即设x为准确值,x′为x的一个近似值,若|x′-x|<ε,则x′是精确度为ε的x的一个近似值,精确度简称精度.用二分法求方程的近似解时,只要根的存在区间(a,b)满足|a-b|<ε,两端点或区间内的任意一个数均可作为方程的近似解.②精确到:按四舍五入的原则得到准确值x的前几位近似值x′,x′的最后一位有效数字在某一数位,就说精确到某一数位.如:π=
3.141 592 6…, 若取3位有效数字,则x′=3.14,精确到0.01(即百分位);若取5位有效数字,则x′=3.141 6,精确到0.000 1(即万分位).课堂探究·素养提升题型一 二分法概念的理解[例1] (1)下列函数图象与x轴均有交点,其中不能用二分法求函数零点近似值的是( )解析:(1)能用二分法求函数零点的函数,在零点的左右两侧的函数值符号相反,图象要穿过x轴,B图象不穿过x轴.故选B.解析:(2)因为第一次所取的区间是[-2,4],所以第二次所取的区间可能是[-2,1],[1,4],第三次所取的区间可能为[-2,-0.5],[-0.5,1],[1, 2.5],[2.5,4],故选D.(2)在用二分法求函数f(x)零点近似值时,第一次取的区间是[-2,4],则第三次所取的区间可能是( )
(A)[1,4] (B)[-2,1]
(C)[-2,2.5] (D)[-0.5,1]方法技巧(1)用二分法求函数的零点近似值的方法仅对函数的变号零点适用,即条件f(a)·f(b)<0是必不可少的,对函数的不变号零点不适用.(2)使用二分法确定零点所在区间的原则是取与区间端点的值异号的区间中点.即时训练1-1:(1)(2019·湖南岳阳一中阶段检测)用二分法求如图所示的图象所表示的函数f(x)的零点时,不可能求出的零点是( )
(A)x1 (B)x2
(C)x3 (D)x4解析:(1)观察题中图象可知,x3附近两边的函数值都为负值,所以x3不能用二分法求得,故选C.答案:(1)C(2)某同学在借助计算器求“方程lg x=2-x的近似解(精确度0.1)”时,设f(x)=lg x+x-2,算得f(1)<0,f(2)>0.在以下过程中,使用“二分法”又取了4个x的值,计算了其函数值的正负,并得出判断:方程的近似解为x=1.8,那么他所取的x的4个值中最后一个值是 .答案:(2)1.812 5 [备用例1] (1)若函数f(x)=x2-4x+t存在零点,但不能用二分法求解,则t= .?
(2)已知函数f(x)=x3-2x-5,f(2.5)>0,用二分法求方程x3-2x-5=0在区间(2,3)内的实根,取区间中点为x0=2.5,那么下一个有根的区间是 .解析:(1)由题意知函数f(x)=x2-4x+t与x轴只有一个交点,
故Δ=16-4t=0,则t=4.
(2)因为f(2)=23-2×2-5=-1<0,
f(2.5)>0,f(3)=33-2×3-5=16>0,
所以f(2)·f(2.5)<0,
所以方程x3-2x-5=0在(2,2.5)内有实根.
答案:(1)4 (2)(2,2.5)题型二 二分法的步骤[例2] 用二分法求方程f(x)=0在[0,4]上的近似解时,最多经过 次计算精确度可以达到0.001. 答案:12方法技巧即时训练2-1:若用二分法求函数f(x)在(a,b)内的唯一零点时,精确度为0.001,则结束计算的条件是 .题型三 用二分法求方程的近似解[例3] 用二分法求方程x3-x-1=0在区间(1,1.5)内的一个近似解(精确度0.1).(提示:1.53=3.375,1.253≈1.953,1.3753≈2.6,1.312 53≈2.261)解:设f(x)=x3-x-1,
因为f(1)=1-1-1=-1<0,
f(1.5)=3.375-1.5-1=0.875>0,
所以f(x)在区间(1,1.5)上存在零点.
取区间(1,1.5)作为初始区间,用二分法逐次计算列表如下:因为|1.375-1.312 5|=0.062 5<0.1,
故函数f(x)=x3-x-1在(1,1.5)内的一个近似零点为1.375.
即方程x3-x-1=0在(1,1.5)内的一个近似解为1.375.方法技巧使用二分法求方程的近似解应转化为求其相应函数的近似零点,当区间两个端点在满足精确度条件下的近似值相等时,所得区间两个端点的近似值便为所求方程的根(或函数零点).即时训练3-1:利用二分法求方程ln x=3-x的根(精确度为0.1)(以下数据可供参考:ln 2.5≈0.916 3,ln 2.25≈0.810 9,ln 2.125≈0.753 8,
ln 2.75≈1.011 6,ln 2.187 5≈0.782 8,ln 2.218 75≈0.796 9,
ln 2.471 25≈0.904 7).解:令f(x)=ln x+x-3.
因为f(2)=ln 2-1<0,f(3)=ln 3>0,
所以取(2,3)作为函数零点计算的初始区间,用二分法逐次计算,列表如下:因为|2.187 5-2.25|=0.0625<0.1.
故函数f(x)=ln x+x-3在(2,3)内的一个近似零点为2.25.
所以方程ln x=3-x在(2,3)内的一个近似根为2.25.学霸经验分享区(1)使用“二分法”时应注意以下两点:
①选好计算的初始区间,保证所选区间既要符合条件,又要使其长度
最短;②计算时要根据给定的精确度,检验计算所得的区间是否满足这一
条件.1.用二分法求函数f(x)=2x-3的零点时,初始区间可选为( )
(A)(-1,0) (B)(0,1)
(C)(2,3) (D)(1,2)课堂达标D解析:由f(0)=1-3=-2,f(1)=-1,f(2)=1知选D.2.通过下列函数的图象,判断不能用“二分法”求其零点的是( )
(A)①②③ (B)②③④
(C)①②④ (D)①③④C解析:能用二分法求零点的函数必须在给定区间[a,b]上连续不断,并且有f(a)·f(b)<0,由图象可得,只有③能满足此条件,故不能用“二分法”求其零点的是①②④,故选C.D 4.用“二分法”可求近似解,对于精确度ε说法正确的是( )
(A)ε越大,零点的精确度越高
(B)ε越大,零点的精确度越低
(C)重复计算次数就是ε
(D)重复计算次数与ε无关B答案:f(x)=x5-2
