2019_2020学年高中数学第三章函数的应用3.2.1几类不同增长的函数模型课件新人教A版必修1:32张PPT
文档属性
| 名称 | 2019_2020学年高中数学第三章函数的应用3.2.1几类不同增长的函数模型课件新人教A版必修1:32张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 340.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 00:00:00 | ||
图片预览








文档简介
课件32张PPT。3.2 函数模型及其应用
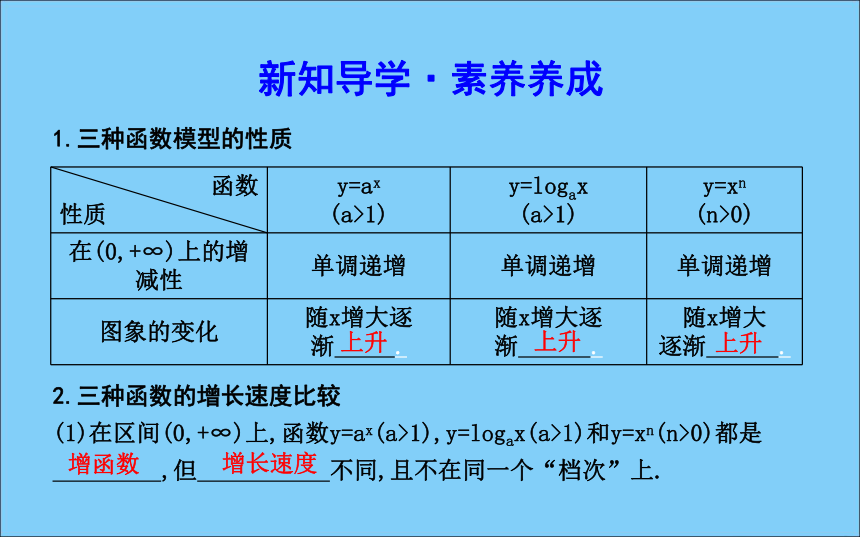
3.2.1 几类不同增长的函数模型[目标导航]新知导学·素养养成1.三种函数模型的性质上升上升上升2.三种函数的增长速度比较
(1)在区间(0,+∞)上,函数y=ax(a>1),y=logax(a>1)和y=xn(n>0)都是
,但 不同,且不在同一个“档次”上.增函数增长速度(2)随着x的增大,y=ax(a>1)增长速度越来越快,会超过并远远大于y=xn (n>0)的增长速度,而y=logax(a>1)的增长速度 .(3)存在一个x0,当x>x0时,有 .越来越慢logax(1)当a>1时,指数函数y=ax是增函数,且当a越大时,其函数值的增长就越快;(2)当a>1时,对数函数y=logax是增函数,且当a减小时,其函数值的增长就越快;
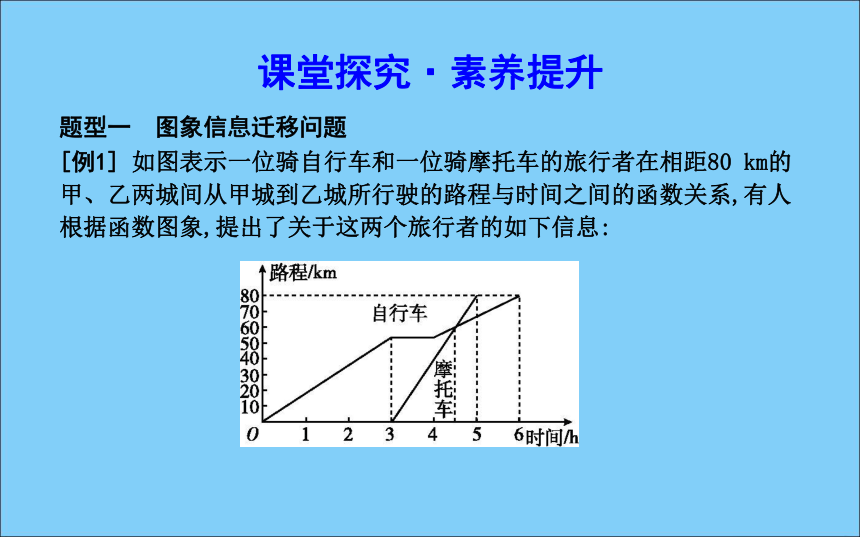
(3)当x>0,n>1时,幂函数y=xn是增函数,且当x>1时,n越大其函数值的增长就越快.课堂探究·素养提升题型一 图象信息迁移问题[例1] 如图表示一位骑自行车和一位骑摩托车的旅行者在相距80 km的甲、乙两城间从甲城到乙城所行驶的路程与时间之间的函数关系,有人根据函数图象,提出了关于这两个旅行者的如下信息:解析:看时间轴易知(1)正确;骑摩托车者行驶的路程与时间的函数图象是直线,所以是匀速运动,而骑自行车者行驶的路程与时间的函数图象是折线,所以是变速运动,因此(2)正确;两条曲线的交点的横坐标对应着4.5,故(3)正确,(4)错误.
答案:(1)(2)(3)(1)骑自行车者比骑摩托车者早出发3 h,晚到1 h;
(2)骑自行车者是变速运动,骑摩托车者是匀速运动;
(3)骑摩托车者在出发1.5 h后追上了骑自行车者;
(4)骑摩托车者在出发1.5 h后与骑自行车者速度一样.
其中正确信息的序号是 . 方法技巧解答图象信息迁移问题的技巧
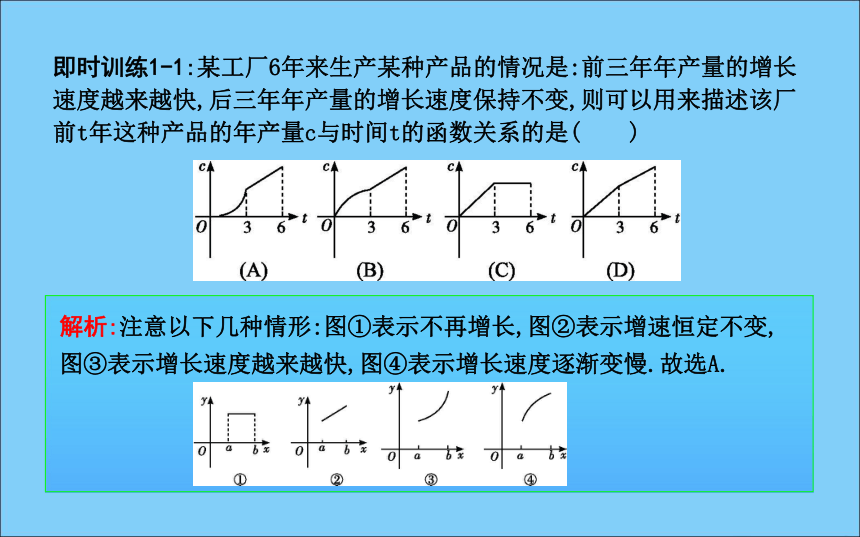
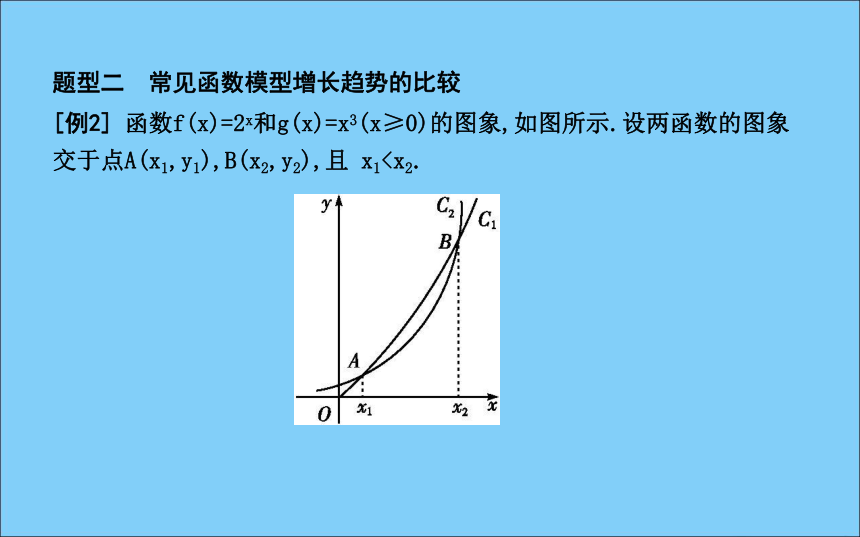
(1)明确横轴、纵轴的意义;(2)从图象形状上判定函数模型;(3)抓住特殊点的实际意义,特殊点一般包括最高点、最低点及折线的拐点等.即时训练1-1:某工厂6年来生产某种产品的情况是:前三年年产量的增长速度越来越快,后三年年产量的增长速度保持不变,则可以用来描述该厂前t年这种产品的年产量c与时间t的函数关系的是( )解析:注意以下几种情形:图①表示不再增长,图②表示增速恒定不变,图③表示增长速度越来越快,图④表示增长速度逐渐变慢.故选A.题型二 常见函数模型增长趋势的比较[例2] 函数f(x)=2x和g(x)=x3(x≥0)的图象,如图所示.设两函数的图象交于点A(x1,y1),B(x2,y2),且 x1(2)结合函数图象,比较f(8),g(8),f(2 015),g(2 015)的大小.解:(1)C1对应的函数为g(x)=x3(x≥0),C2对应的函数为f(x)=2x.
(2)因为g(1)=1,f(1)=2,g(2)=8,f(2)=4,g(9)=729,f(9)=512,g(10)=
1 000,f(10)=1 024,
所以f(1)>g(1),f(2)f(10)>g(10).
所以1所以x1<8从题中图象上知,当x1当x>x2时,f(x)>g(x),且g(x)在(0,+∞)上是增函数,
所以f(2 015)>g(2 015)>g(8)>f(8).方法技巧即时训练2-1:已知函数y1=2x,y2=x2,y3=log2x,则当 2(A)y1>y2>y3 (B)y2>y1>y3
(C)y1>y3>y2 (D)y2>y3>y1解析:法一 在同一平面直角坐标系中画出函数y3=log2x, y2=x2和y1=2x的图象,如图,在区间(2,4)内从上往下依次是y2=x2,y1=2x,y3=log2x的图象,所以对于任意x∈(2,4), x2>2x>log2x,即y2>y1>y3.故选B.法二 可以采用特殊值代入,如取x=3,则y1=8,y2=9,y3=log23<2,所以y2>y1>y3.故选B.[备用例1] 甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x-1,f2(x)=x2,f3(x)=x,f4(x)=log2(x+1),有以下结论:
①当x>0时,甲在最前面;
②当x>1时,乙在最前面;
③当01时,丁在最后面;
④丙不可能在最前面,也不可能在最后面;
⑤如果它们一直运动下去,那么最终在最前面的是甲.
其中,正确结论的序号为 (填序号).解析:路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系分别为f1(x)=2x-1,f2(x)=x2,f3(x)=x,f4(x)=log2(x+1),它们相应的函数模型分别是指数型函数、二次函数、一次函数和对数型函数.
当x=2时,f1(2)=3,f2(2)=4,所以①不正确.
当x=5时,f1(5)=31,f2(5)=25,所以②不正确.
根据四种函数的变化特点,对数型函数的增长速度是先快后慢,当x=1时,甲、乙、丙、丁四个物体的路程相等,从而可知当01时,丁在最后面,所以③正确.
指数函数的增长速度是先慢后快,当运动的时间足够长,最前面的物体一定是按照指数型函数运动的物体,即一定是甲,所以⑤正确.
结合对数型函数和指数函数的图象变化情况,可知丙不可能在最前面,也不可能在最后面,所以④正确.答案:③④⑤题型三 函数模型的选取[例3] 某工厂今年1月、2月、3月生产某种产品分别为1万件、1.2万件、1.3万件,为估测以后每个月的产量,以这三个月的产量为依据,用一个函数模拟该产品的月产量y和月份x的关系,模拟函数可以选用二次函数y= ax2+bx+c或函数y=a·bx+c(其中a,b,c为常数,a≠0,b>0且b≠1).已知4月份该产品的产量为1.37万件,问用上述哪一种函数作为模拟函数好?请说明理由.方法技巧开放型的探究题,函数模型不是确定的,需要我们去探索,去尝试,找到最合适的模型,解题过程一般为
(1)用待定系数法求出函数解析式;(2)检验:将(1)中求出的几个函数模型进行比较、验证,得出最适合的函数模型;
(3)利用所求出的函数模型解决问题.即时训练3-1:某工厂生产一种电脑元件,每月的生产数据如表:为估计以后每月对该电脑元件的产量,以这三个月的产量为依据,用函数y=ax+b或y=ax+b(a,b为常数,且a>0)来模拟这种电脑元件的月产量y千件与月份x的关系.请问:用以上哪个模拟函数较好?说明理由.(2)某新品牌电视投放市场后第一个月销售100台,第二个月销售200台,第三个月销售400台,第四个月销售790台,则下列函数模型中能较好反映销量y(台)与投放市场的月数x之间的关系是( )
(A)y=100x (B)y=50x2-50x+100
(C)y=50×2x (D)y=100log2x+100解析:(2)由题意,对于A中的函数,当x=3或4时,误差较大.对于B中的函数,当x=4时,误差也较大.对于C中的函数,当x=1,2,3时,误差为0,x=4时,误差为10,误差很小.对于D中的函数,当x=4时,y=300,与实际值790相差很大.综上,只有C中的函数误差最小,故选C.题型四 建立函数模型解决实际问题[例4] 一工厂生产某种零件,每个零件的成本为40元,出厂单价为60元,该厂为鼓励销售商订购,决定当一次订购量超过100时,每多订购1个,订购的全部零件的单价就降低 0.02元,但最低出厂单价不低于51元.
(1)一次订购量为多少个时,零件的实际出厂价恰好为51元? (2)设一次订购量为x个时零件的实际出厂价为p元,写出p=f(x)的关系式.(3)当销售商一次订购量分别为500,1 000个时,该工厂的利润分别为多少?(一个零件的利润=一个零件的实际出厂价-一个零件的成本)方法技巧数学建模中要对所给条件进行简化及合理的假设,从中区分出主要条件及次要条件,再根据要求选取合适的数学知识来求解.学霸经验分享区(1)不同的函数模型能刻画现实世界中不同的变化规律:
①线性函数增长模型适合于描述增长速度不变的变化规律;②指数函数增长模型适合于描述增长速度急剧的变化规律;
③对数函数增长模型适合于描述增长速度平缓的变化规律;
④幂函数增长模型适合于描述增长速度一般的变化规律.因此,需抓住题中蕴含的数学信息,恰当、准确地建立相应变化规律的函数模型来解决实际问题.
(2)若已知条件中给出一组数据选择数学模型时,可以在直角坐标系中将该组数据对应的点描出,根据点的分布特征选择数学模型.(3)一般来说,函数模型的增长速度与图象关系如下表:1.下列函数中,增长速度最快的是( )
(A)y=20x (B)y=x20
(C)y=log20x (D)y=20x课堂达标A2.对于两个变量x,y有如下几组数据:C解析:由于0.9接近20,4.1接近22,故该组数据满足y=2x.则x,y间拟合效果最好的曲线方程是( )
(A)y=log2x (B)y=2x
(C)y=2x (D)y=x23.某水果批发市场规定,批发某种水果不少于100 kg时,批发价为每千克2.5元,小王携现金3 000元到市场采购该种水果,并以批发价格买进,如果购买该种水果为x kg,小王付款后剩余现金为y元,则y与x之间的函数关系式为 .答案:y=3 000-2.5x,x∈[100,1 200]
3.2.1 几类不同增长的函数模型[目标导航]新知导学·素养养成1.三种函数模型的性质上升上升上升2.三种函数的增长速度比较
(1)在区间(0,+∞)上,函数y=ax(a>1),y=logax(a>1)和y=xn(n>0)都是
,但 不同,且不在同一个“档次”上.增函数增长速度(2)随着x的增大,y=ax(a>1)增长速度越来越快,会超过并远远大于y=xn (n>0)的增长速度,而y=logax(a>1)的增长速度 .(3)存在一个x0,当x>x0时,有 .越来越慢logax
(3)当x>0,n>1时,幂函数y=xn是增函数,且当x>1时,n越大其函数值的增长就越快.课堂探究·素养提升题型一 图象信息迁移问题[例1] 如图表示一位骑自行车和一位骑摩托车的旅行者在相距80 km的甲、乙两城间从甲城到乙城所行驶的路程与时间之间的函数关系,有人根据函数图象,提出了关于这两个旅行者的如下信息:解析:看时间轴易知(1)正确;骑摩托车者行驶的路程与时间的函数图象是直线,所以是匀速运动,而骑自行车者行驶的路程与时间的函数图象是折线,所以是变速运动,因此(2)正确;两条曲线的交点的横坐标对应着4.5,故(3)正确,(4)错误.
答案:(1)(2)(3)(1)骑自行车者比骑摩托车者早出发3 h,晚到1 h;
(2)骑自行车者是变速运动,骑摩托车者是匀速运动;
(3)骑摩托车者在出发1.5 h后追上了骑自行车者;
(4)骑摩托车者在出发1.5 h后与骑自行车者速度一样.
其中正确信息的序号是 . 方法技巧解答图象信息迁移问题的技巧
(1)明确横轴、纵轴的意义;(2)从图象形状上判定函数模型;(3)抓住特殊点的实际意义,特殊点一般包括最高点、最低点及折线的拐点等.即时训练1-1:某工厂6年来生产某种产品的情况是:前三年年产量的增长速度越来越快,后三年年产量的增长速度保持不变,则可以用来描述该厂前t年这种产品的年产量c与时间t的函数关系的是( )解析:注意以下几种情形:图①表示不再增长,图②表示增速恒定不变,图③表示增长速度越来越快,图④表示增长速度逐渐变慢.故选A.题型二 常见函数模型增长趋势的比较[例2] 函数f(x)=2x和g(x)=x3(x≥0)的图象,如图所示.设两函数的图象交于点A(x1,y1),B(x2,y2),且 x1
(2)因为g(1)=1,f(1)=2,g(2)=8,f(2)=4,g(9)=729,f(9)=512,g(10)=
1 000,f(10)=1 024,
所以f(1)>g(1),f(2)
所以1
所以f(2 015)>g(2 015)>g(8)>f(8).方法技巧即时训练2-1:已知函数y1=2x,y2=x2,y3=log2x,则当 2
(C)y1>y3>y2 (D)y2>y3>y1解析:法一 在同一平面直角坐标系中画出函数y3=log2x, y2=x2和y1=2x的图象,如图,在区间(2,4)内从上往下依次是y2=x2,y1=2x,y3=log2x的图象,所以对于任意x∈(2,4), x2>2x>log2x,即y2>y1>y3.故选B.法二 可以采用特殊值代入,如取x=3,则y1=8,y2=9,y3=log23<2,所以y2>y1>y3.故选B.[备用例1] 甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x-1,f2(x)=x2,f3(x)=x,f4(x)=log2(x+1),有以下结论:
①当x>0时,甲在最前面;
②当x>1时,乙在最前面;
③当0
④丙不可能在最前面,也不可能在最后面;
⑤如果它们一直运动下去,那么最终在最前面的是甲.
其中,正确结论的序号为 (填序号).解析:路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系分别为f1(x)=2x-1,f2(x)=x2,f3(x)=x,f4(x)=log2(x+1),它们相应的函数模型分别是指数型函数、二次函数、一次函数和对数型函数.
当x=2时,f1(2)=3,f2(2)=4,所以①不正确.
当x=5时,f1(5)=31,f2(5)=25,所以②不正确.
根据四种函数的变化特点,对数型函数的增长速度是先快后慢,当x=1时,甲、乙、丙、丁四个物体的路程相等,从而可知当0
指数函数的增长速度是先慢后快,当运动的时间足够长,最前面的物体一定是按照指数型函数运动的物体,即一定是甲,所以⑤正确.
结合对数型函数和指数函数的图象变化情况,可知丙不可能在最前面,也不可能在最后面,所以④正确.答案:③④⑤题型三 函数模型的选取[例3] 某工厂今年1月、2月、3月生产某种产品分别为1万件、1.2万件、1.3万件,为估测以后每个月的产量,以这三个月的产量为依据,用一个函数模拟该产品的月产量y和月份x的关系,模拟函数可以选用二次函数y= ax2+bx+c或函数y=a·bx+c(其中a,b,c为常数,a≠0,b>0且b≠1).已知4月份该产品的产量为1.37万件,问用上述哪一种函数作为模拟函数好?请说明理由.方法技巧开放型的探究题,函数模型不是确定的,需要我们去探索,去尝试,找到最合适的模型,解题过程一般为
(1)用待定系数法求出函数解析式;(2)检验:将(1)中求出的几个函数模型进行比较、验证,得出最适合的函数模型;
(3)利用所求出的函数模型解决问题.即时训练3-1:某工厂生产一种电脑元件,每月的生产数据如表:为估计以后每月对该电脑元件的产量,以这三个月的产量为依据,用函数y=ax+b或y=ax+b(a,b为常数,且a>0)来模拟这种电脑元件的月产量y千件与月份x的关系.请问:用以上哪个模拟函数较好?说明理由.(2)某新品牌电视投放市场后第一个月销售100台,第二个月销售200台,第三个月销售400台,第四个月销售790台,则下列函数模型中能较好反映销量y(台)与投放市场的月数x之间的关系是( )
(A)y=100x (B)y=50x2-50x+100
(C)y=50×2x (D)y=100log2x+100解析:(2)由题意,对于A中的函数,当x=3或4时,误差较大.对于B中的函数,当x=4时,误差也较大.对于C中的函数,当x=1,2,3时,误差为0,x=4时,误差为10,误差很小.对于D中的函数,当x=4时,y=300,与实际值790相差很大.综上,只有C中的函数误差最小,故选C.题型四 建立函数模型解决实际问题[例4] 一工厂生产某种零件,每个零件的成本为40元,出厂单价为60元,该厂为鼓励销售商订购,决定当一次订购量超过100时,每多订购1个,订购的全部零件的单价就降低 0.02元,但最低出厂单价不低于51元.
(1)一次订购量为多少个时,零件的实际出厂价恰好为51元? (2)设一次订购量为x个时零件的实际出厂价为p元,写出p=f(x)的关系式.(3)当销售商一次订购量分别为500,1 000个时,该工厂的利润分别为多少?(一个零件的利润=一个零件的实际出厂价-一个零件的成本)方法技巧数学建模中要对所给条件进行简化及合理的假设,从中区分出主要条件及次要条件,再根据要求选取合适的数学知识来求解.学霸经验分享区(1)不同的函数模型能刻画现实世界中不同的变化规律:
①线性函数增长模型适合于描述增长速度不变的变化规律;②指数函数增长模型适合于描述增长速度急剧的变化规律;
③对数函数增长模型适合于描述增长速度平缓的变化规律;
④幂函数增长模型适合于描述增长速度一般的变化规律.因此,需抓住题中蕴含的数学信息,恰当、准确地建立相应变化规律的函数模型来解决实际问题.
(2)若已知条件中给出一组数据选择数学模型时,可以在直角坐标系中将该组数据对应的点描出,根据点的分布特征选择数学模型.(3)一般来说,函数模型的增长速度与图象关系如下表:1.下列函数中,增长速度最快的是( )
(A)y=20x (B)y=x20
(C)y=log20x (D)y=20x课堂达标A2.对于两个变量x,y有如下几组数据:C解析:由于0.9接近20,4.1接近22,故该组数据满足y=2x.则x,y间拟合效果最好的曲线方程是( )
(A)y=log2x (B)y=2x
(C)y=2x (D)y=x23.某水果批发市场规定,批发某种水果不少于100 kg时,批发价为每千克2.5元,小王携现金3 000元到市场采购该种水果,并以批发价格买进,如果购买该种水果为x kg,小王付款后剩余现金为y元,则y与x之间的函数关系式为 .答案:y=3 000-2.5x,x∈[100,1 200]
