2019_2020学年高中数学第三章函数的应用3.2.2函数模型的应用实例课件新人教A版必修1:28张PPT
文档属性
| 名称 | 2019_2020学年高中数学第三章函数的应用3.2.2函数模型的应用实例课件新人教A版必修1:28张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 361.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 12:56:39 | ||
图片预览







文档简介
课件28张PPT。3.2.2 函数模型的应用实例[目标导航]新知导学·素养养成1.函数模型应用的两个方面
(1)利用已知函数模型解决问题.(2)建立恰当的函数模型,并利用所得函数模型解释有关现象,对某些发展趋势进行预测.
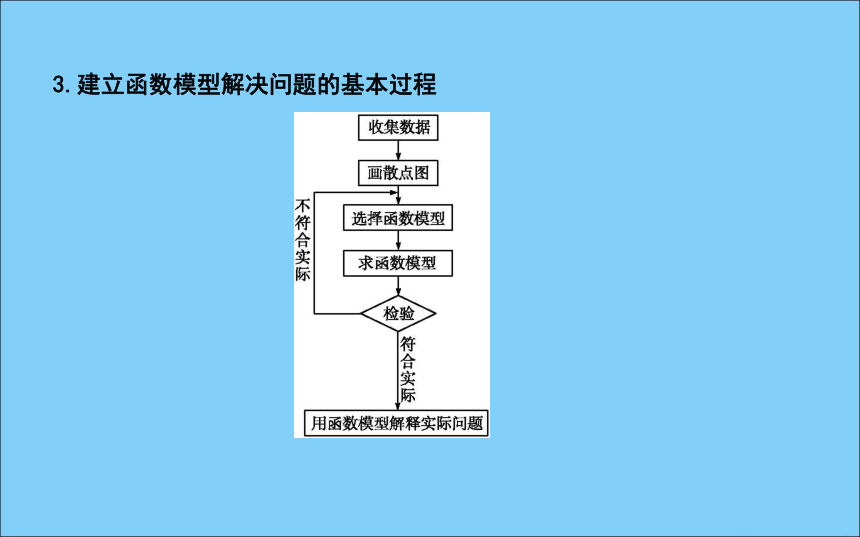
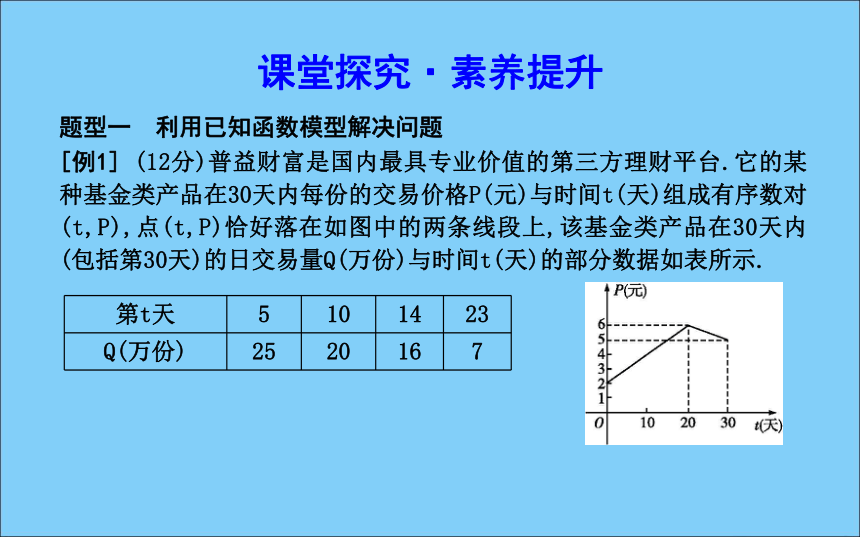
2.常见的函数模型ax+b(a,b为常数且a≠0)ax2+bx+c(a,b,c为常数且a≠0)k·ax+b(k,a,b为常数且a>0,a≠1,k≠0)k·xn+b(k,b,n为常数,且k≠0)3.建立函数模型解决问题的基本过程课堂探究·素养提升题型一 利用已知函数模型解决问题[例1] (12分)普益财富是国内最具专业价值的第三方理财平台.它的某种基金类产品在30天内每份的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)恰好落在如图中的两条线段上,该基金类产品在30天内(包括第30天)的日交易量Q(万份)与时间t(天)的部分数据如表所示.规范解答:(1)①由题图知该基金类产品每份交易价格P(元)与时间t(天)所满足的函数图象为两条线段,且在0~20天,图象经过点(0,2)和(20, 6),在20~30经过点(20,6)和(30,5),(1)①根据提供的图象,写出该基金类产品每份交易价格P(元)与时间t(天)所满足的函数关系式;
②根据表中数据确定日交易量Q(万份)与时间t(天)的一次函数关系式;
(2)在(1)的结论下,用y(万元)表示该基金类产品日交易额(日交易额=每份交易价格×日交易量),写出y关于t的函数关系式,并求出这30天中第几天的日交易额最大,最大值为多少?方法技巧利用已知函数模型求解实际问题时,要注意根据函数模型的特点寻找规律.涉及分段函数模型时,由于分段函数每一段自变量变化所遵循的规律不同,可以先将其当作几个问题,将各段的变化规律分别找出来,再将其合到一起,要注意各段变化量的范围,特别是端点值.即时训练1-1:据市场分析,烟台某海鲜加工公司,当月产量在10吨至25吨时,月生产总成本y(万元)可以看成月产量x(吨)的二次函数;当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元,为二次函数的顶点.
(1)写出月总成本y(万元)关于月产量x(吨)的函数关系;(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获得最大利润?题型二 指数型函数模型[例2] 诺贝尔奖发放方式为:每年一发,把奖金总额平均分成6份,奖励给分别在6项(物理、化学、文学、经济学、生理学和医学、和平)为人类作出最有益贡献的人,每年发放奖金的总金额是基金在该年度所获利息的一半,另一半利息作基金总额,以便保证奖金数逐年增加,假设基金平均年利率为r=6.24%,资料显示:2003年诺贝尔奖发放后基金总额约为
19 800万美元,设f(x)表示第x(x∈N*)年诺贝尔奖发放后的基金总额(2003年记为f(1),2004年记为f(2),…,依此类推).
(1)用f(1)表示f(2)和f(3),并根据所求结果归纳出函数f(x)的表达式;(2)试根据题中所给信息,判断2013年度的诺贝尔奖各项奖金为多少?(参考数据:1.031 29≈1.32)方法技巧题型三 对数型函数模型(2)若x0=5,候鸟停下休息时,它每分钟的耗氧量为多少个单位?(3)若雄鸟的飞行速度为2.5 km/min,雌鸟的飞行速度为1.5 km/min,那么此时雄鸟每分钟的耗氧量是雌鸟每分钟耗氧量的多少倍?方法技巧(1)形如y=mlogax+n(a>0,a≠1,m≠0),其特点为当a>1,m>0时,y随自变量x的增大而增大,且函数值增大的速度越来越慢.(2)对于对数型函数模型问题,关键在于熟练掌握对数函数的性质,在认真审题的基础上,分析清楚底数a与1的大小关系,要关注自变量的取值范围.
借助于数学模型解决数学问题的同时,实际问题也得以顺利解决,这就是函数模型的作用.即时训练3-1:某公司制定了一个激励销售人员的奖励方案:当销售利润不超过15万元时,按销售利润的10%进行奖励;当销售利润超过15万元时,若超过部分为A万元,则超出部分按2log5(A+1)进行奖励,没超出部分仍按销售利润的10%进行奖励.记奖金总额为y(单位:万元),销售利润为x(单位:万元).
(1)写出该公司激励销售人员的奖励方案的函数表达式;(2)如果业务员老张获得5.5万元的奖金,那么他的销售利润是多少万元?解:(2)由题意知老张的销售利润超过15万元,
故1.5+2log5(x-14)=5.5,所以x=39,
所以他的销售利润是39万元.题型四 易错辨析[例4] 生产一定数量的商品的全部费用称为生产成本,它可以表示为商品数量的函数.现知一企业生产某种商品的数量为x(件)时的成本函数为y=10+2x+2x2(万元),若售出一件商品的价格是20万元,那么该企业所能获取的最大利润是多少?错解:设该企业所能获取的利润为z万元,
则z=20x-(10+2x+2x2),
即z=-2x2+18x-10=-2(x-4.5)2+30.5,
故z的最大值为30.5,
即该企业所能获取的最大利润为30.5万元.纠错:(忽视自变量的实际意义)题目中的条件已经暗示了x为自然数,而错解中却是在x=4.5时取到的最大值30.5.正解:设该企业所能获取的利润为z万元,
则z=20x-(10+2x+2x2)(x∈N),
即z=-2x2+18x-10=-2(x-4.5)2+30.5,
故当x=4或5时,z取最大值30,
即该企业生产4件或5件商品时所取得的利润最大,为30万元.1.某林场计划第一年造林10 000亩,以后每年比前一年多造林20%,则第四年造林( )
(A)14 400亩 (B)172 800亩
(C)17 280亩 (D)20 736亩
2.某汽车运输公司购买了一批豪华大客车投入运营.据市场分析,每辆客车运营的利润y与运营年数x(x∈N)为二次函数关系(如图),则客车有运营利润的时间不超过( )
(A)4年 (B)5年
(C)6年 (D)7年课堂达标CD3.据调查,苹果园地铁的自行车存车处在某星期日的存车量为4 000辆次,其中变速车存车费是每辆一次0.3元,普通车存车费是每辆一次0.2元,若普通车存车数为x辆次,存车费总收入为y元,则y关于x的函数关系式是( )
(A)y=0.1x+800(0≤x≤4 000)
(B)y=0.1x+1 200(0≤x≤4 000)
(C)y=-0.1x+800(0≤x≤4 000)
(D)y=-0.1x+1 200(0≤x≤4 000)D
(1)利用已知函数模型解决问题.(2)建立恰当的函数模型,并利用所得函数模型解释有关现象,对某些发展趋势进行预测.
2.常见的函数模型ax+b(a,b为常数且a≠0)ax2+bx+c(a,b,c为常数且a≠0)k·ax+b(k,a,b为常数且a>0,a≠1,k≠0)k·xn+b(k,b,n为常数,且k≠0)3.建立函数模型解决问题的基本过程课堂探究·素养提升题型一 利用已知函数模型解决问题[例1] (12分)普益财富是国内最具专业价值的第三方理财平台.它的某种基金类产品在30天内每份的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)恰好落在如图中的两条线段上,该基金类产品在30天内(包括第30天)的日交易量Q(万份)与时间t(天)的部分数据如表所示.规范解答:(1)①由题图知该基金类产品每份交易价格P(元)与时间t(天)所满足的函数图象为两条线段,且在0~20天,图象经过点(0,2)和(20, 6),在20~30经过点(20,6)和(30,5),(1)①根据提供的图象,写出该基金类产品每份交易价格P(元)与时间t(天)所满足的函数关系式;
②根据表中数据确定日交易量Q(万份)与时间t(天)的一次函数关系式;
(2)在(1)的结论下,用y(万元)表示该基金类产品日交易额(日交易额=每份交易价格×日交易量),写出y关于t的函数关系式,并求出这30天中第几天的日交易额最大,最大值为多少?方法技巧利用已知函数模型求解实际问题时,要注意根据函数模型的特点寻找规律.涉及分段函数模型时,由于分段函数每一段自变量变化所遵循的规律不同,可以先将其当作几个问题,将各段的变化规律分别找出来,再将其合到一起,要注意各段变化量的范围,特别是端点值.即时训练1-1:据市场分析,烟台某海鲜加工公司,当月产量在10吨至25吨时,月生产总成本y(万元)可以看成月产量x(吨)的二次函数;当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元,为二次函数的顶点.
(1)写出月总成本y(万元)关于月产量x(吨)的函数关系;(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获得最大利润?题型二 指数型函数模型[例2] 诺贝尔奖发放方式为:每年一发,把奖金总额平均分成6份,奖励给分别在6项(物理、化学、文学、经济学、生理学和医学、和平)为人类作出最有益贡献的人,每年发放奖金的总金额是基金在该年度所获利息的一半,另一半利息作基金总额,以便保证奖金数逐年增加,假设基金平均年利率为r=6.24%,资料显示:2003年诺贝尔奖发放后基金总额约为
19 800万美元,设f(x)表示第x(x∈N*)年诺贝尔奖发放后的基金总额(2003年记为f(1),2004年记为f(2),…,依此类推).
(1)用f(1)表示f(2)和f(3),并根据所求结果归纳出函数f(x)的表达式;(2)试根据题中所给信息,判断2013年度的诺贝尔奖各项奖金为多少?(参考数据:1.031 29≈1.32)方法技巧题型三 对数型函数模型(2)若x0=5,候鸟停下休息时,它每分钟的耗氧量为多少个单位?(3)若雄鸟的飞行速度为2.5 km/min,雌鸟的飞行速度为1.5 km/min,那么此时雄鸟每分钟的耗氧量是雌鸟每分钟耗氧量的多少倍?方法技巧(1)形如y=mlogax+n(a>0,a≠1,m≠0),其特点为当a>1,m>0时,y随自变量x的增大而增大,且函数值增大的速度越来越慢.(2)对于对数型函数模型问题,关键在于熟练掌握对数函数的性质,在认真审题的基础上,分析清楚底数a与1的大小关系,要关注自变量的取值范围.
借助于数学模型解决数学问题的同时,实际问题也得以顺利解决,这就是函数模型的作用.即时训练3-1:某公司制定了一个激励销售人员的奖励方案:当销售利润不超过15万元时,按销售利润的10%进行奖励;当销售利润超过15万元时,若超过部分为A万元,则超出部分按2log5(A+1)进行奖励,没超出部分仍按销售利润的10%进行奖励.记奖金总额为y(单位:万元),销售利润为x(单位:万元).
(1)写出该公司激励销售人员的奖励方案的函数表达式;(2)如果业务员老张获得5.5万元的奖金,那么他的销售利润是多少万元?解:(2)由题意知老张的销售利润超过15万元,
故1.5+2log5(x-14)=5.5,所以x=39,
所以他的销售利润是39万元.题型四 易错辨析[例4] 生产一定数量的商品的全部费用称为生产成本,它可以表示为商品数量的函数.现知一企业生产某种商品的数量为x(件)时的成本函数为y=10+2x+2x2(万元),若售出一件商品的价格是20万元,那么该企业所能获取的最大利润是多少?错解:设该企业所能获取的利润为z万元,
则z=20x-(10+2x+2x2),
即z=-2x2+18x-10=-2(x-4.5)2+30.5,
故z的最大值为30.5,
即该企业所能获取的最大利润为30.5万元.纠错:(忽视自变量的实际意义)题目中的条件已经暗示了x为自然数,而错解中却是在x=4.5时取到的最大值30.5.正解:设该企业所能获取的利润为z万元,
则z=20x-(10+2x+2x2)(x∈N),
即z=-2x2+18x-10=-2(x-4.5)2+30.5,
故当x=4或5时,z取最大值30,
即该企业生产4件或5件商品时所取得的利润最大,为30万元.1.某林场计划第一年造林10 000亩,以后每年比前一年多造林20%,则第四年造林( )
(A)14 400亩 (B)172 800亩
(C)17 280亩 (D)20 736亩
2.某汽车运输公司购买了一批豪华大客车投入运营.据市场分析,每辆客车运营的利润y与运营年数x(x∈N)为二次函数关系(如图),则客车有运营利润的时间不超过( )
(A)4年 (B)5年
(C)6年 (D)7年课堂达标CD3.据调查,苹果园地铁的自行车存车处在某星期日的存车量为4 000辆次,其中变速车存车费是每辆一次0.3元,普通车存车费是每辆一次0.2元,若普通车存车数为x辆次,存车费总收入为y元,则y关于x的函数关系式是( )
(A)y=0.1x+800(0≤x≤4 000)
(B)y=0.1x+1 200(0≤x≤4 000)
(C)y=-0.1x+800(0≤x≤4 000)
(D)y=-0.1x+1 200(0≤x≤4 000)D
