2019_2020学年高中数学第三章函数的应用章末总结课件新人教A版必修1:26张PPT
文档属性
| 名称 | 2019_2020学年高中数学第三章函数的应用章末总结课件新人教A版必修1:26张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 532.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 12:50:56 | ||
图片预览







文档简介
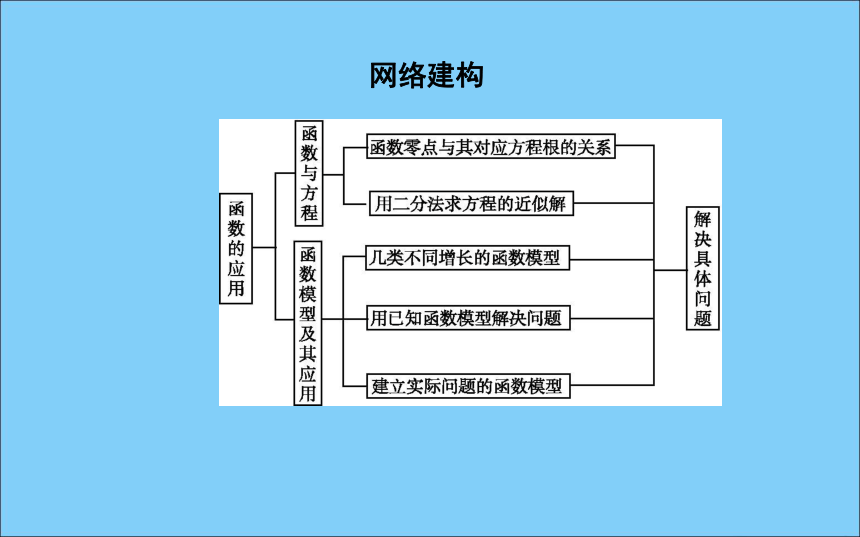
课件26张PPT。章末总结网络建构知识辨析判断下列说法是否正确(请在括号中填“√”或“×”)
1.函数的零点是一个点的坐标.( )×2.若函数y=f(x)在(a,b)内有零点,则f(a)·f(b)<0.( )
3.二次函数一定有零点.( )
4.若方程f(x)=0有两个不等实根x1,x2,则函数y=f(x)的零点为(x1,0), (x2,0).( )
5.所有函数的零点都可以用二分法来求.( )
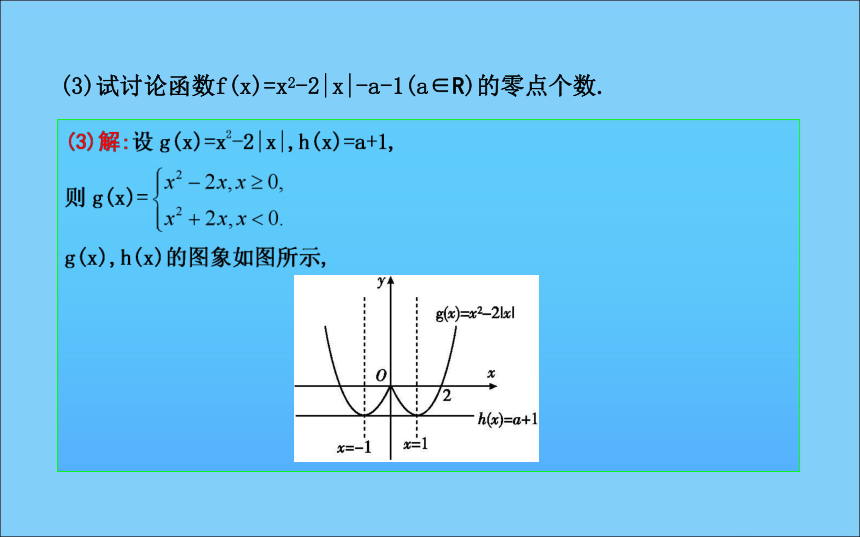
6.函数y=x2比y=2x增长的速度更快些.( )×××××√题型归纳·素养提升题型一 函数零点的判断(3)试讨论函数f(x)=x2-2|x|-a-1(a∈R)的零点个数.g(-2)=g(0)=g(2)=0,g(-1)=g(1)=-1,
当a+1<-1,即a<-2时,g(x)与h(x)无交点;
当a+1=-1或a+1>0,
即a=-2或a>-1时,g(x)与h(x)有两个交点;
当-1当a+1=0,即a=-1时,g(x)与h(x)有三个交点.
所以当a<-2时,函数f(x)=x2-2|x|-a-1无零点;
当a=-2或a>-1时,函数f(x)有两个零点;
当-2当a=-1时,函数f(x)有三个零点.规律方法(1)方程的根、函数的零点以及两函数图象交点的横坐标所在区间均可以转化为函数的零点,利用函数零点的存在性定理判断.(2)利用函数的单调性或数形结合思想判断函数零点个数. 题型二 函数零点的应用[典例2] (1)已知函数f(x)=|x(x+3)|,若h(x)=f(x)-x+b有四个零点,则实数b的取值范围是 .(1)解析:令f(x)-x+b=0,
所以b=x-|x(x+3)|,
作出y=x-|x(x+3)|的图象,
要使函数h(x)=f(x)-x+b有四个零点,
则y=x-|x(x+3)|与y=b的图象有四个不同的交点,所以-4旅游点规定:每辆自行车的日租金不低于3元并且不超过20元,每辆自行车的日租金x元只取整数,用y表示出租所有自行车的日净收入(即一日中出租的所有自行车的总收入减去管理费后的所得).
(1)求函数y=f(x)的解析式;(2)试问日净收入最多时每辆自行车的日租金应定为多少元?日净收入最多为多少元?规律方法(2)建模:将文字语言中含有相等意义的关键词转化成数学语言,即用等式表达,用数学知识建立相应的函数模型,即写出相关的函数解析式(注意有关量的实际意义,即函数的定义域).建立数学模型的步骤
(1)审题:弄清题意,分清条件和结论,理顺数量关系;真题体验·素养升级C解析:令h(x)=-x-a,
则g(x)=f(x)-h(x).
在同一坐标系中画出y=f(x),
y=h(x)图象的示意图,如图所示.
若g(x)存在2个零点,则y=f(x)的图象与y=h(x)的图象有2个交点,平移y=h(x)的图象,可知当直线y=-x-a过点(0,1)时,有2个交点,此时1=-0-a,a=-1.当y=-x-a在y=-x+1上方,即a<-1时,仅有1个交点,不符合题意.当y=-x-a在y=-x+1下方,即a>-1时,有2个交点,符合题意.综上,a的取值范围为[-1,+∞).故选C.答案:(1,4) (1,3]∪(4,+∞)解析:作出函数f(x)的示意图,如图,l1是过原点且与抛物线y=-x2+ 2ax-2a相切的直线,l2是过原点且与抛物线y=x2+2ax+a相切的直线.答案:(4,8)答案:244.(2015·四川卷)某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=ekx+b(e=2.718…为自然对数的底数,k,b为常数).若该食品在0 ℃的保鲜时间是192小时,在22 ℃的保鲜时间是48小时,则该食品在33 ℃的保鲜时间是 小时.
1.函数的零点是一个点的坐标.( )×2.若函数y=f(x)在(a,b)内有零点,则f(a)·f(b)<0.( )
3.二次函数一定有零点.( )
4.若方程f(x)=0有两个不等实根x1,x2,则函数y=f(x)的零点为(x1,0), (x2,0).( )
5.所有函数的零点都可以用二分法来求.( )
6.函数y=x2比y=2x增长的速度更快些.( )×××××√题型归纳·素养提升题型一 函数零点的判断(3)试讨论函数f(x)=x2-2|x|-a-1(a∈R)的零点个数.g(-2)=g(0)=g(2)=0,g(-1)=g(1)=-1,
当a+1<-1,即a<-2时,g(x)与h(x)无交点;
当a+1=-1或a+1>0,
即a=-2或a>-1时,g(x)与h(x)有两个交点;
当-1
所以当a<-2时,函数f(x)=x2-2|x|-a-1无零点;
当a=-2或a>-1时,函数f(x)有两个零点;
当-2
所以b=x-|x(x+3)|,
作出y=x-|x(x+3)|的图象,
要使函数h(x)=f(x)-x+b有四个零点,
则y=x-|x(x+3)|与y=b的图象有四个不同的交点,所以-4
(1)求函数y=f(x)的解析式;(2)试问日净收入最多时每辆自行车的日租金应定为多少元?日净收入最多为多少元?规律方法(2)建模:将文字语言中含有相等意义的关键词转化成数学语言,即用等式表达,用数学知识建立相应的函数模型,即写出相关的函数解析式(注意有关量的实际意义,即函数的定义域).建立数学模型的步骤
(1)审题:弄清题意,分清条件和结论,理顺数量关系;真题体验·素养升级C解析:令h(x)=-x-a,
则g(x)=f(x)-h(x).
在同一坐标系中画出y=f(x),
y=h(x)图象的示意图,如图所示.
若g(x)存在2个零点,则y=f(x)的图象与y=h(x)的图象有2个交点,平移y=h(x)的图象,可知当直线y=-x-a过点(0,1)时,有2个交点,此时1=-0-a,a=-1.当y=-x-a在y=-x+1上方,即a<-1时,仅有1个交点,不符合题意.当y=-x-a在y=-x+1下方,即a>-1时,有2个交点,符合题意.综上,a的取值范围为[-1,+∞).故选C.答案:(1,4) (1,3]∪(4,+∞)解析:作出函数f(x)的示意图,如图,l1是过原点且与抛物线y=-x2+ 2ax-2a相切的直线,l2是过原点且与抛物线y=x2+2ax+a相切的直线.答案:(4,8)答案:244.(2015·四川卷)某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=ekx+b(e=2.718…为自然对数的底数,k,b为常数).若该食品在0 ℃的保鲜时间是192小时,在22 ℃的保鲜时间是48小时,则该食品在33 ℃的保鲜时间是 小时.
