2019_2020学年高中数学第一章集合与函数概念1.1.3集合的基本运算第二课时补集及集合运算的综合应用课件新人教A:36张PPT版必修1
文档属性
| 名称 | 2019_2020学年高中数学第一章集合与函数概念1.1.3集合的基本运算第二课时补集及集合运算的综合应用课件新人教A:36张PPT版必修1 |  | |
| 格式 | zip | ||
| 文件大小 | 496.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 12:57:12 | ||
图片预览











文档简介
课件36张PPT。第二课时 补集及集合运算的综合应用[目标导航]新知导学·素养养成1.全集
一般地,如果一个集合含有我们所研究问题中涉及的 ,那么就称这个集合为全集.通常记作 .所有元素U2.补集不属于集合A?UA{x|x∈U,且x?A} 思考1:集合A与其补集能有公共元素吗?答案:由一个集合的补集的定义可知,集合A与其补集没有公共元素.思考2:如何理解全集与补集的关系?答案:(1)全集是涵盖了所有研究对象的一个集合,它因研究的问题而异,是一个相对概念;(2)研究补集时,一定要搞清楚是相对于哪个全集的补集,同一个集合相对于不同的全集,其补集是不同的;(3)?UA表示U为全集时A的补集,如果全部换成其他集合(如R)则?UA中U也必须换成相应的集合(如?RA);(4)?UA包括两个方面:首先A?U,即A是U的子集,其次是?UA=
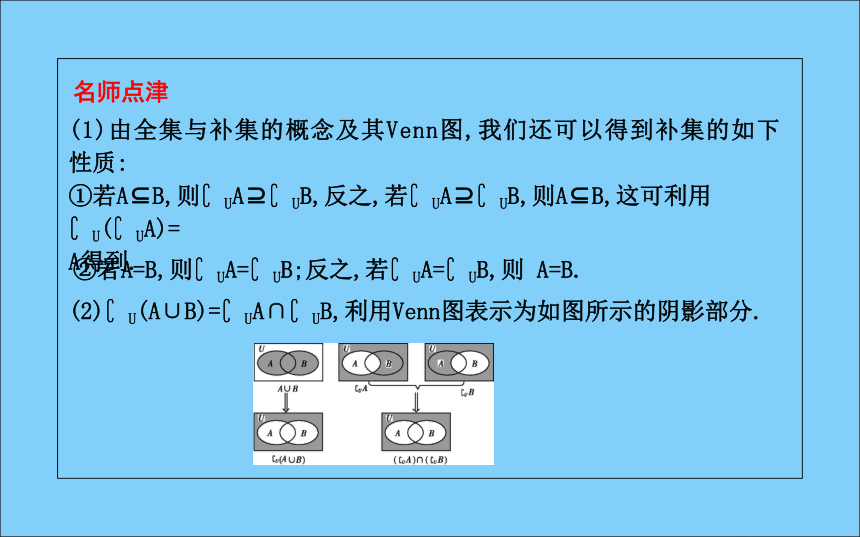
{x|x∈U,且x?A}.3.补集的运算性质名师点津(1)由全集与补集的概念及其Venn图,我们还可以得到补集的如下
性质:
①若A?B,则?UA??UB,反之,若?UA??UB,则A?B,这可利用?U(?UA)=
A得到.②若A=B,则?UA=?UB;反之,若?UA=?UB,则 A=B.(2)?U(A∪B)=?UA∩?UB,利用Venn图表示为如图所示的阴影部分.(3)?U(A∩B)=(?UA)∪(?UB),利用Venn图表示为如图所示的阴影部分.课堂探究·素养提升题型一 集合的补集运算[例1] (1)已知A={0,1,2},?UA={-3,-2,-1},?UB={-3,-2,0},用列举法写出集合B.解:(1)因为A={0,1,2},
?UA={-3,-2,-1},
所以U=A∪(?UA)={-3,-2,-1,0,1,2}.
又因为?UB={-3,-2,0},所以B={-1,1,2}.(2)若全集U={x|-3≤x≤3,x∈R},且集合A={x|-3≤x≤0或1求?UA.解:(2)由补集的定义可知?UA表示的集合为图中阴影部分所示,即?UA={x|0{-3,3,4},求?UA,?UB.解:法一 在集合U中,
因为x∈Z,则x的值为-5,-4,-3,3,4,5,
所以U={-5,-4,-3,3,4,5}.
又A={x|x2-2x-15=0}={-3,5},
B={-3,3,4},
所以?UA={-5,-4,3,4},
?UB={-5,-4,5}.法二 可用Venn图表示.
则?UA={-5,-4,3,4},?UB={-5,-4,5}.[备用例1] (1)设U={0,1,2,3},A={x|x2+mx=0}.若?UA={1,2},则实数m= .?解析:(1)因为U={0,1,2,3},?UA={1,2},所以A={0,3}.
又A={x|x2+mx=0},所以m=-3.答案:(1)-3 (2){a|a≥-5}(3)设全集I={2,3,x2+2x-3},A={5},?IA={2,y},求x,y的值.(3)解:因为A?I,所以5∈I,
所以x2+2x-3=5,即x2+2x-8=0,
解得x=-4或x=2.
因为y∈?IA,
所以y∈I,且y?A,即y≠5.
所以y=2或y=3.
又由?IA中元素的互异性知:y≠2,所以y=3.
综上知,x=-4或x=2,y=3.题型二 集合交集、并集、补集混合运算[例2] 已知集合S={x|1求:(1)(?SA)∩(?SB);(2)?S(A∪B);(3)(?SA)∪(?SB);(4)?S(A∩B).解:因为S={x|1x<2或5≤x≤7},?SB={x|1{x|2≤x<7},由此可得(1)(?SA)∩(?SB)={x|1(2)?S(A∪B)={x|1(3)(?SA)∪(?SB)={x|1(4)法一 A∩B={x|3≤x<5},所以?S(A∩B)={x|1法二 ?S(A∩B)={x|1(2)求解本题也可以直接利用补集的有关运算性质:?U(A∩B)=(?UA)∪
(?UB)与?U(A∪B)=(?UA)∩(?UB)求解.即时训练2-1:设全集U=R,集合A={x|-2B,?U(A∩B),(?UA)∩B.解:因为U=R,A={x|-2所以?UA={x|x≥3或x≤-2},A∩B={x|-2(?UA)∩B={x|x≥3或x≤-2}∩{x|-3={x|-3{x|x(A)a≥2 (B)a>2 (C)a≤1 (D)a<1(1)解析:因为A={x|xA∩(?UB)={4},U=R,求实数a,b的值.题型三 Venn图在集合运算中的应用[例3] 已知全集U={2,3,5,7,11,13,17,19}.若A∩(?UB)={3,5},(?UA)∩
B={7,19},(?UA)∩(?UB)={2,17},求集合A,B.解:由U={2,3,5,7,11,13,17,19},根据题设条件可画出如图所示的Venn图.
故A={3,5,11,13},B={7,11,13,19}.方法技巧(1)集合运算问题中若全集元素个数较少,且各元素之间是离散的,求已知条件中含全集子集的交、并、补集运算时,可借助Venn图求解.(2)使用Venn图解题时,对于全集U可被全集的两个子集A,B分成以下四部分,如图.
Ⅰ.A∩(?UB);Ⅱ.A∩B;Ⅲ.(?UA)∩B;
Ⅳ.?U(A∪B)(或(?UA)∩(?UB)).即时训练3-1:(2019·江西省南昌市八一中学、洪都中学高一联考)已知全集U=R,集合A={0,1,2,3,4},B={x|x>2或 x<0},则图中阴影部分表示的集合为( )
(A){0,1,2} (B){1,2}
(C){3,4} (D){0,3,4}解析:因为全集U=R,集合A={0,1,2,3,4},B={x|x>2或x<0},所以?UB={x|0≤x≤2},所以图中阴影部分表示的集合为A∩?UB={0,1,2},故选A.[备用例3] (1)对于全集U的子集M,N,若M是N的真子集,则下列集合中必为空集的是
(A)(?UM)∩N (B)M∩(?UN)
(C)(?UM)∩(?UN) (D)M∩N(2)如图,请用集合U,A,B,C分别表示下列部分所表示的集合:Ⅰ,Ⅱ,Ⅲ,
Ⅳ,Ⅴ,Ⅵ,Ⅶ,Ⅷ.(2)解:区域Ⅰ是三个集合的公共部分,因此I=A∩B∩C;区域Ⅱ是集合A与B的交集与集合C在U中的补集的交集,因此Ⅱ=(A∩B)∩(?UC);
区域Ⅲ是集合A与C的交集与集合B在U中的补集的交集,因此Ⅲ=(A∩
C)∩(?UB);
区域Ⅳ是集合B与C的交集与集合A在U中的补集的交集,因此Ⅳ=(B∩
C)∩?UA;
区域Ⅴ是集合A与集合B∪C在U中的补集的公共部分构成的,因此V=A∩
[?U(B∪C)];
同理可求Ⅵ=C∩[?U(A∪B)],Ⅶ=B∩[?U(A∪C)].
而区域Ⅷ是三个集合A,B,C在U中的补集,
因此Ⅷ=?U(A∪B∪C).题型四 补集思想的应用[例4] 已知集合A={x|0≤x≤2},B={x|a≤x≤a+3}.
(1)若(?RA)∪B≠R,求a的取值范围;(2)若A∩B≠A,求a的取值范围.一题多变:本题中已知条件不变,若(?RA)∩B≠B,求a的取值范围.解:因为A={x|0≤x≤2},
所以?RA={x|x<0或x>2}.
假设(?RA)∩B=B,则B?(?RA).
如图,则a+3<0或a>2,即a<-3或a>2.
所以当(?RA)∩B≠B时,
a的取值范围是{a|-3≤a≤2}.方法技巧求解数学问题时,若从问题的正面不易求解,可考虑问题的反面,这也就是“正难则反”的策略,这种“正难则反”的解题方法,运用的是补集思想,补集思想的一般思路是设全集为U,求其子集A,若直接求A较为困难,可先求?UA,再由?U(?UA)=A,求A.学霸经验分享区(1)涉及不等式解集的补集时,应先解不等式化简不等式后再求补集;
(2)求解与集合的补集有关的混和运算时,应先求补集后再进行集合的其他运算.课堂达标A1.设集合U=R,M={x|x>2或x<-2},则?UM等于( )
(A){x|-2≤x≤2} (B){x|-2(C){x|x<-2或x>2} (D){x|x≤-2或x≥2}解析:由M={x|x>2或x<-2}知?UM={x|-2≤x≤2}.选A.A解析:U=(?UM)∪M={0,2,4,6}.选A.D3.(2018·甘肃省张掖市高一上学期期末)设全集U={1,2,3,4,5},集合M={1,4},N={1,3,5},则N∩(?UM)等于( )
(A){1,3} (B){1,5} (C){4,5} (D){3,5}解析:全集U={1,2,3,4,5},
集合M={1,4},?UM={2,3,5},N={1,3,5},
所以N∩(?UM)={3,5}.
故选D.D4.已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则(?UA)∪B为
( )
(A){1,2,4} (B){2,3,4}
(C){0,2,3,4} (D){0,2,4}解析:因为?UA={0,4},所以(?UA)∪B={0,2,4}.故选D.5.已知全集U={1,2,3},集合A={1,m},?UA={2},则实数m= .?解析:因为A={1,m},?UA={2}且全集U={1,2,3}.
所以m=3.答案:3
一般地,如果一个集合含有我们所研究问题中涉及的 ,那么就称这个集合为全集.通常记作 .所有元素U2.补集不属于集合A?UA{x|x∈U,且x?A} 思考1:集合A与其补集能有公共元素吗?答案:由一个集合的补集的定义可知,集合A与其补集没有公共元素.思考2:如何理解全集与补集的关系?答案:(1)全集是涵盖了所有研究对象的一个集合,它因研究的问题而异,是一个相对概念;(2)研究补集时,一定要搞清楚是相对于哪个全集的补集,同一个集合相对于不同的全集,其补集是不同的;(3)?UA表示U为全集时A的补集,如果全部换成其他集合(如R)则?UA中U也必须换成相应的集合(如?RA);(4)?UA包括两个方面:首先A?U,即A是U的子集,其次是?UA=
{x|x∈U,且x?A}.3.补集的运算性质名师点津(1)由全集与补集的概念及其Venn图,我们还可以得到补集的如下
性质:
①若A?B,则?UA??UB,反之,若?UA??UB,则A?B,这可利用?U(?UA)=
A得到.②若A=B,则?UA=?UB;反之,若?UA=?UB,则 A=B.(2)?U(A∪B)=?UA∩?UB,利用Venn图表示为如图所示的阴影部分.(3)?U(A∩B)=(?UA)∪(?UB),利用Venn图表示为如图所示的阴影部分.课堂探究·素养提升题型一 集合的补集运算[例1] (1)已知A={0,1,2},?UA={-3,-2,-1},?UB={-3,-2,0},用列举法写出集合B.解:(1)因为A={0,1,2},
?UA={-3,-2,-1},
所以U=A∪(?UA)={-3,-2,-1,0,1,2}.
又因为?UB={-3,-2,0},所以B={-1,1,2}.(2)若全集U={x|-3≤x≤3,x∈R},且集合A={x|-3≤x≤0或1
因为x∈Z,则x的值为-5,-4,-3,3,4,5,
所以U={-5,-4,-3,3,4,5}.
又A={x|x2-2x-15=0}={-3,5},
B={-3,3,4},
所以?UA={-5,-4,3,4},
?UB={-5,-4,5}.法二 可用Venn图表示.
则?UA={-5,-4,3,4},?UB={-5,-4,5}.[备用例1] (1)设U={0,1,2,3},A={x|x2+mx=0}.若?UA={1,2},则实数m= .?解析:(1)因为U={0,1,2,3},?UA={1,2},所以A={0,3}.
又A={x|x2+mx=0},所以m=-3.答案:(1)-3 (2){a|a≥-5}(3)设全集I={2,3,x2+2x-3},A={5},?IA={2,y},求x,y的值.(3)解:因为A?I,所以5∈I,
所以x2+2x-3=5,即x2+2x-8=0,
解得x=-4或x=2.
因为y∈?IA,
所以y∈I,且y?A,即y≠5.
所以y=2或y=3.
又由?IA中元素的互异性知:y≠2,所以y=3.
综上知,x=-4或x=2,y=3.题型二 集合交集、并集、补集混合运算[例2] 已知集合S={x|1
(?UB)与?U(A∪B)=(?UA)∩(?UB)求解.即时训练2-1:设全集U=R,集合A={x|-2
B={7,19},(?UA)∩(?UB)={2,17},求集合A,B.解:由U={2,3,5,7,11,13,17,19},根据题设条件可画出如图所示的Venn图.
故A={3,5,11,13},B={7,11,13,19}.方法技巧(1)集合运算问题中若全集元素个数较少,且各元素之间是离散的,求已知条件中含全集子集的交、并、补集运算时,可借助Venn图求解.(2)使用Venn图解题时,对于全集U可被全集的两个子集A,B分成以下四部分,如图.
Ⅰ.A∩(?UB);Ⅱ.A∩B;Ⅲ.(?UA)∩B;
Ⅳ.?U(A∪B)(或(?UA)∩(?UB)).即时训练3-1:(2019·江西省南昌市八一中学、洪都中学高一联考)已知全集U=R,集合A={0,1,2,3,4},B={x|x>2或 x<0},则图中阴影部分表示的集合为( )
(A){0,1,2} (B){1,2}
(C){3,4} (D){0,3,4}解析:因为全集U=R,集合A={0,1,2,3,4},B={x|x>2或x<0},所以?UB={x|0≤x≤2},所以图中阴影部分表示的集合为A∩?UB={0,1,2},故选A.[备用例3] (1)对于全集U的子集M,N,若M是N的真子集,则下列集合中必为空集的是
(A)(?UM)∩N (B)M∩(?UN)
(C)(?UM)∩(?UN) (D)M∩N(2)如图,请用集合U,A,B,C分别表示下列部分所表示的集合:Ⅰ,Ⅱ,Ⅲ,
Ⅳ,Ⅴ,Ⅵ,Ⅶ,Ⅷ.(2)解:区域Ⅰ是三个集合的公共部分,因此I=A∩B∩C;区域Ⅱ是集合A与B的交集与集合C在U中的补集的交集,因此Ⅱ=(A∩B)∩(?UC);
区域Ⅲ是集合A与C的交集与集合B在U中的补集的交集,因此Ⅲ=(A∩
C)∩(?UB);
区域Ⅳ是集合B与C的交集与集合A在U中的补集的交集,因此Ⅳ=(B∩
C)∩?UA;
区域Ⅴ是集合A与集合B∪C在U中的补集的公共部分构成的,因此V=A∩
[?U(B∪C)];
同理可求Ⅵ=C∩[?U(A∪B)],Ⅶ=B∩[?U(A∪C)].
而区域Ⅷ是三个集合A,B,C在U中的补集,
因此Ⅷ=?U(A∪B∪C).题型四 补集思想的应用[例4] 已知集合A={x|0≤x≤2},B={x|a≤x≤a+3}.
(1)若(?RA)∪B≠R,求a的取值范围;(2)若A∩B≠A,求a的取值范围.一题多变:本题中已知条件不变,若(?RA)∩B≠B,求a的取值范围.解:因为A={x|0≤x≤2},
所以?RA={x|x<0或x>2}.
假设(?RA)∩B=B,则B?(?RA).
如图,则a+3<0或a>2,即a<-3或a>2.
所以当(?RA)∩B≠B时,
a的取值范围是{a|-3≤a≤2}.方法技巧求解数学问题时,若从问题的正面不易求解,可考虑问题的反面,这也就是“正难则反”的策略,这种“正难则反”的解题方法,运用的是补集思想,补集思想的一般思路是设全集为U,求其子集A,若直接求A较为困难,可先求?UA,再由?U(?UA)=A,求A.学霸经验分享区(1)涉及不等式解集的补集时,应先解不等式化简不等式后再求补集;
(2)求解与集合的补集有关的混和运算时,应先求补集后再进行集合的其他运算.课堂达标A1.设集合U=R,M={x|x>2或x<-2},则?UM等于( )
(A){x|-2≤x≤2} (B){x|-2
(A){1,3} (B){1,5} (C){4,5} (D){3,5}解析:全集U={1,2,3,4,5},
集合M={1,4},?UM={2,3,5},N={1,3,5},
所以N∩(?UM)={3,5}.
故选D.D4.已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则(?UA)∪B为
( )
(A){1,2,4} (B){2,3,4}
(C){0,2,3,4} (D){0,2,4}解析:因为?UA={0,4},所以(?UA)∪B={0,2,4}.故选D.5.已知全集U={1,2,3},集合A={1,m},?UA={2},则实数m= .?解析:因为A={1,m},?UA={2}且全集U={1,2,3}.
所以m=3.答案:3
