2019_2020学年高中数学第一章集合与函数概念1.2.1函数的概念第二课时函数概念的应用课件新人教A版必修1:34张PPT
文档属性
| 名称 | 2019_2020学年高中数学第一章集合与函数概念1.2.1函数的概念第二课时函数概念的应用课件新人教A版必修1:34张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 610.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 12:49:27 | ||
图片预览










文档简介
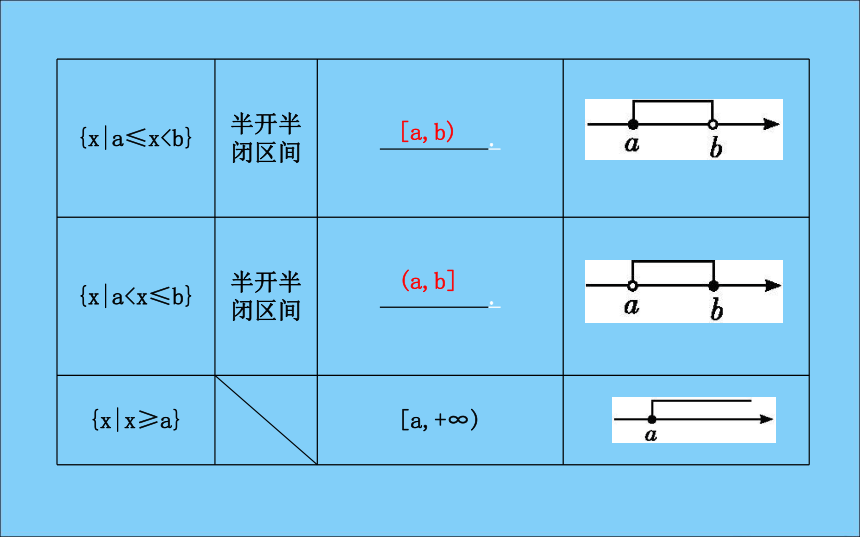
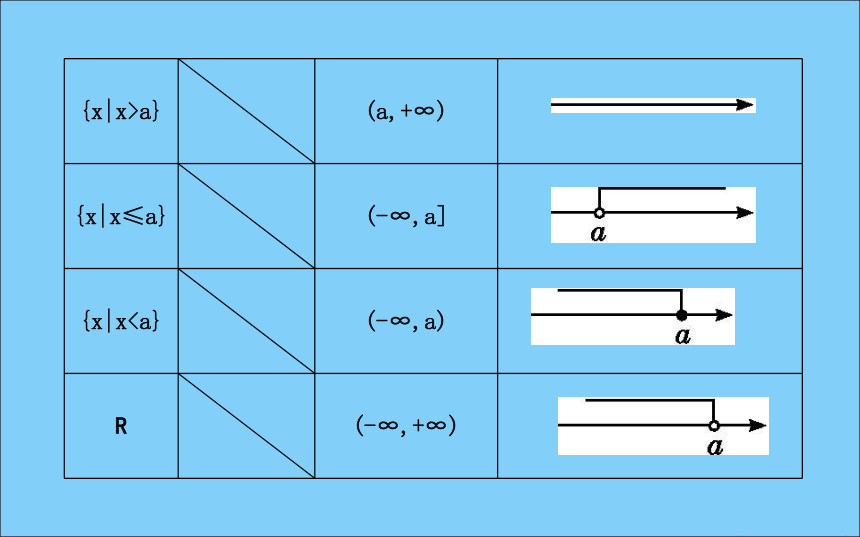
课件34张PPT。第二课时 函数概念的应用[目标导航]新知导学·素养养成1.区间
设a,b∈R,且a 、对应关系、值域.定义域3.相等函数
如果两个函数的 相同,并且 完全一致,我们就称这两个函数相等.定义域对应关系思考3:函数f(x)=x2,x∈R与g(t)=t2,t∈R是不是相等函数?答案:两个函数都是描述的同一集合R中任一元素,按同一对应关系“平方”对应B中唯一确定的元素,故是相等函数,由此可以看出,两个函数是否为相等函数,与函数用什么样的字母表示无关.方法技巧(1)区间概念的理解.
①区间实际上是一类特殊的数集(连续的)的符号表示,是集合的另一种表达方式,开或闭不能混淆.
②若[a,b]是确定区间,则必有a③区间符号里面的两个字母(或数字)之间要用“,”隔开.
④区间的几何表示:在数轴上表示区间时,用实心点表示在区间内的端点,用空心圈表示不包括在区间内的端点.
⑤由于区间是表示数集的一种形式,因此对于集合的运算仍然成立.
(2)常见函数的值域.
①一次函数y=kx+b(k≠0)的值域、定义域均为R.课堂探究·素养提升题型一 区间的表示[例1] 把下列数集用区间表示:
(1){x|x≥-1};(2){x|x<0};(3){x|-1(2){x|x<0}用区间表示为(-∞,0).
(3){x|-1(4){x|0①区间左端点值小于右端点值;
②区间两端点之间用“,”隔开;
③含端点值的一端用中括号,不含端点值的一端用小括号;
④以“-∞”,“+∞”为区间的一端时,这端必须用小括号.即时训练1-1:(1)用区间表示{x|x≥0且x≠2}为 ;?
(2)已知区间[a,2a+1],则a的取值范围是 .?解析:(1)[0,2)∪(2,+∞).
(2)因为2a+1>a,所以a>-1,即a∈(-1,+∞).答案:(1) [0,2)∪(2,+∞)
(2)(-1,+∞)题型二 相等函数的判定[例2] (2019·四川省蓉城名校联盟高一上学期期中联考)下列各组函数中,表示同一组函数的是( )方法技巧判断两个函数相等的方法
判断两个函数是否相等,要先求定义域,若定义域不同,则不相等;若定义域相同,再化简函数的解析式,若解析式相同,则相等,否则不
相等.题型三 求函数值域一题多变2:将本题(2)变为:①y=x2+2x(x∈R);②y=x2+2x(x∈[0,+∞));③y=x2+2x(x∈[-3,0)).分别求值域.解:因为y=x2+2x=(x+1)2-1.
当x∈R时,y≥-1.
故①中函数值域为[-1,+∞).
当x∈[0,+∞)时,
如图(1)可知函数值域为[0,+∞).
当x∈[-3,0)时,
如图(2)可知函数值域为[-1,3].方法技巧(2)逐值求解法:当函数定义域为有限元素构成的集合时,常用此法;
(3)配方法:若函数是二次函数形式,即可化为y=ax2+bx+c(a≠0)型的函数,则可通过配方后结合二次函数的性质求值域,当函数为二次函数且定义域为给定的区间(非全体实数)时,还要利用二次函数图象求解.(3)y=-x2+2x+1=-(x-1)2+2.如图为y=-x2+2x+1在x∈[0,3]时的大致图象,由图象可知函数值域为[-2,2].题型四 易错辨析[例4] 已知集合A=(2m-1,m+1),集合B=(-3,5),若A?B,则实数m的取值范围是 .?答案:[-1,+∞)答案:[-1,2)课堂达标C1.(2019·辽宁省葫芦岛协作校高一上学期第一次联考)函数f(x)=3x+2,
x∈[0,1]的值域为( )
(A)R (B)[0,1]
(C)[2,5] (D)[5,+∞)解析:因为x∈[0,1],所以0≤3x≤3.所以2≤3x+2≤5.选C.C解析:函数f(x)的定义域为[0,+∞),即D=[0,+∞).故选C.CB4.已知函数y=f(x)的定义域为A,值域为B,则关于函数y=2+f(x)的定义域、值域情况下列说法正确的是( )
(A)值域不变,定义域改变
(B)定义域不变,值域改变
(C)定义域、值域均不变
(D)定义域、值域均改变解析:由于函数y=f(x)与y=2+f(x)定义域相同,因此定义域不变,值域改变.故选B.5.集合{x|x∈R,x≠-1且x≠2}用区间表示为 .?答案:(-∞,-1)∪(-1,2)∪(2,+∞)
设a,b∈R,且a
如果两个函数的 相同,并且 完全一致,我们就称这两个函数相等.定义域对应关系思考3:函数f(x)=x2,x∈R与g(t)=t2,t∈R是不是相等函数?答案:两个函数都是描述的同一集合R中任一元素,按同一对应关系“平方”对应B中唯一确定的元素,故是相等函数,由此可以看出,两个函数是否为相等函数,与函数用什么样的字母表示无关.方法技巧(1)区间概念的理解.
①区间实际上是一类特殊的数集(连续的)的符号表示,是集合的另一种表达方式,开或闭不能混淆.
②若[a,b]是确定区间,则必有a
④区间的几何表示:在数轴上表示区间时,用实心点表示在区间内的端点,用空心圈表示不包括在区间内的端点.
⑤由于区间是表示数集的一种形式,因此对于集合的运算仍然成立.
(2)常见函数的值域.
①一次函数y=kx+b(k≠0)的值域、定义域均为R.课堂探究·素养提升题型一 区间的表示[例1] 把下列数集用区间表示:
(1){x|x≥-1};(2){x|x<0};(3){x|-1
(3){x|-1
②区间两端点之间用“,”隔开;
③含端点值的一端用中括号,不含端点值的一端用小括号;
④以“-∞”,“+∞”为区间的一端时,这端必须用小括号.即时训练1-1:(1)用区间表示{x|x≥0且x≠2}为 ;?
(2)已知区间[a,2a+1],则a的取值范围是 .?解析:(1)[0,2)∪(2,+∞).
(2)因为2a+1>a,所以a>-1,即a∈(-1,+∞).答案:(1) [0,2)∪(2,+∞)
(2)(-1,+∞)题型二 相等函数的判定[例2] (2019·四川省蓉城名校联盟高一上学期期中联考)下列各组函数中,表示同一组函数的是( )方法技巧判断两个函数相等的方法
判断两个函数是否相等,要先求定义域,若定义域不同,则不相等;若定义域相同,再化简函数的解析式,若解析式相同,则相等,否则不
相等.题型三 求函数值域一题多变2:将本题(2)变为:①y=x2+2x(x∈R);②y=x2+2x(x∈[0,+∞));③y=x2+2x(x∈[-3,0)).分别求值域.解:因为y=x2+2x=(x+1)2-1.
当x∈R时,y≥-1.
故①中函数值域为[-1,+∞).
当x∈[0,+∞)时,
如图(1)可知函数值域为[0,+∞).
当x∈[-3,0)时,
如图(2)可知函数值域为[-1,3].方法技巧(2)逐值求解法:当函数定义域为有限元素构成的集合时,常用此法;
(3)配方法:若函数是二次函数形式,即可化为y=ax2+bx+c(a≠0)型的函数,则可通过配方后结合二次函数的性质求值域,当函数为二次函数且定义域为给定的区间(非全体实数)时,还要利用二次函数图象求解.(3)y=-x2+2x+1=-(x-1)2+2.如图为y=-x2+2x+1在x∈[0,3]时的大致图象,由图象可知函数值域为[-2,2].题型四 易错辨析[例4] 已知集合A=(2m-1,m+1),集合B=(-3,5),若A?B,则实数m的取值范围是 .?答案:[-1,+∞)答案:[-1,2)课堂达标C1.(2019·辽宁省葫芦岛协作校高一上学期第一次联考)函数f(x)=3x+2,
x∈[0,1]的值域为( )
(A)R (B)[0,1]
(C)[2,5] (D)[5,+∞)解析:因为x∈[0,1],所以0≤3x≤3.所以2≤3x+2≤5.选C.C解析:函数f(x)的定义域为[0,+∞),即D=[0,+∞).故选C.CB4.已知函数y=f(x)的定义域为A,值域为B,则关于函数y=2+f(x)的定义域、值域情况下列说法正确的是( )
(A)值域不变,定义域改变
(B)定义域不变,值域改变
(C)定义域、值域均不变
(D)定义域、值域均改变解析:由于函数y=f(x)与y=2+f(x)定义域相同,因此定义域不变,值域改变.故选B.5.集合{x|x∈R,x≠-1且x≠2}用区间表示为 .?答案:(-∞,-1)∪(-1,2)∪(2,+∞)
