2019_2020学年高中数学第一章集合与函数概念1.2.2函数的表示法第一课时函数的表示法课件新人教A版必修1:38张PPT
文档属性
| 名称 | 2019_2020学年高中数学第一章集合与函数概念1.2.2函数的表示法第一课时函数的表示法课件新人教A版必修1:38张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 649.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 00:00:00 | ||
图片预览









文档简介
课件38张PPT。1.2.2 函数的表示法
第一课时 函数的表示法[目标导航]新知导学·素养养成1.函数的表示方法
解析法,就是用 表示两个变量之间的对应关系.
图象法,就是用 表示两个变量之间的对应关系.
列表法,就是 来表示两个变量之间的对应关系.数学表达式图象列出表格思考1:任何一个函数都可以用解析法表示吗?
答案:不是,并不是所有的函数都可以用解析法表示,如某地区一天中每时每刻的温度,由于受自然影响较大,无法用函数解析式表示.
思考2:函数f(x)=1中无自变量是一个函数解析式吗?
答案:是.该函数的函数值不因自变量的变化而变化,是一个常值函数.2.函数的图象
函数图象既可以是连续的曲线,也可以是直线、折线、离散点等.思考3:函数y=f(x)的图象的集合表示形式是什么?
答案:若y=f(x)的定义域为A,则y=f(x)图象的集合表示形式是{(x,y)|
y=f(x),x∈A}.名师点津(1)对画函数图象三个步骤的认识
①列表:先找出一些有代表性的自变量x的值,并计算出与这些自变量相对应的函数值f(x),用表格的形式表示出来.②描点:把第①步表格中的点(x,f(x))一一在坐标平面上描出来.
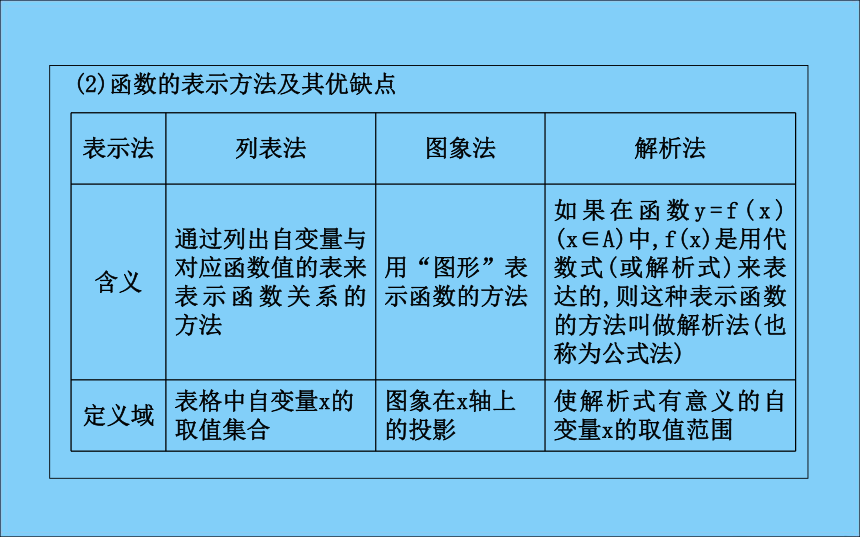
③连线:用平滑的曲线把这些点按自变量由小到大的顺序连接起来.(2)函数的表示方法及其优缺点(3)常用的图象变换
①平移变换
a.把函数y=f(x)的图象沿x轴向左(a>0)或向右(a<0)平移|a|个单位长度,就得到函数y=f(x+a)的图象;
b.把函数y=f(x)的图象沿y轴向上(a>0)或向下(a<0)平移|a|个单位长度,就得到函数y=f(x)+a的图象.简记为“上加下减,左加右减”.②对称翻折变换
a.形如y=f(-x)的函数,其函数图象与函数y=f(x)的图象关于y轴对称;
b.形如y=-f(x)的函数,其函数图象与函数y=f(x)的图象关于x轴对称;c.形如y=-f(-x)的函数,其函数图象与函数y=f(x) 的图象关于原点对称;
d.形如y=|f(x)|的函数,将函数y=f(x)的图象在x轴下方的部分沿x轴翻转到x轴上方(下方部分不再保留),x轴上方的图象不变,从而得到函数y=|f(x)|的图象;
e.形如y=f(|x|)的函数,可先作x>0时f(x)的图象,然后将函数y=f(x)的图象y轴右边的部分翻折到y轴左边,y轴右边的图象不变,从而得到函数y=f(|x|)的图象.课堂探究·素养提升题型一 函数图象的作法及应用
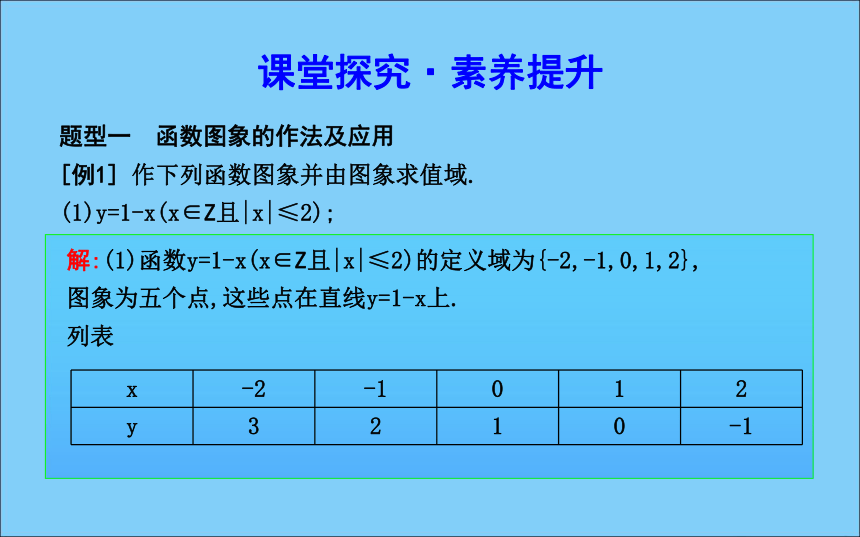
[例1] 作下列函数图象并由图象求值域.
(1)y=1-x(x∈Z且|x|≤2);解:(1)函数y=1-x(x∈Z且|x|≤2)的定义域为{-2,-1,0,1,2},
图象为五个点,这些点在直线y=1-x上.
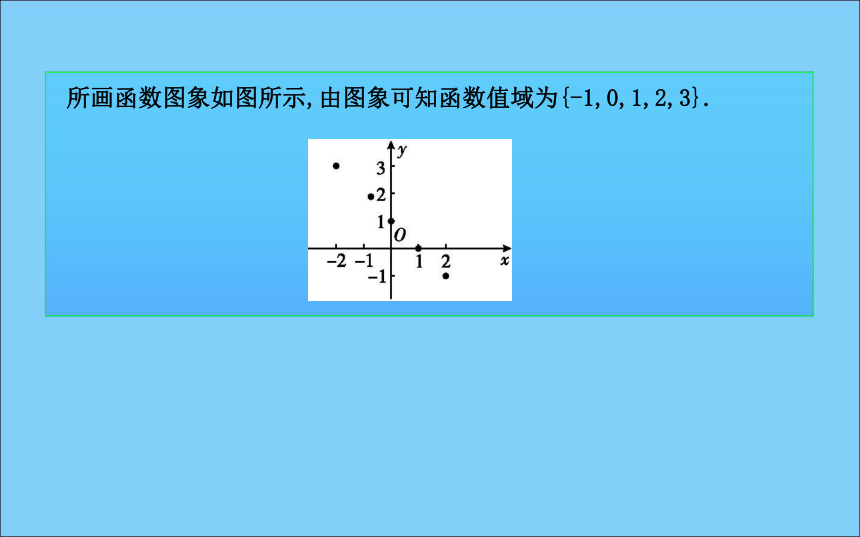
列表所画函数图象如图所示,由图象可知函数值域为{-1,0,1,2,3}.(2)y=x2-2x-3(x∈R);解:(2)函数y=x2-2x-3=(x-1)2-4,
列表所画函数图象如图所示,由图象可知函数值域为{y|y≥-4}.一题多变1:本题(2)中,将x∈R改为x∈[-2,3],则函数图象有何变化,其值域是什么?解:当x∈[-2,3]时,函数的图象为y=x2-2x-3在 [-2,3] 上的一段(图略),且由于f(-2)=5,f(3)=0,因此函数值域为[-4,5].一题多变2:本题(2)中的函数y=x2-2x-3的图象可由 y=x2的图象怎样变化而得到?解:由于y=x2-2x-3=(x-1)2-4,因此该函数图象可由y=x2的图象先沿x轴向右平移1个单位得到y=(x-1)2 的图象后,再沿y轴向下平移4个单位而得到.误区警示作函数图象的步骤及注意点
(1)作函数图象主要有三步:列表、描点、连线.作图象时一般应先确定函数的定义域,再在定义域内化简函数解析式,再列表画出图象.
(2)函数的图象可能是平滑的曲线,也可能是一群孤立的点,画图时要注意关键点,如图象与坐标轴的交点、区间端点、二次函数的顶点等等,还要分清这些关键点是实心点还是空心点.[备用例1] (1)某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程.在图中,纵轴表示离学校的距离,横轴表示出发后的时间,则四个图形中较符合该学生走法的是( )(1)解析:d0随t的增加而减小,故排除选项A,C;又开始一段跑步比走路速度快,排除B.故选D.答案:(1)D(2)如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),
(2,0),(6,4),则f[f(0)]= .?(2)解析:由图象可知f(0)=4,f(4)=2,f[f(0)]=2.答案:(2)2②y=x2-2x+2,x∈(-1,2].(3)解:②y=x2-2x+2=(x-1)2+1,x∈(-1,2],图象如图所示.题型二 函数解析式的求法
[例2] 根据条件求函数解析式:
(1)已知f(x+1)=5x-3,求f(x)的解析式;解:(1)法一 因为5x-3=5(x+1)-8,
所以f(x+1)=5(x+1)-8,
所以f(x)=5x-8.
法二 设t=x+1,则x=t-1,
故f(t)=5(t-1)-3=5t-8,
所以f(x)=5x-8.(2)已知f(x)是关于x的二次函数,且满足f(0)=1,f(x+1)=f(x)+2x,求函数f(x)的解析式;(3)已知f(x)+3f(-x)=x2+2x,求f(x)的解析式.方法技巧求函数解析式的四种常用求法
(1)配凑法:由已知条件f(g(x))=F(x),可将F(x)改写成关于g(x)的表达式,然后以x替代g(x),便得 f(x)的表达式;
(2)待定系数法:若已知函数的类型(如一次函数、二次函数)可用待定系数法;
(3)换元法:已知复合函数f(g(x))的解析式,可用换元法,此时要注意新元的取值范围;(3)已知f(x)是一次函数,且f(x+1)+3f(1-x)=20-4x,求f(x)的解析式.[备用例2] (1)已知二次函数f(x)的二次项系数为a(a>0),且方程f(x)=-2x的两个实数根分别为1和3.若方程f(x)+6a=0有两个相等的实数根,求f(x)的解析式;(2)设f(x)是R上的函数,且满足f(0)=1,并且对任意实数x,y都有f(x-y)
=f(x)-y(2x-y+1),求函数f(x)的解析式;解:(2)法一 因为f(0)=1,
f(x-y)=f(x)-y(2x-y+1),
所以令x=y,得f(0)=f(x)-x(2x-x+1),
所以f(x)=x2+x+1.
法二 令x=0,得f(-y)=f(0)-y(-y+1),
即f(-y)=1-y(-y+1).
又令t=-y,代入上式,得
f(t)=1-(-t)(t+1)=1+t(t+1),
所以f(x)=x2+x+1.(3)已知函数f(x)为二次函数,顶点坐标为(-1,2),且f(0)=3,若g(x)是一次函数,当f[g(x)]=x2+6x+11时,求g(x)的解析式.正解:(1)f(x)=x2-x(x≥2).课堂达标1.购买某种饮料x听,所需钱数为y元,若每听2元,用解析法将y表示成x(x∈{1,2,3,4})的函数为( )
(A)y=2x
(B)y=2x(x∈R)
(C)y=2x(x∈{1,2,3,…})
(D)y=2x(x∈{1,2,3,4})解析:题中已给出自变量的取值范围,x∈{1,2,3,4},故选D.D2.已知函数f(x)由下表给出,则f(3)等于( )解析:由表格可知当x=3时,f(3)=-4.故选D.(A)-1 (B)-2 (C)-3 (D)-4DB 4.已知二次函数的二次项系数为1,该函数图象与x轴有且仅有一个交点(2,0),则此二次函数的解析式为 .?解析:由题意知二次函数对应的二次方程只有一个根x=2,
又二次项系数为1,则f(x)=(x-2)2=x2-4x+4.
答案:f(x)=x2-4x+45.若函数y=f(x)的图象如图所示,则函数f(x)的值域为 .?答案:[-2,3]
第一课时 函数的表示法[目标导航]新知导学·素养养成1.函数的表示方法
解析法,就是用 表示两个变量之间的对应关系.
图象法,就是用 表示两个变量之间的对应关系.
列表法,就是 来表示两个变量之间的对应关系.数学表达式图象列出表格思考1:任何一个函数都可以用解析法表示吗?
答案:不是,并不是所有的函数都可以用解析法表示,如某地区一天中每时每刻的温度,由于受自然影响较大,无法用函数解析式表示.
思考2:函数f(x)=1中无自变量是一个函数解析式吗?
答案:是.该函数的函数值不因自变量的变化而变化,是一个常值函数.2.函数的图象
函数图象既可以是连续的曲线,也可以是直线、折线、离散点等.思考3:函数y=f(x)的图象的集合表示形式是什么?
答案:若y=f(x)的定义域为A,则y=f(x)图象的集合表示形式是{(x,y)|
y=f(x),x∈A}.名师点津(1)对画函数图象三个步骤的认识
①列表:先找出一些有代表性的自变量x的值,并计算出与这些自变量相对应的函数值f(x),用表格的形式表示出来.②描点:把第①步表格中的点(x,f(x))一一在坐标平面上描出来.
③连线:用平滑的曲线把这些点按自变量由小到大的顺序连接起来.(2)函数的表示方法及其优缺点(3)常用的图象变换
①平移变换
a.把函数y=f(x)的图象沿x轴向左(a>0)或向右(a<0)平移|a|个单位长度,就得到函数y=f(x+a)的图象;
b.把函数y=f(x)的图象沿y轴向上(a>0)或向下(a<0)平移|a|个单位长度,就得到函数y=f(x)+a的图象.简记为“上加下减,左加右减”.②对称翻折变换
a.形如y=f(-x)的函数,其函数图象与函数y=f(x)的图象关于y轴对称;
b.形如y=-f(x)的函数,其函数图象与函数y=f(x)的图象关于x轴对称;c.形如y=-f(-x)的函数,其函数图象与函数y=f(x) 的图象关于原点对称;
d.形如y=|f(x)|的函数,将函数y=f(x)的图象在x轴下方的部分沿x轴翻转到x轴上方(下方部分不再保留),x轴上方的图象不变,从而得到函数y=|f(x)|的图象;
e.形如y=f(|x|)的函数,可先作x>0时f(x)的图象,然后将函数y=f(x)的图象y轴右边的部分翻折到y轴左边,y轴右边的图象不变,从而得到函数y=f(|x|)的图象.课堂探究·素养提升题型一 函数图象的作法及应用
[例1] 作下列函数图象并由图象求值域.
(1)y=1-x(x∈Z且|x|≤2);解:(1)函数y=1-x(x∈Z且|x|≤2)的定义域为{-2,-1,0,1,2},
图象为五个点,这些点在直线y=1-x上.
列表所画函数图象如图所示,由图象可知函数值域为{-1,0,1,2,3}.(2)y=x2-2x-3(x∈R);解:(2)函数y=x2-2x-3=(x-1)2-4,
列表所画函数图象如图所示,由图象可知函数值域为{y|y≥-4}.一题多变1:本题(2)中,将x∈R改为x∈[-2,3],则函数图象有何变化,其值域是什么?解:当x∈[-2,3]时,函数的图象为y=x2-2x-3在 [-2,3] 上的一段(图略),且由于f(-2)=5,f(3)=0,因此函数值域为[-4,5].一题多变2:本题(2)中的函数y=x2-2x-3的图象可由 y=x2的图象怎样变化而得到?解:由于y=x2-2x-3=(x-1)2-4,因此该函数图象可由y=x2的图象先沿x轴向右平移1个单位得到y=(x-1)2 的图象后,再沿y轴向下平移4个单位而得到.误区警示作函数图象的步骤及注意点
(1)作函数图象主要有三步:列表、描点、连线.作图象时一般应先确定函数的定义域,再在定义域内化简函数解析式,再列表画出图象.
(2)函数的图象可能是平滑的曲线,也可能是一群孤立的点,画图时要注意关键点,如图象与坐标轴的交点、区间端点、二次函数的顶点等等,还要分清这些关键点是实心点还是空心点.[备用例1] (1)某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程.在图中,纵轴表示离学校的距离,横轴表示出发后的时间,则四个图形中较符合该学生走法的是( )(1)解析:d0随t的增加而减小,故排除选项A,C;又开始一段跑步比走路速度快,排除B.故选D.答案:(1)D(2)如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),
(2,0),(6,4),则f[f(0)]= .?(2)解析:由图象可知f(0)=4,f(4)=2,f[f(0)]=2.答案:(2)2②y=x2-2x+2,x∈(-1,2].(3)解:②y=x2-2x+2=(x-1)2+1,x∈(-1,2],图象如图所示.题型二 函数解析式的求法
[例2] 根据条件求函数解析式:
(1)已知f(x+1)=5x-3,求f(x)的解析式;解:(1)法一 因为5x-3=5(x+1)-8,
所以f(x+1)=5(x+1)-8,
所以f(x)=5x-8.
法二 设t=x+1,则x=t-1,
故f(t)=5(t-1)-3=5t-8,
所以f(x)=5x-8.(2)已知f(x)是关于x的二次函数,且满足f(0)=1,f(x+1)=f(x)+2x,求函数f(x)的解析式;(3)已知f(x)+3f(-x)=x2+2x,求f(x)的解析式.方法技巧求函数解析式的四种常用求法
(1)配凑法:由已知条件f(g(x))=F(x),可将F(x)改写成关于g(x)的表达式,然后以x替代g(x),便得 f(x)的表达式;
(2)待定系数法:若已知函数的类型(如一次函数、二次函数)可用待定系数法;
(3)换元法:已知复合函数f(g(x))的解析式,可用换元法,此时要注意新元的取值范围;(3)已知f(x)是一次函数,且f(x+1)+3f(1-x)=20-4x,求f(x)的解析式.[备用例2] (1)已知二次函数f(x)的二次项系数为a(a>0),且方程f(x)=-2x的两个实数根分别为1和3.若方程f(x)+6a=0有两个相等的实数根,求f(x)的解析式;(2)设f(x)是R上的函数,且满足f(0)=1,并且对任意实数x,y都有f(x-y)
=f(x)-y(2x-y+1),求函数f(x)的解析式;解:(2)法一 因为f(0)=1,
f(x-y)=f(x)-y(2x-y+1),
所以令x=y,得f(0)=f(x)-x(2x-x+1),
所以f(x)=x2+x+1.
法二 令x=0,得f(-y)=f(0)-y(-y+1),
即f(-y)=1-y(-y+1).
又令t=-y,代入上式,得
f(t)=1-(-t)(t+1)=1+t(t+1),
所以f(x)=x2+x+1.(3)已知函数f(x)为二次函数,顶点坐标为(-1,2),且f(0)=3,若g(x)是一次函数,当f[g(x)]=x2+6x+11时,求g(x)的解析式.正解:(1)f(x)=x2-x(x≥2).课堂达标1.购买某种饮料x听,所需钱数为y元,若每听2元,用解析法将y表示成x(x∈{1,2,3,4})的函数为( )
(A)y=2x
(B)y=2x(x∈R)
(C)y=2x(x∈{1,2,3,…})
(D)y=2x(x∈{1,2,3,4})解析:题中已给出自变量的取值范围,x∈{1,2,3,4},故选D.D2.已知函数f(x)由下表给出,则f(3)等于( )解析:由表格可知当x=3时,f(3)=-4.故选D.(A)-1 (B)-2 (C)-3 (D)-4DB 4.已知二次函数的二次项系数为1,该函数图象与x轴有且仅有一个交点(2,0),则此二次函数的解析式为 .?解析:由题意知二次函数对应的二次方程只有一个根x=2,
又二次项系数为1,则f(x)=(x-2)2=x2-4x+4.
答案:f(x)=x2-4x+45.若函数y=f(x)的图象如图所示,则函数f(x)的值域为 .?答案:[-2,3]
