2019_2020学年高中数学第一章集合与函数概念1.3.1单调性与最大(小)值第一课时函数的单调性课件新人教A版必修1:46张PPT
文档属性
| 名称 | 2019_2020学年高中数学第一章集合与函数概念1.3.1单调性与最大(小)值第一课时函数的单调性课件新人教A版必修1:46张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 00:00:00 | ||
图片预览







文档简介
课件46张PPT。1.3 函数的基本性质
1.3.1 单调性与最大(小)值
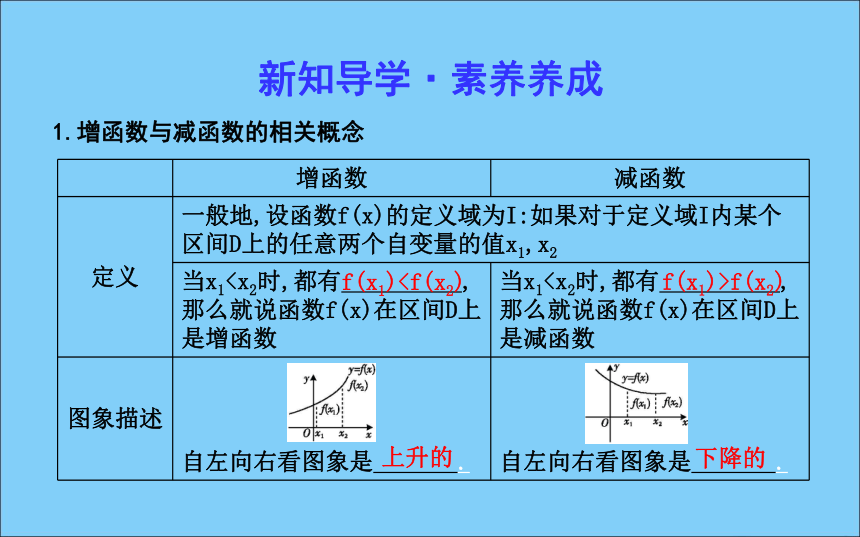
第一课时 函数的单调性[目标导航]新知导学·素养养成1.增函数与减函数的相关概念f(x1)f(x2)上升的下降的2.函数的单调性及单调区间
如果函数y=f(x)在区间D上是 或 ,那么就说函数y=f(x)在这一区间具有(严格的)单调性, 叫做函数y=f(x)的单调区间.思考1:如何理解函数单调性定义中的x1,x2?
答案:(1)任意性,即x1,x2是在某一区间上的任意两个值,不能以特殊值代换;
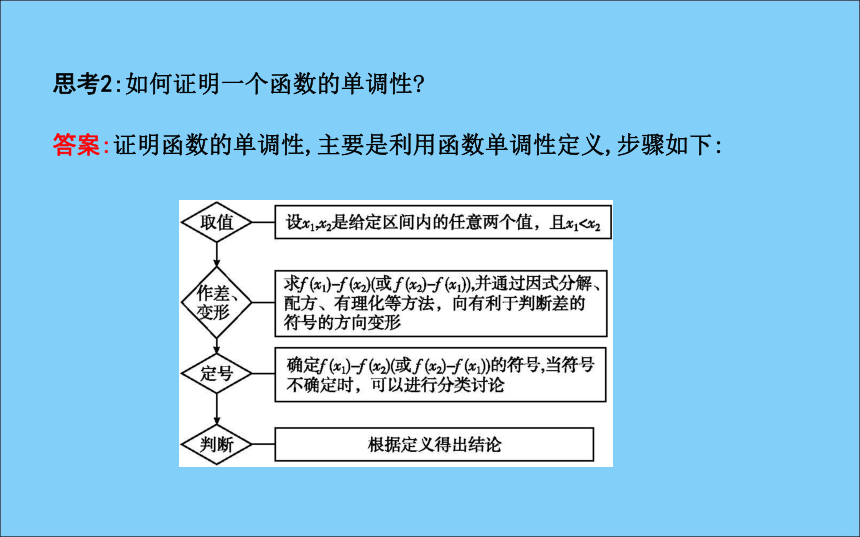
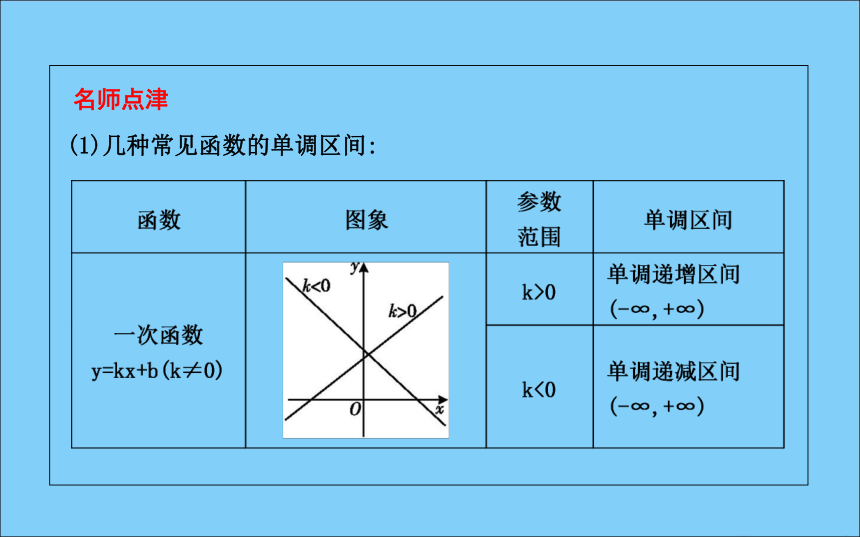
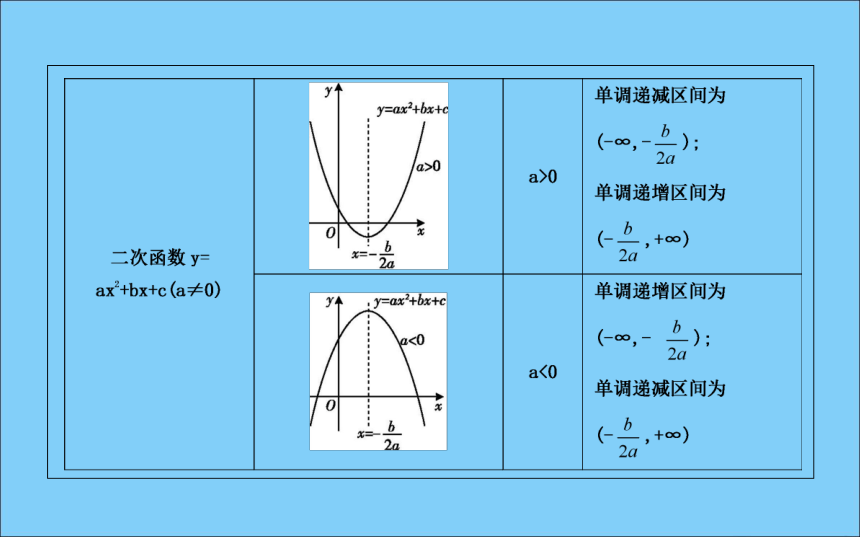
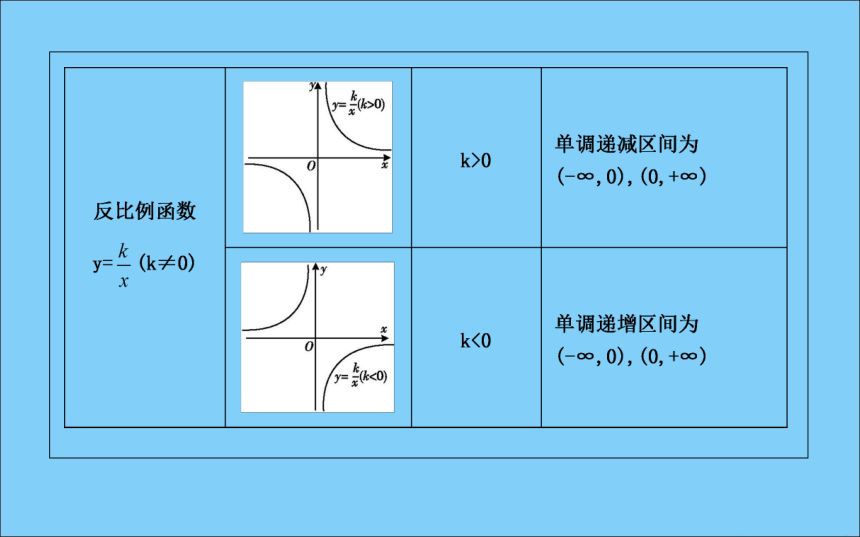
(2)有大小,即确定的两个值x1,x2必须区分大小,一般令x1(3)同属一个单调区间.增函数减函数区间D思考2:如何证明一个函数的单调性?答案:证明函数的单调性,主要是利用函数单调性定义,步骤如下:思考3:函数的单调区间与函数定义域有何关系?当一个函数有多个单调区间时,如何写函数的单调区间.答案:单调区间必须是函数定义域的子集,单调区间之间不能用“∪”,而应用“,”将它们隔开或用“和”字连接.名师点津(1)几种常见函数的单调区间:(2)判断函数单调性的常用结论.
若函数f(x),g(x)在区间I上具有单调性,则:
①f(x)与f(x)+C(C为常数)具有相同的单调性.
②f(x)与a·f(x),当a>0时具有相同的单调性;当 a<0时具有相反的单调性.④在f(x),g(x)的公共单调区间上,有如下结论:⑤当f(x),g(x)都是增(减)函数时,若两者都恒大于零,则f(x)·g(x)也是增(减)函数;若两者都恒小于零,则f(x)·g(x)是减(增)函数.(3)复合函数的单调性
对于复合函数y=f[g(x)],若u=g(x)在给定的区间(a,b)上是单调函数,且y=f(u)在(g(a),g(b))或 (g(b),g(a))上也是单调函数,则复合函数y=f[g(x)] 在(a,b)上是单调函数.
①若u=g(x),y=f(u)在所讨论的区间上都是增函数或都是减函数,则y=f[g(x)]为增函数;②若u=g(x),y=f(u)在所讨论的区间上一个是增函数,另一个是减函数,则y=f[g(x)]为减函数.
列表如下:复合函数的单调性可简记为“同增异减”,即内外层函数的单调性相同时复合函数递增,相异时递减.
注意:对于复合函数y=f[g(x)],内层函数u=g(x)的值域是外层函数y=f(u)的定义域的子集.课堂探究·素养提升方法技巧(1)比较f(x1)与f(x2)的大小常用的方法有“作差,作商”两种,其中差与0比较大小,而商与1比较大小.
(2)常用的变形技巧有:①因式分解.当原函数是多项式函数时,作差后常通过因式分解变形.
②通分.当原函数含有分式时,作差后往往进行通分,然后对分子进行因式分解.
③配方.作差后可以运用配方判断差的符号.
④分子或分母有理化.当函数中含有根式时,作差后主要考虑分子或分母有理化.(3)证明函数f(x)=x3+x在R上是增函数.题型二 求函数的单调区间
[例2] 求函数f(x)=-x2+2|x|+3的单调区间.一题多变:(1)根据例2的方法,求函数f(x)=|x2-2x-3|的单调区间;解:(1)记g(x)=x2-2x-3=(x-1)2-4,
在平面直角坐标系中画出函数g(x)的图象,
将函数g(x)在x轴下方部分的图象翻折到上方即可得到函数f(x)=|g(x)|的图象,如图所示.
因此函数f(x)的单调递增区间是[-1,1],[3,+∞),单调递减区间是(-∞,-1],[1,3].(2)根据例2的方法求函数f(x)=|x2-2|x|-3|的单调区间.方法技巧判断函数单调区间时,若所给函数是常见的一次函数、二次函数、反比例函数等,可根据其单调性写出函数的单调区间,若函数不是上述函数且函数图象容易作出,可作出其图象,根据图象写出函数单调区间.(3)作出函数f(x)=(x+3)|x-2|的图象,并写出函数的单调区间.答案:(1)B (2)若函数f(x)=|2x+a|在[6,+∞)上是增函数,则a的取值范围是 .?答案:(2)[-12,+∞)方法技巧(1)解决此类与抽象函数有关的变量的取值范围问题的关键是利用单调性“脱去”函数符号“f”,从而转化为关于自变量的不等式,常见的转化方法为若函数y=f(x) 在区间D上是增函数,对任意x1,x2∈D,且 f(x1)x2,但需要注意的是不要忘记函数的定义域.即时训练3-1:(1)已知函数f(x)=x2+ax+1,①若f(x)在[-4,+∞)上是增函数,求a的取值范围;②若f(x)的单调递增区间是[-4,+∞),求a的取值;(2)已知函数f(x)是定义在(-∞,0)上的单调递减函数,且f(2x-4)>
f(-2-x).求x的取值范围.②若a>0且f(x)在(1,+∞)上单调递减,求a的取值范围.答案:(-∞,0]答案:(-∞,0]学霸经验分享区课堂达标1.如图中是定义在区间[-5,5]上的函数y=f(x),则下列关于函数f(x)的说法错误的是( )
(A)函数在区间[-5,-3]上单调递增
(B)函数在区间[1,4]上单调递增
(C)函数在区间[-3,1]∪[4,5]上单调递减
(D)函数在区间[-5,5]上没有单调性解析:若一个函数出现两个或两个以上的单调区间时,不能用“∪”连接.故选C.CC 3.若二次函数f(x)=x2+2mx+1在(-∞,1)上是减函数,在(1,+∞)上是增函数,则f(1)等于( )
(A)m2 (B)1 (C)1-m2 (D)0D 解析:由题意知,二次函数对称轴方程为x=1,即-m=1,则m=-1,此时f(x)=x2-2x+1,则f(1)=0.解析:B,C在(0,+∞)上是减函数,而D是二次函数,在(0,1)上是减函数,(1,+∞)上是增函数.故选A.A 5.若函数y=f(x)是定义域为R的增函数,则满足f(2+x)>f(8-2x)的x的取值范围是 .?解析:因为f(x)在R上是增函数,
又因为f(2+x)>f(8-2x),
所以2+x>8-2x,所以x>2.
答案:(2,+∞)
1.3.1 单调性与最大(小)值
第一课时 函数的单调性[目标导航]新知导学·素养养成1.增函数与减函数的相关概念f(x1)
如果函数y=f(x)在区间D上是 或 ,那么就说函数y=f(x)在这一区间具有(严格的)单调性, 叫做函数y=f(x)的单调区间.思考1:如何理解函数单调性定义中的x1,x2?
答案:(1)任意性,即x1,x2是在某一区间上的任意两个值,不能以特殊值代换;
(2)有大小,即确定的两个值x1,x2必须区分大小,一般令x1
若函数f(x),g(x)在区间I上具有单调性,则:
①f(x)与f(x)+C(C为常数)具有相同的单调性.
②f(x)与a·f(x),当a>0时具有相同的单调性;当 a<0时具有相反的单调性.④在f(x),g(x)的公共单调区间上,有如下结论:⑤当f(x),g(x)都是增(减)函数时,若两者都恒大于零,则f(x)·g(x)也是增(减)函数;若两者都恒小于零,则f(x)·g(x)是减(增)函数.(3)复合函数的单调性
对于复合函数y=f[g(x)],若u=g(x)在给定的区间(a,b)上是单调函数,且y=f(u)在(g(a),g(b))或 (g(b),g(a))上也是单调函数,则复合函数y=f[g(x)] 在(a,b)上是单调函数.
①若u=g(x),y=f(u)在所讨论的区间上都是增函数或都是减函数,则y=f[g(x)]为增函数;②若u=g(x),y=f(u)在所讨论的区间上一个是增函数,另一个是减函数,则y=f[g(x)]为减函数.
列表如下:复合函数的单调性可简记为“同增异减”,即内外层函数的单调性相同时复合函数递增,相异时递减.
注意:对于复合函数y=f[g(x)],内层函数u=g(x)的值域是外层函数y=f(u)的定义域的子集.课堂探究·素养提升方法技巧(1)比较f(x1)与f(x2)的大小常用的方法有“作差,作商”两种,其中差与0比较大小,而商与1比较大小.
(2)常用的变形技巧有:①因式分解.当原函数是多项式函数时,作差后常通过因式分解变形.
②通分.当原函数含有分式时,作差后往往进行通分,然后对分子进行因式分解.
③配方.作差后可以运用配方判断差的符号.
④分子或分母有理化.当函数中含有根式时,作差后主要考虑分子或分母有理化.(3)证明函数f(x)=x3+x在R上是增函数.题型二 求函数的单调区间
[例2] 求函数f(x)=-x2+2|x|+3的单调区间.一题多变:(1)根据例2的方法,求函数f(x)=|x2-2x-3|的单调区间;解:(1)记g(x)=x2-2x-3=(x-1)2-4,
在平面直角坐标系中画出函数g(x)的图象,
将函数g(x)在x轴下方部分的图象翻折到上方即可得到函数f(x)=|g(x)|的图象,如图所示.
因此函数f(x)的单调递增区间是[-1,1],[3,+∞),单调递减区间是(-∞,-1],[1,3].(2)根据例2的方法求函数f(x)=|x2-2|x|-3|的单调区间.方法技巧判断函数单调区间时,若所给函数是常见的一次函数、二次函数、反比例函数等,可根据其单调性写出函数的单调区间,若函数不是上述函数且函数图象容易作出,可作出其图象,根据图象写出函数单调区间.(3)作出函数f(x)=(x+3)|x-2|的图象,并写出函数的单调区间.答案:(1)B (2)若函数f(x)=|2x+a|在[6,+∞)上是增函数,则a的取值范围是 .?答案:(2)[-12,+∞)方法技巧(1)解决此类与抽象函数有关的变量的取值范围问题的关键是利用单调性“脱去”函数符号“f”,从而转化为关于自变量的不等式,常见的转化方法为若函数y=f(x) 在区间D上是增函数,对任意x1,x2∈D,且 f(x1)
f(-2-x).求x的取值范围.②若a>0且f(x)在(1,+∞)上单调递减,求a的取值范围.答案:(-∞,0]答案:(-∞,0]学霸经验分享区课堂达标1.如图中是定义在区间[-5,5]上的函数y=f(x),则下列关于函数f(x)的说法错误的是( )
(A)函数在区间[-5,-3]上单调递增
(B)函数在区间[1,4]上单调递增
(C)函数在区间[-3,1]∪[4,5]上单调递减
(D)函数在区间[-5,5]上没有单调性解析:若一个函数出现两个或两个以上的单调区间时,不能用“∪”连接.故选C.CC 3.若二次函数f(x)=x2+2mx+1在(-∞,1)上是减函数,在(1,+∞)上是增函数,则f(1)等于( )
(A)m2 (B)1 (C)1-m2 (D)0D 解析:由题意知,二次函数对称轴方程为x=1,即-m=1,则m=-1,此时f(x)=x2-2x+1,则f(1)=0.解析:B,C在(0,+∞)上是减函数,而D是二次函数,在(0,1)上是减函数,(1,+∞)上是增函数.故选A.A 5.若函数y=f(x)是定义域为R的增函数,则满足f(2+x)>f(8-2x)的x的取值范围是 .?解析:因为f(x)在R上是增函数,
又因为f(2+x)>f(8-2x),
所以2+x>8-2x,所以x>2.
答案:(2,+∞)
