2019_2020学年高中数学第一章集合与函数概念章末总结课件新人教A版必修1:40张PPT
文档属性
| 名称 | 2019_2020学年高中数学第一章集合与函数概念章末总结课件新人教A版必修1:40张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 556.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 12:46:48 | ||
图片预览









文档简介
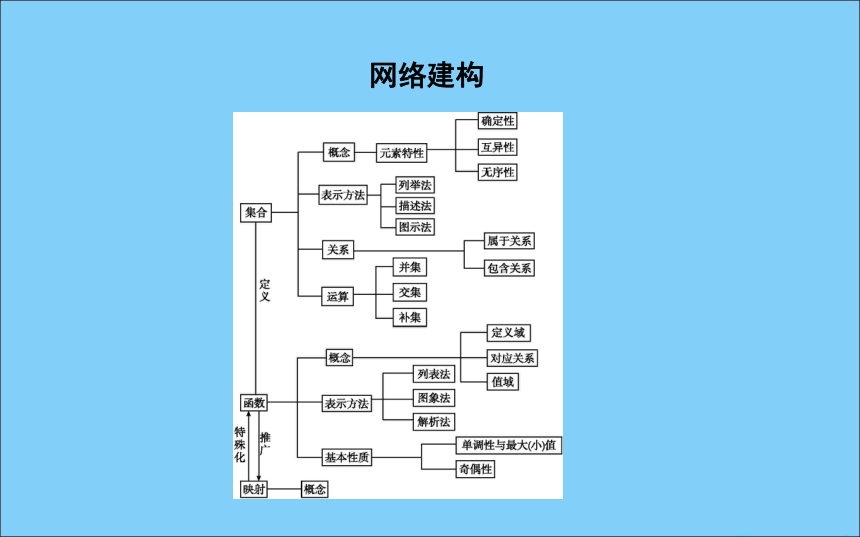
课件40张PPT。章末总结网络建构1.集合中的元素具有确定性.( )
2.任何一个集合有两个或两个以上的子集.( )
3.A∩B?A,A?A∪B.( )
4.若非空数集f:A→B能构成函数,且该函数的值域是C,则C=B.( )
5.函数一定是映射,但映射不一定是函数.( )
6.在增函数与减函数的定义中,可以把“任意两个自变量”改为“存在两个自变量”.( )
7.任何函数都具有单调性.( )知识辨析判断下列说法是否正确(请在括号中填“√”或“×”)√×√×√××8.奇偶函数的定义域关于原点对称.( )
9.若y=f(x)是奇函数,则一定有f(0)=0.( )
10.若函数y=f(x)是偶函数,则f(-x)=f(x)=f(|x|).( )
11.奇函数在关于原点对称的两个区间上单调性相同,偶函数在关于原点对称的两个区间上单调性相反.( )
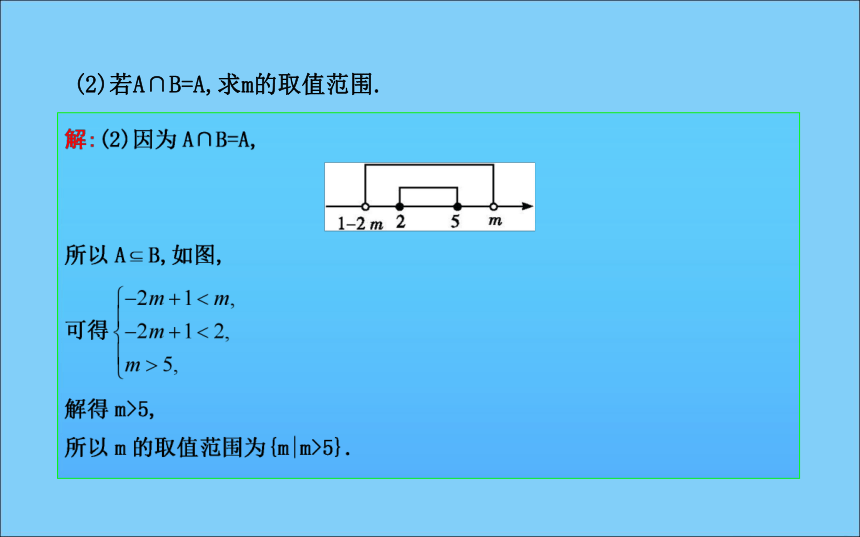
12.若一个图形关于y轴对称,则它一定是偶函数的图象.( )√×√√×题型归纳·素养提升真题体验·素养升级题型归纳·素养提升题型一 集合间的关系及运算[典例1] 已知集合A={x|2≤x≤5},B={x|-2m+1(1)若m=3,求A∪B和(?RA)∩B;解:(1)因为m=3,
所以B={x|-5又因为A={x|2≤x≤5}.
所以?RA={x|x<2或x>5},A∪B={x|-5所以(?RA)∩B={x|-5所以-5≤2x+3<13,
故f(x)的定义域为[-5,13),
则函数f(2x-3)的定义域满足-5≤2x-3<13.
所以-1≤x<8,
所以f(2x-3)的定义域是[-1,8).答案:(3)[-1,8)规律方法(1)判断某一对应关系是否为函数的步骤:
①A,B为非空数集;
②A中任一元素在B中有元素与之对应;
③B中与A中元素对应的元素唯一.
满足上述三条,则对应关系是函数关系.
(2)求函数的定义域,对于已知函数解析式求定义域问题,就是使解析式有意义的自变量x的范围;复合函数求定义域要明确中间变量是什么,定义域仍然是解析式中自变量的取值范围.题型三 求函数解析式[典例3] (1)已知2f(x-1)-f(1-x)=2x2-1,求二次函数f(x)的解析式;规律方法(1)已知函数解析式的特征,求函数解析式一般利用待定系数法,本题(1)中由于函数为二次函数,因此可设为f(x)=ax2+bx+c(a≠0),利用待定系数法求a,b,c.
(2)本题(2)中的求解可用换元法,但要注意新元的范围.题型四 求函数的最值
[典例4] (2019·江苏省常熟市高一上期中)已知f(x)是二次函数,f(0)=f(5)=0,且f(-1)=12.
(1)求f(x)的解析式;解:(1)因为f(x)是二次函数,且f(0)=f(5)=0,
所以设f(x)=ax(x-5)(a≠0),
又因为f(-1)=6a=12,所以a=2,
所以f(x)=2x(x-5)=2x2-10x.(2)求f(x)在[0,m]的最小值g(m);(3)对(2)中的g(m),求不等式g(t)(1)充分利用已知的条件,结合函数的奇偶性,把已知不等式转化为f(x1)>f(x2)或f(x1)(2)在对称区间上根据奇函数的单调性一致,偶函数的单调性相反,列出不等式或不等式组,求解即可,同时要注意函数自身定义域对参数的影响.题型六 恒成立问题
[典例6] (2019·河北省廊坊市省级示范高中联合体高一上期中)二次函数f(x)满足f(x)=f(-x)+12x+f(0)-6,且f(-1)=1.
(1)求f(x)的解析式;(2)当x∈[-3,0]时,不等式f(2x)>4x+m恒成立,求m的取值范围.解:(2)由(1)及f(2x)>4x+m,得4x2+8x+6>m,
令g(x)=4x2+8x+6,x∈[-3,0],
所以当x=-1时,g(x)min=g(-1)=2,
从而要使不等式f(2x)>4x+m恒成立,则m<2.规律方法涉及与最值有关的恒成立问题的主要解题思路是:
若a≥f(x)恒成立,则a≥f(x)max;
若a≤f(x)恒成立,则a≤f(x)min.题型七 抽象函数性质问题
[典例7] 定义在非零实数集上的函数f(x)满足:f(xy)=f(x)+f(y),且f(x)在区间(0,+∞)上为递增函数.
(1)求f(1)、f(-1)的值;(1)解:因为f(xy)=f(x)+f(y),
所以f(1×1)=f(1)+f(1),
所以f(1)=0,
又f[(-1)×(-1)]=f(1)=f(-1)+f(-1),
所以f(-1)=0.(2)求证:f(x)是偶函数;(2)证明:因为f(xy)=f(x)+f(y),
所以f(-x)=f(-1)+f(x)=f(x),
所以f(x)是偶函数.规律方法求解与抽象函数有关的求值问题应恰当地使用“赋值法”,而涉及抽象函数奇偶性判断问题,应准确构造出 f(-x)与f(x)后判断其关系.题型八 易错题辨析
[典例8] 已知f(x)是定义在R上的偶函数,且在(0,+∞)上是增函数,若f(2 019)=0,则f(x)>0的解集是 .?错解:因为f(x)>0且f(2 019)=0,
所以f(x)>f(2 019).
又f(x)是(0,+∞)上的增函数.
所以x>2 019.纠错:由于y=f(x)是R上的偶函数,因此函数y=f(x)在(-∞,0)上是减函数,上述求解过程忽视了偶函数的性质.
正解:因为f(x)是R上的偶函数,
所以f(-x)=f(x)=f(|x|).
又f(x)在(0,+∞)上是增函数且f(2 019)=0.
所以f(x)>f(2 019),即f(|x|)>f(2 019).
所以|x|>2 019.
所以x>2 019或x<-2 019.
答案:(-∞,-2 019)∪(2 019,+∞)纠错:错解对集合B中元素的特征性质进行了不等价变形,从而导致结论错误.真题体验·素养升级1.(2018·全国Ⅱ卷)已知集合A={1,3,5,7},B={2,3,4,5},则A∩B等于( )
(A){3} (B){5}
(C){3,5} (D){1,2,3,4,5,7}C解析:A∩B={1,3,5,7}∩{2,3,4,5}={3,5}.故选C.2.(2018·全国Ⅱ卷)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为( )
(A)9 (B)8 (C)5 (D)4A解析:将满足x2+y2≤3的整数x,y全部列举出来,即(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1),共有9个.故选A.3.(2018·全国Ⅰ卷)已知集合A={x|x2-x-2>0},则 ?RA 等于( )
(A){x|-1(B){x|-1≤x≤2}
(C){x|x<-1}∪{x|x>2}
(D){x|x≤-1}∪{x|x≥2}B解析:因为A={x|x2-x-2>0},
所以?RA={x|x2-x-2≤0}={x|-1≤x≤2},故选B.4.(2018·天津卷)设集合A={1,2,3,4},B={-1,0,2,3},C={x∈R|-1≤x<2},则(A∪B)∩C等于( )
(A){-1,1} (B){0,1}
(C){-1,0,1} (D){2,3,4}C解析:因为A={1,2,3,4},B={-1,0,2,3},
所以A∪B={-1,0,1,2,3,4}.
又C={x∈R|-1≤x<2},
所以(A∪B)∩C={-1,0,1}.故选C.5.(2017·全国Ⅰ卷)函数f(x)在(-∞,+∞)单调递减,且为奇函数,若f(1)=-1,则满足-1≤f(x-2)≤1的x取值范围是( )
(A)[-2,2] (B)[-1,1] (C)[0,4] (D)[1,3]D解析:因为f(x)是奇函数且f(1)=-1,
所以f(-1)=-f(1)=1,
所以-1≤f(x-2)≤1,
即f(1)≤f(x-2)≤f(-1).
又因为f(x)在(-∞,+∞)上单调递减,
所以-1≤x-2≤1,
所以1≤x≤3.故选D.6.(2017·全国Ⅱ卷)已知函数f(x)是定义在R上的奇函数,当x∈(-∞,0)时,f(x)=2x3+x2,则f(2)= .?解析:因为x∈(-∞,0),f(x)=2x3+x2且为奇函数,
所以f(-2)=2×(-8)+4=-12,
又因为f(-2)=-f(2)=-12,
所以f(2)=12.答案:12
2.任何一个集合有两个或两个以上的子集.( )
3.A∩B?A,A?A∪B.( )
4.若非空数集f:A→B能构成函数,且该函数的值域是C,则C=B.( )
5.函数一定是映射,但映射不一定是函数.( )
6.在增函数与减函数的定义中,可以把“任意两个自变量”改为“存在两个自变量”.( )
7.任何函数都具有单调性.( )知识辨析判断下列说法是否正确(请在括号中填“√”或“×”)√×√×√××8.奇偶函数的定义域关于原点对称.( )
9.若y=f(x)是奇函数,则一定有f(0)=0.( )
10.若函数y=f(x)是偶函数,则f(-x)=f(x)=f(|x|).( )
11.奇函数在关于原点对称的两个区间上单调性相同,偶函数在关于原点对称的两个区间上单调性相反.( )
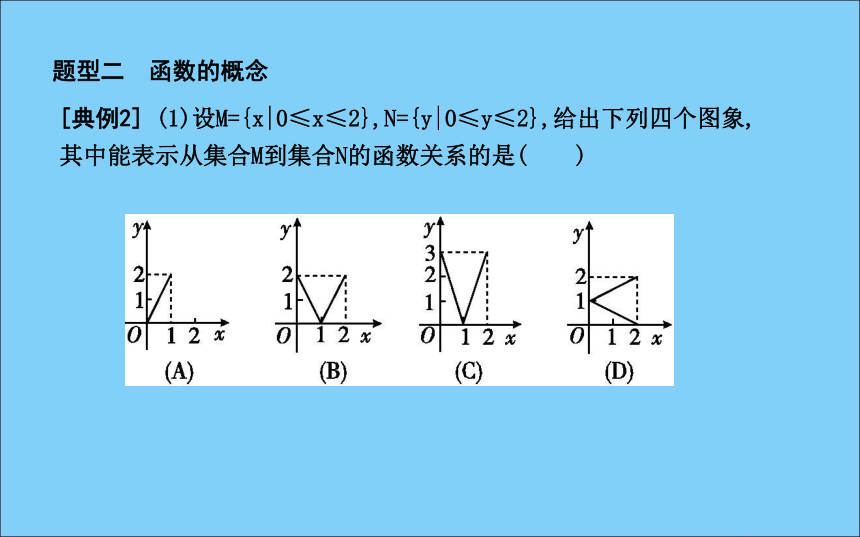
12.若一个图形关于y轴对称,则它一定是偶函数的图象.( )√×√√×题型归纳·素养提升真题体验·素养升级题型归纳·素养提升题型一 集合间的关系及运算[典例1] 已知集合A={x|2≤x≤5},B={x|-2m+1
所以B={x|-5
所以?RA={x|x<2或x>5},A∪B={x|-5
故f(x)的定义域为[-5,13),
则函数f(2x-3)的定义域满足-5≤2x-3<13.
所以-1≤x<8,
所以f(2x-3)的定义域是[-1,8).答案:(3)[-1,8)规律方法(1)判断某一对应关系是否为函数的步骤:
①A,B为非空数集;
②A中任一元素在B中有元素与之对应;
③B中与A中元素对应的元素唯一.
满足上述三条,则对应关系是函数关系.
(2)求函数的定义域,对于已知函数解析式求定义域问题,就是使解析式有意义的自变量x的范围;复合函数求定义域要明确中间变量是什么,定义域仍然是解析式中自变量的取值范围.题型三 求函数解析式[典例3] (1)已知2f(x-1)-f(1-x)=2x2-1,求二次函数f(x)的解析式;规律方法(1)已知函数解析式的特征,求函数解析式一般利用待定系数法,本题(1)中由于函数为二次函数,因此可设为f(x)=ax2+bx+c(a≠0),利用待定系数法求a,b,c.
(2)本题(2)中的求解可用换元法,但要注意新元的范围.题型四 求函数的最值
[典例4] (2019·江苏省常熟市高一上期中)已知f(x)是二次函数,f(0)=f(5)=0,且f(-1)=12.
(1)求f(x)的解析式;解:(1)因为f(x)是二次函数,且f(0)=f(5)=0,
所以设f(x)=ax(x-5)(a≠0),
又因为f(-1)=6a=12,所以a=2,
所以f(x)=2x(x-5)=2x2-10x.(2)求f(x)在[0,m]的最小值g(m);(3)对(2)中的g(m),求不等式g(t)
[典例6] (2019·河北省廊坊市省级示范高中联合体高一上期中)二次函数f(x)满足f(x)=f(-x)+12x+f(0)-6,且f(-1)=1.
(1)求f(x)的解析式;(2)当x∈[-3,0]时,不等式f(2x)>4x+m恒成立,求m的取值范围.解:(2)由(1)及f(2x)>4x+m,得4x2+8x+6>m,
令g(x)=4x2+8x+6,x∈[-3,0],
所以当x=-1时,g(x)min=g(-1)=2,
从而要使不等式f(2x)>4x+m恒成立,则m<2.规律方法涉及与最值有关的恒成立问题的主要解题思路是:
若a≥f(x)恒成立,则a≥f(x)max;
若a≤f(x)恒成立,则a≤f(x)min.题型七 抽象函数性质问题
[典例7] 定义在非零实数集上的函数f(x)满足:f(xy)=f(x)+f(y),且f(x)在区间(0,+∞)上为递增函数.
(1)求f(1)、f(-1)的值;(1)解:因为f(xy)=f(x)+f(y),
所以f(1×1)=f(1)+f(1),
所以f(1)=0,
又f[(-1)×(-1)]=f(1)=f(-1)+f(-1),
所以f(-1)=0.(2)求证:f(x)是偶函数;(2)证明:因为f(xy)=f(x)+f(y),
所以f(-x)=f(-1)+f(x)=f(x),
所以f(x)是偶函数.规律方法求解与抽象函数有关的求值问题应恰当地使用“赋值法”,而涉及抽象函数奇偶性判断问题,应准确构造出 f(-x)与f(x)后判断其关系.题型八 易错题辨析
[典例8] 已知f(x)是定义在R上的偶函数,且在(0,+∞)上是增函数,若f(2 019)=0,则f(x)>0的解集是 .?错解:因为f(x)>0且f(2 019)=0,
所以f(x)>f(2 019).
又f(x)是(0,+∞)上的增函数.
所以x>2 019.纠错:由于y=f(x)是R上的偶函数,因此函数y=f(x)在(-∞,0)上是减函数,上述求解过程忽视了偶函数的性质.
正解:因为f(x)是R上的偶函数,
所以f(-x)=f(x)=f(|x|).
又f(x)在(0,+∞)上是增函数且f(2 019)=0.
所以f(x)>f(2 019),即f(|x|)>f(2 019).
所以|x|>2 019.
所以x>2 019或x<-2 019.
答案:(-∞,-2 019)∪(2 019,+∞)纠错:错解对集合B中元素的特征性质进行了不等价变形,从而导致结论错误.真题体验·素养升级1.(2018·全国Ⅱ卷)已知集合A={1,3,5,7},B={2,3,4,5},则A∩B等于( )
(A){3} (B){5}
(C){3,5} (D){1,2,3,4,5,7}C解析:A∩B={1,3,5,7}∩{2,3,4,5}={3,5}.故选C.2.(2018·全国Ⅱ卷)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为( )
(A)9 (B)8 (C)5 (D)4A解析:将满足x2+y2≤3的整数x,y全部列举出来,即(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1),共有9个.故选A.3.(2018·全国Ⅰ卷)已知集合A={x|x2-x-2>0},则 ?RA 等于( )
(A){x|-1
(C){x|x<-1}∪{x|x>2}
(D){x|x≤-1}∪{x|x≥2}B解析:因为A={x|x2-x-2>0},
所以?RA={x|x2-x-2≤0}={x|-1≤x≤2},故选B.4.(2018·天津卷)设集合A={1,2,3,4},B={-1,0,2,3},C={x∈R|-1≤x<2},则(A∪B)∩C等于( )
(A){-1,1} (B){0,1}
(C){-1,0,1} (D){2,3,4}C解析:因为A={1,2,3,4},B={-1,0,2,3},
所以A∪B={-1,0,1,2,3,4}.
又C={x∈R|-1≤x<2},
所以(A∪B)∩C={-1,0,1}.故选C.5.(2017·全国Ⅰ卷)函数f(x)在(-∞,+∞)单调递减,且为奇函数,若f(1)=-1,则满足-1≤f(x-2)≤1的x取值范围是( )
(A)[-2,2] (B)[-1,1] (C)[0,4] (D)[1,3]D解析:因为f(x)是奇函数且f(1)=-1,
所以f(-1)=-f(1)=1,
所以-1≤f(x-2)≤1,
即f(1)≤f(x-2)≤f(-1).
又因为f(x)在(-∞,+∞)上单调递减,
所以-1≤x-2≤1,
所以1≤x≤3.故选D.6.(2017·全国Ⅱ卷)已知函数f(x)是定义在R上的奇函数,当x∈(-∞,0)时,f(x)=2x3+x2,则f(2)= .?解析:因为x∈(-∞,0),f(x)=2x3+x2且为奇函数,
所以f(-2)=2×(-8)+4=-12,
又因为f(-2)=-f(2)=-12,
所以f(2)=12.答案:12
