人教版六上第5单元第4课时《圆的面积-解决问题》同步练习(含答案及解析)
文档属性
| 名称 | 人教版六上第5单元第4课时《圆的面积-解决问题》同步练习(含答案及解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 684.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-24 00:00:00 | ||
图片预览



文档简介
第五单元第4课时《圆的面积-解决问题》同步练习
1、大圆的半径等于小圆的直径,则大圆的面积是小圆的( )倍。
A. 2 B.4 C.8
2、一个圆的周长扩大3倍,面积就扩大( )倍。
A.3 B.6 C.9
3、在一个长为7厘米,宽为4厘米的长方形纸上剪一个直径为2厘米的圆,最多可以剪( )个这样的圆。
A.4 B. 6 C.8
4、圆的半径由6厘米增加了3厘米,则圆的面积增加了( )cm? 。
A. 9π B. 45π C.81π
5、圆的半径由3cm增加到4cm,则圆的面积增加了( )cm 。
A.3.14 B.6.28 C.21.98
6、一个圆的周长是6.28m,它的面积是( )m? 。
A.3.14 B.6.28 C.0.785
7、一个圆的半径扩大4倍,那么它的面积( )
A.扩大4倍 B.扩大8倍 C.扩大16倍
8、一个环形内圆半径为14厘米,外圆半径为18厘米,环形面积是( )
A.128π B.64π C.196π D.32π
9、如图,已知正方形的面积是36cm2,圆的面积是( )
A.9πcm2 B.18πcm2 C.36πcm2
10、一个圆形水池周长是31.4米,在它周围修一条1米宽的水泥路,水泥路面积是( )平方米.
A.34.54 B.65.94 C.3.14
二、填一填。
(1)如果圆的半径扩大到原来的2倍,那么直径扩大到原来的( )倍,周长扩大到原来的( )倍,面积扩大到原来的( )倍。
(2)如果一个环形的外圆半径用R表示,小圆半径用r表示,则圆环的面积
S=( )
(3)在一个长6厘米,宽4厘米的长方形内画一个最大的圆,这个圆的面积是( )平方厘米.
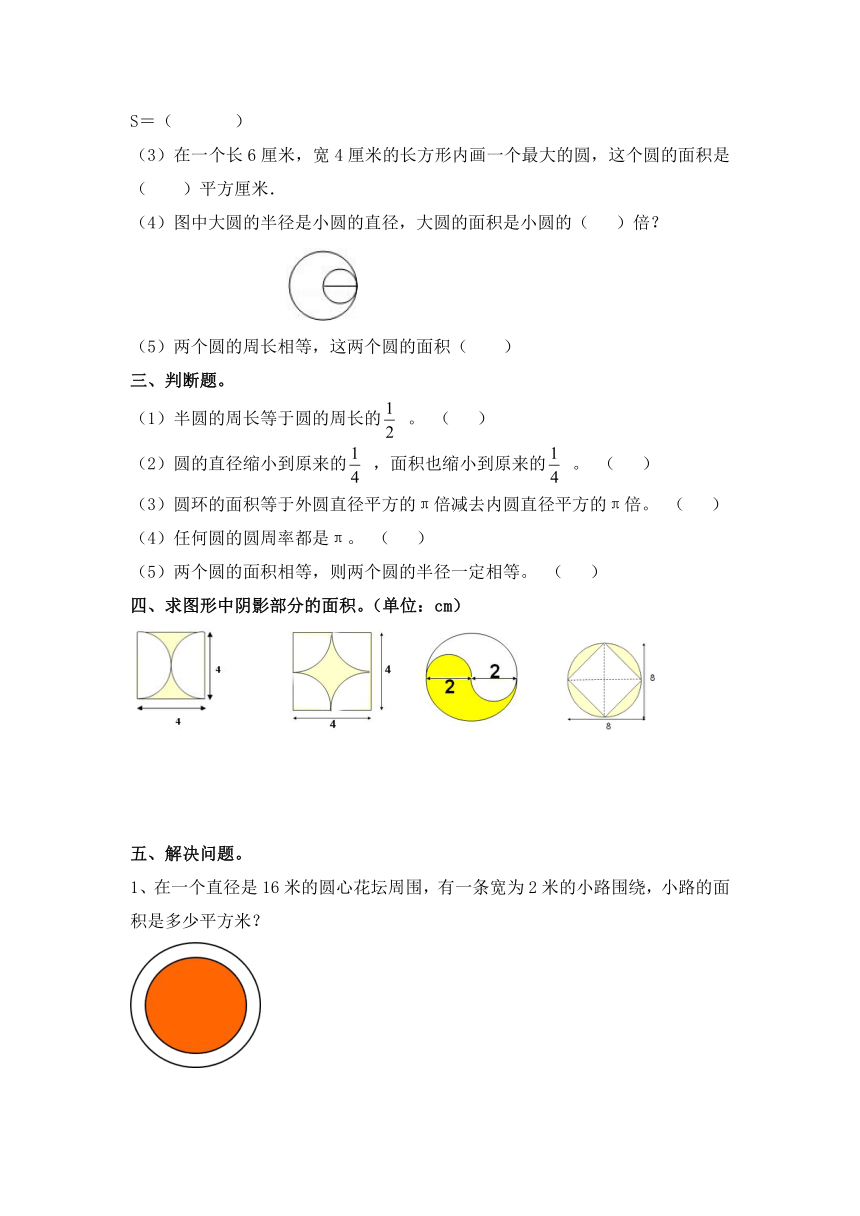
(4)图中大圆的半径是小圆的直径,大圆的面积是小圆的( )倍?
(5)两个圆的周长相等,这两个圆的面积( )
三、判断题。
(1)半圆的周长等于圆的周长的 。 ( )
(2)圆的直径缩小到原来的 ,面积也缩小到原来的 。 ( )
(3)圆环的面积等于外圆直径平方的π倍减去内圆直径平方的π倍。 ( )
(4)任何圆的圆周率都是π。 ( )
(5)两个圆的面积相等,则两个圆的半径一定相等。 ( )
四、求图形中阴影部分的面积。(单位:cm)
五、解决问题。
1、在一个直径是16米的圆心花坛周围,有一条宽为2米的小路围绕,小路的面积是多少平方米?
2、一个水缸,从里面量,缸口直径是 50厘米,缸壁厚 5厘米。要制做一个缸盖,使它正好盖住缸口的外沿,这个缸盖的面积是多少平方厘米?如果在缸盖的边沿贴上一圈金属(不计接头),这个金属条长多少厘米
3、在一张长为3米,宽为2米的长方形铁板上切割出一个最大的圆,剩下的面积是多少平方米?
4、碾是劳动人民智慧的结晶之一,在漫长的历史长河中起着巨大的作用。图中的这台碾安置在长为8米,宽为5米的房间里,碾台半径是0.8米,碾杆超出碾台1米,这个房间的安全区域(碾杆转一圈扫过的面积以外的部分)是多少平方米?
六、拓展提升。
我国古代有“天圆如张盖,地方如棋局”的说法。虽然这种说法是错误的,却产生了深远的影响,尤其体现在建筑设计上。下图是在中国建筑中经常见到的“外方内圆”和“外圆内方”的设计。假如这两个圆的半径都是0.8米,你知道哪个图形中正方形和圆之间部分的面积会大一些吗?
参考答案
1、
【答案】B
【解析】设大圆的半径为R,小圆的直径为d,半径为r,由题意知:
R=d=2r,根据圆的面积公式,大圆面积=π=π=4π,小圆面积=π,
所以大圆的面积是小圆的4倍.
2、
【答案】C
【解析】 由C=2πr可知,周长扩大3倍,半径也扩大 3倍,而面积=π,因此面积就扩大9倍。
3、
【答案】B
【解析】长可剪:7÷2≈3(个),宽可剪:4÷2=2(个),因此,最多可剪:3×2=6(个)。
4、
【答案】B
【解析】增加后的半径为9厘米,π×9?-π×6?=45π(平分厘米)
5、
【答案】C
【解析】用半径为4的圆的面积减去半径为3的圆的面积即可。
6、
【答案】A
【解析】利用周长先求半径,r===1,所以面积=3.14×1=3.14m?。
7、
【答案】C
【解析】设圆的半径为r,则扩大4倍后的半径为4r,利用圆的面积公式分别求出原来和现在的面积,即可求得扩大的倍数.
8、
【答案】A
【解析】根据圆环的面积公式:圆环的面积=π(R?﹣r?),计算即可求解.
9、
【答案】A 【解析】因为6×6=36,所以这个正方形的边长是6厘米,则圆的直径就是6厘米,圆的面积S=πr2,据此代入公式即可答案.
10、
【答案】A
【解析】根据环形面积=外圆面积﹣内圆面积,首先根据圆的周长公式:c=2πr,已知圆形水池的周长是31.4米,求出水池的半径,水池的半径加上1米就是外圆的半径,把数据代入环形面积公式S=π(R2﹣r2)答案即可.
水池的半径:
31.4÷3.14÷2=5(米),
水泥路的面积:
3.14×[(5+1)2﹣52]
=3.14×[36﹣25]
=3.14×11
=34.54(平方米).
二、填一填。
(1)
【答案】2、2、4
【解析】d=2r,周长=2d,面积=π,利用它们之间的关系即可解答。
(2)
【答案】π(R-r)
【解析】外圆面积减去小圆面积即可。
(3)
【答案】12.56
【解析】长方形内最大的圆的直径等于长方形的最短边4厘米,据此利用圆的面积公式计算即可.3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
(4)
【答案】4
【解析】大圆的半径等于小圆直径,即大圆的半径是小圆的半径的2倍;设小圆的半径为r,则大圆的半径就是2r,利用圆的面积公式即可分别求得大小圆的面积的倍数关系.
【答案】C
(5)
【解析】根据圆的周长公式可知两个圆的周长相等,则两个圆的半径相等,再根据圆的面积公式可知两个圆的半径相等,两个圆的面积就相等,再作出选择即可.
三、判断题。
(1)
【答案】错误
【解析】半圆的周长=圆的周长的一半+直径
(2)
【答案】错误
【解析】直径缩小到原来的,半径也缩小到原来的,则面积就缩小到原来的
(3)
【答案】错误
【解析】圆环的面积=π(R-r)
4)
【答案】正确
【解析】π是圆的周长与直径的比,是一个定值。
(5)
【答案】正确
【解析】圆面积=π,由于π是定值,面积相等,r一定相等。
四、求图形中阴影部分的面积。(单位:cm)
【答案】3.44;3.44;6.28;18.24
【解析】(1)4×4-3.14×2
=3.44(cm)
(2)4×4-3.14×2
=3.44(cm)
(3)×3.14×2
=6.28(cm)
(4)3.14×4-(×8×4)×2
=18.24(cm)
五、解决问题。
1、
【答案】3.14×(10-8)
=113.04(平方米)
【解析】外圆半径是:10米,内圆半径是:8米
小路面积是:3.14×(10-8)=113.04(平方米)
2、
【答案】3.14×30=2826(平方厘米);2×3.14×30=188.4(厘米)
【解析】(1)缸口外面的半径是30厘米
缸盖的面积是:3.14×30=2826(平方厘米)
(2)利用周长公式计算即可。
3、
【答案】2×3-3.14×1
=2.86(平方米)
【解析】由于长方形的宽为2米,所以最大圆的半径只能为1,剩下的面积=长方形的面积-圆的面积。
4、
【答案】5×8-3.14×(1+0.8)
=29.8264(平方米)
【解析】用房间的面积减去碾杆扫过的区域的面积就是安全区域的面积。
六、拓展提升。
【答案】第2个图形
【解析】
图(1) 图(2)
要想知道哪个图形中正方形和圆之间部分的面积会大一些,首先要求出每个图
形中正方形和圆之间部分的面积,然后再比大小。
从图(1)可以看出:正方形的面积是:1.6×1.6=2.56(m)
圆的面积是:3.14×0.8=2.0096(m),则正方形和圆之间部分的面积是:
2.56-2.0096=0.5504(m)
从图(2)可以看出:圆的面积是:3.14×0.8=2.0096(m),正方形的面积是:(×0.8×0.8)×4=1.28(m)则正方形和圆之间部分的面积是:2.0096-1.28=0.7296(m)。因为0.5504<0.7296,所以第2个图形中正方形和圆之间部分的面积要大一些。
1、大圆的半径等于小圆的直径,则大圆的面积是小圆的( )倍。
A. 2 B.4 C.8
2、一个圆的周长扩大3倍,面积就扩大( )倍。
A.3 B.6 C.9
3、在一个长为7厘米,宽为4厘米的长方形纸上剪一个直径为2厘米的圆,最多可以剪( )个这样的圆。
A.4 B. 6 C.8
4、圆的半径由6厘米增加了3厘米,则圆的面积增加了( )cm? 。
A. 9π B. 45π C.81π
5、圆的半径由3cm增加到4cm,则圆的面积增加了( )cm 。
A.3.14 B.6.28 C.21.98
6、一个圆的周长是6.28m,它的面积是( )m? 。
A.3.14 B.6.28 C.0.785
7、一个圆的半径扩大4倍,那么它的面积( )
A.扩大4倍 B.扩大8倍 C.扩大16倍
8、一个环形内圆半径为14厘米,外圆半径为18厘米,环形面积是( )
A.128π B.64π C.196π D.32π
9、如图,已知正方形的面积是36cm2,圆的面积是( )
A.9πcm2 B.18πcm2 C.36πcm2
10、一个圆形水池周长是31.4米,在它周围修一条1米宽的水泥路,水泥路面积是( )平方米.
A.34.54 B.65.94 C.3.14
二、填一填。
(1)如果圆的半径扩大到原来的2倍,那么直径扩大到原来的( )倍,周长扩大到原来的( )倍,面积扩大到原来的( )倍。
(2)如果一个环形的外圆半径用R表示,小圆半径用r表示,则圆环的面积
S=( )
(3)在一个长6厘米,宽4厘米的长方形内画一个最大的圆,这个圆的面积是( )平方厘米.
(4)图中大圆的半径是小圆的直径,大圆的面积是小圆的( )倍?
(5)两个圆的周长相等,这两个圆的面积( )
三、判断题。
(1)半圆的周长等于圆的周长的 。 ( )
(2)圆的直径缩小到原来的 ,面积也缩小到原来的 。 ( )
(3)圆环的面积等于外圆直径平方的π倍减去内圆直径平方的π倍。 ( )
(4)任何圆的圆周率都是π。 ( )
(5)两个圆的面积相等,则两个圆的半径一定相等。 ( )
四、求图形中阴影部分的面积。(单位:cm)
五、解决问题。
1、在一个直径是16米的圆心花坛周围,有一条宽为2米的小路围绕,小路的面积是多少平方米?
2、一个水缸,从里面量,缸口直径是 50厘米,缸壁厚 5厘米。要制做一个缸盖,使它正好盖住缸口的外沿,这个缸盖的面积是多少平方厘米?如果在缸盖的边沿贴上一圈金属(不计接头),这个金属条长多少厘米
3、在一张长为3米,宽为2米的长方形铁板上切割出一个最大的圆,剩下的面积是多少平方米?
4、碾是劳动人民智慧的结晶之一,在漫长的历史长河中起着巨大的作用。图中的这台碾安置在长为8米,宽为5米的房间里,碾台半径是0.8米,碾杆超出碾台1米,这个房间的安全区域(碾杆转一圈扫过的面积以外的部分)是多少平方米?
六、拓展提升。
我国古代有“天圆如张盖,地方如棋局”的说法。虽然这种说法是错误的,却产生了深远的影响,尤其体现在建筑设计上。下图是在中国建筑中经常见到的“外方内圆”和“外圆内方”的设计。假如这两个圆的半径都是0.8米,你知道哪个图形中正方形和圆之间部分的面积会大一些吗?
参考答案
1、
【答案】B
【解析】设大圆的半径为R,小圆的直径为d,半径为r,由题意知:
R=d=2r,根据圆的面积公式,大圆面积=π=π=4π,小圆面积=π,
所以大圆的面积是小圆的4倍.
2、
【答案】C
【解析】 由C=2πr可知,周长扩大3倍,半径也扩大 3倍,而面积=π,因此面积就扩大9倍。
3、
【答案】B
【解析】长可剪:7÷2≈3(个),宽可剪:4÷2=2(个),因此,最多可剪:3×2=6(个)。
4、
【答案】B
【解析】增加后的半径为9厘米,π×9?-π×6?=45π(平分厘米)
5、
【答案】C
【解析】用半径为4的圆的面积减去半径为3的圆的面积即可。
6、
【答案】A
【解析】利用周长先求半径,r===1,所以面积=3.14×1=3.14m?。
7、
【答案】C
【解析】设圆的半径为r,则扩大4倍后的半径为4r,利用圆的面积公式分别求出原来和现在的面积,即可求得扩大的倍数.
8、
【答案】A
【解析】根据圆环的面积公式:圆环的面积=π(R?﹣r?),计算即可求解.
9、
【答案】A 【解析】因为6×6=36,所以这个正方形的边长是6厘米,则圆的直径就是6厘米,圆的面积S=πr2,据此代入公式即可答案.
10、
【答案】A
【解析】根据环形面积=外圆面积﹣内圆面积,首先根据圆的周长公式:c=2πr,已知圆形水池的周长是31.4米,求出水池的半径,水池的半径加上1米就是外圆的半径,把数据代入环形面积公式S=π(R2﹣r2)答案即可.
水池的半径:
31.4÷3.14÷2=5(米),
水泥路的面积:
3.14×[(5+1)2﹣52]
=3.14×[36﹣25]
=3.14×11
=34.54(平方米).
二、填一填。
(1)
【答案】2、2、4
【解析】d=2r,周长=2d,面积=π,利用它们之间的关系即可解答。
(2)
【答案】π(R-r)
【解析】外圆面积减去小圆面积即可。
(3)
【答案】12.56
【解析】长方形内最大的圆的直径等于长方形的最短边4厘米,据此利用圆的面积公式计算即可.3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
(4)
【答案】4
【解析】大圆的半径等于小圆直径,即大圆的半径是小圆的半径的2倍;设小圆的半径为r,则大圆的半径就是2r,利用圆的面积公式即可分别求得大小圆的面积的倍数关系.
【答案】C
(5)
【解析】根据圆的周长公式可知两个圆的周长相等,则两个圆的半径相等,再根据圆的面积公式可知两个圆的半径相等,两个圆的面积就相等,再作出选择即可.
三、判断题。
(1)
【答案】错误
【解析】半圆的周长=圆的周长的一半+直径
(2)
【答案】错误
【解析】直径缩小到原来的,半径也缩小到原来的,则面积就缩小到原来的
(3)
【答案】错误
【解析】圆环的面积=π(R-r)
4)
【答案】正确
【解析】π是圆的周长与直径的比,是一个定值。
(5)
【答案】正确
【解析】圆面积=π,由于π是定值,面积相等,r一定相等。
四、求图形中阴影部分的面积。(单位:cm)
【答案】3.44;3.44;6.28;18.24
【解析】(1)4×4-3.14×2
=3.44(cm)
(2)4×4-3.14×2
=3.44(cm)
(3)×3.14×2
=6.28(cm)
(4)3.14×4-(×8×4)×2
=18.24(cm)
五、解决问题。
1、
【答案】3.14×(10-8)
=113.04(平方米)
【解析】外圆半径是:10米,内圆半径是:8米
小路面积是:3.14×(10-8)=113.04(平方米)
2、
【答案】3.14×30=2826(平方厘米);2×3.14×30=188.4(厘米)
【解析】(1)缸口外面的半径是30厘米
缸盖的面积是:3.14×30=2826(平方厘米)
(2)利用周长公式计算即可。
3、
【答案】2×3-3.14×1
=2.86(平方米)
【解析】由于长方形的宽为2米,所以最大圆的半径只能为1,剩下的面积=长方形的面积-圆的面积。
4、
【答案】5×8-3.14×(1+0.8)
=29.8264(平方米)
【解析】用房间的面积减去碾杆扫过的区域的面积就是安全区域的面积。
六、拓展提升。
【答案】第2个图形
【解析】
图(1) 图(2)
要想知道哪个图形中正方形和圆之间部分的面积会大一些,首先要求出每个图
形中正方形和圆之间部分的面积,然后再比大小。
从图(1)可以看出:正方形的面积是:1.6×1.6=2.56(m)
圆的面积是:3.14×0.8=2.0096(m),则正方形和圆之间部分的面积是:
2.56-2.0096=0.5504(m)
从图(2)可以看出:圆的面积是:3.14×0.8=2.0096(m),正方形的面积是:(×0.8×0.8)×4=1.28(m)则正方形和圆之间部分的面积是:2.0096-1.28=0.7296(m)。因为0.5504<0.7296,所以第2个图形中正方形和圆之间部分的面积要大一些。
