五年级上册数学单元测试-6.多边形面积 冀教版(含答案)
文档属性
| 名称 | 五年级上册数学单元测试-6.多边形面积 冀教版(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 134.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-25 00:00:00 | ||
图片预览




文档简介
五年级上册数学单元测试-6.多边形面积
一、单选题
1.一个平行四边形的面积是8平方厘米,和它等底等高的三角形的面积是???? 平方厘米.
A.?16?????????????????????????????????????????????B.?8?????????????????????????????????????????????C.?4
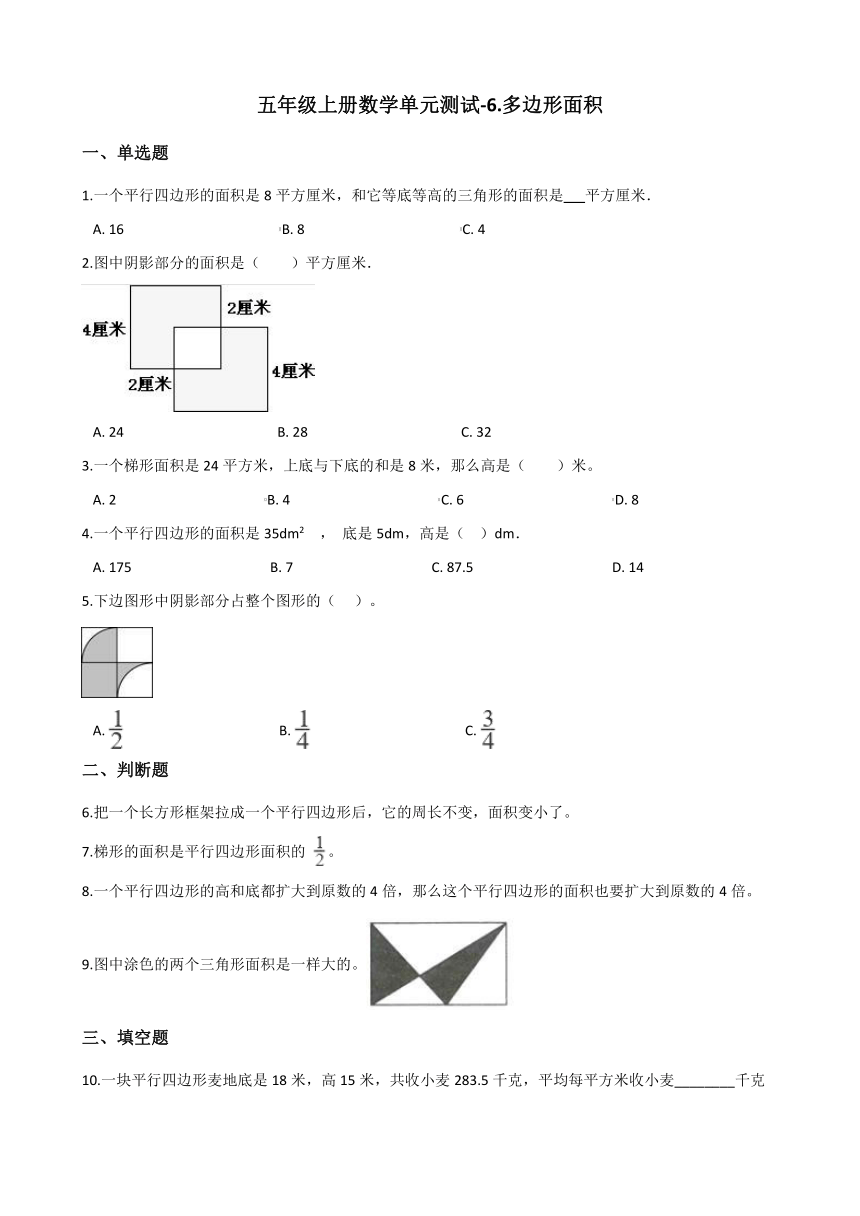
2.图中阴影部分的面积是( )平方厘米.
A.?24????????????????????????????????????????????B.?28????????????????????????????????????????????C.?32
3.一个梯形面积是24平方米,上底与下底的和是8米,那么高是( )米。
A.?2???????????????????????????????????????????B.?4???????????????????????????????????????????C.?6???????????????????????????????????????????D.?8
4.一个平行四边形的面积是35dm2 , 底是5dm,高是(?? )dm.
A.?175????????????????????????????????????????B.?7????????????????????????????????????????C.?87.5????????????????????????????????????????D.?14
5.下边图形中阴影部分占整个图形的(??? )。
A.?????????????????????????????????????????????B.?????????????????????????????????????????????C.?
二、判断题
6.把一个长方形框架拉成一个平行四边形后,它的周长不变,面积变小了。
7.梯形的面积是平行四边形面积的 。
8.一个平行四边形的高和底都扩大到原数的4倍,那么这个平行四边形的面积也要扩大到原数的4倍。
9.图中涂色的两个三角形面积是一样大的。
三、填空题
10.一块平行四边形麦地底是18米,高15米,共收小麦283.5千克,平均每平方米收小麦________千克
11.选择合适条件,计算下面图形(单位:厘米)的面积是________
12.一个平行四边形的面积是72 cm2 , 底是18 cm,高是________?cm。
13.估一估,下面每个图形所占的面积大约是多少?(每个小方格的面积表示1cm2)________
14.一个平行四边形相邻的两条边长分别是8厘米和4厘米,其中一条边上的高是6厘米.这个平行四边形的面积是________平方厘米
四、解答题
15.计算图形的面积
16.已知一个梯形的面积是58平方厘米,它的上底是15厘米,下底是25厘米,它的高是多少厘米?
五、综合题
17.写出下面各图形的面积.(假设1格为1平方厘米)
(1)图①面积是________平方厘米。
(2)图②面积是________平方厘米。
(3)图③面积是________平方厘米。
六、应用题
18.幸福乡挖一条水渠的横截面是梯形,渠口宽2.8米,渠底宽1.4米,渠深1.2米,如下图所示,它的横截面的面积是多少平方米?
19.如图是一种机械零件的剖面图,求这种零件剖面的面积.(单位:厘米)
参考答案
一、单选题
1.【答案】 C
【解析】【解答】8÷2=4(平方厘米)
故答案为:C
【分析】平行四边形面积=底×高,三角形面积=底×高÷2,等底等高的三角形面积是平行四边形面积的一半.
2.【答案】A
【解析】【解答】解:4×4×2﹣2×2×2
=32﹣8
=24(平方厘米)
答:阴影部分的面积是24平方厘米.
故选:A.
【分析】阴影部分的面积就等于两个大正方形的面积减去两个小正方形的面积,据此解答即可.
3.【答案】 C
【解析】【解答】24×2÷8
=48÷8
=6(米)
所以,这个梯形的高是6米。
【分析】根据梯形的面积公式可得:梯形的高=梯形的面积×2÷上下底之和,据此代入数据即可解答,关键是掌握梯形面积公式的灵活应用。
4.【答案】 B
【解析】【解答】解:这个平行四边形的高是35÷5=7dm。 故答案为:B。 【分析】平行四边形的面积=底×高,据此作答即可。
5.【答案】 A
【解析】【解答】将两个扇形区域的阴影图形拼合在一起,就组成了一个小正方形,阴影共有2个小正方形,所以占整个图形的. 故答案为:A. 【分析】运用图形的拼合,转化成小正方形进行计算,也可以假设小正方形的边长为1,计算阴影面积.
二、判断题
6.【答案】正确
【解析】【解答】把一个长方形框架拉成一个平行四边形后,它的周长不变,面积变小了,原题说法正确. 故答案为:正确.【分析】要比较平行四边形和长方形有没有变化,则要先看看它们的高和底有没有变化,由题意可知:长方形被拉成平行四边形后,底的大小没变,而高变小了,据此可得出结论:把长方形拉成平行四边形,四条边的长度没变,则其周长不变;但是它的高变短了,所以它的面积就变小了,据此判断.
7.【答案】错误
【解析】【解答】解:因为平行四边形的面积=底×高,梯形的面积=(上底+下底)×高÷2, 如果不知道平行四边形的底和高与梯形的底和高的大小关系, 则不能判断它们的面积的大小. 所以说“梯形的面积是平行四边形面积的 ”是错误的. 故答案为:错误. 【分析】平行四边形的面积=底×高,梯形的面积=(上底+下底)×高÷2,等底等高的梯形的面积是平行四边形的面积的 ,如果不知道平行四边形的底和高与梯形的底和高的大小关系,则不能判断它们的面积的大小.解答此题的关键是:依据平行四边形和梯形的面积公式即可作答.
8.【答案】错误
【解析】【解答】解:4×4=16,一个平行四边形的高和底都扩大到原数的4倍,那么这个平行四边形的面积要扩大到原来的16倍。原题说法错误。 故答案为:错误
【分析】平行四边形面积=底×高,平行四边形面积扩大的倍数是底和高扩大的倍数的乘积。
9.【答案】正确
【解析】【解答】解:图中涂色的两个三角形面积都是等底等高的两个三角形面积减去两个三角形重叠部分的面积,两部分面积是相等的。 故答案为:正确【分析】两个三角形的面积都可以看做是等底等高的两个三角形面积减去重叠部分的面积,等底等高的两个三角形面积相等,所以这两个涂色三角形的面积也相等。
三、填空题
10.【答案】1.05
【解析】【解答】解:283.5÷(18×15) =283.5÷270 =1.05(千克) 答:平均每平方米收小麦1.05千克
11.【答案】240平方厘米
【解析】【解答】15×16=240(平方厘米) 故答案为:240平方厘米 【分析】平行四边形的面积=底×高,由此根据公式计算即可.
12.【答案】4
【解析】【解答】解:72÷18=4(cm) 故答案为:4【分析】平行四边形面积=底×高,用平行四边形面积除以底即可求出高。
13.【答案】28cm2;30cm2;28cm2
【解析】【解答】解:第一个图形,整格的23个,是23平方厘米,半格的约有10个,是5平方厘米,总面积是28平方厘米; 第二个图形,整格的23个,是23平方厘米,半格的14个,约有7平方厘米,总面积是30平方厘米; 第三个图形,整格的是24格,是24平方厘米,半格的8个,约有4平方厘米,总面积是28平方厘米。 故答案为:28cm2;30cm2;28cm2【分析】先数出整格的有多少个,再数出半格的有多少个,把两个半格的看作一个整格的来估算面积即可。
14.【答案】24
【解析】【解答】解:6×4=24(平方厘米) 故答案为:24. 【分析】本题考查的主要内容是平行四边形的面积的应用问题,根据平行四边形的面积公式进行分析即可.
四、解答题
15.【答案】解:可分割成一个梯形和一个长方形,如图所示: (17+20)×(15-9)÷2 =37×6÷2 =222÷2 =111(cm2) 111+20×9 =111+180 =291(cm2) 答:图形的面积是291cm2.
【解析】【分析】观察图可知,可以将此图分割成一个梯形和一个长方形,梯形的上底是17cm,下底是20cm,高是15-9=6cm,长方形的长是20cm,宽是9cm,然后用梯形的面积+长方形的面积=组合图形的面积,据此列式解答.
16.【答案】解:58×2÷(15+25) =116÷40 =2.9(厘米), 答:它的高是2.9厘米
【解析】【分析】根据梯形的面积公式:s=(a+b)×h÷2,那么h=2s÷(a+b),据此解答.此题主要考查梯形面积公式的灵活运用,关键是熟记公式.
五、综合题
17.【答案】(1)12 (2)10 (3)15
【解析】【解答】解:(1)整格的6个,半格的12个,工12平方厘米; (2)整格的2个,半格的16个,共10平方厘米; (3)整格的11个,半格的8个,工15平方厘米. 故答案为:12;10;15
【分析】可以采用数方格的方法,先数出整格的,再数出不是整格的,把两个不是整格的合成一个整格的来判断总面积即可.
六、应用题
18.【答案】解: S=(a+b)·h÷2 =(2.8+1.4)×1.2÷2 =4.2×1.2÷2 =2.52(平方米)。 答:它的横截面的面积是2.52平方米。
【解析】【分析】求梯形的面积时,一定要先把上底、下底和高一一对应好,根据公式来计算,而且千万不要忘记“除以2”。 要熟记梯形的面积公式,才能才能解决实际问题。 这是一道直接应用公式进行计算的题。渠口宽相当于梯形的上底,渠底宽相当于梯形的下底,渠深相当于梯形的高,应用梯形的面积公式S=(a+b)·h÷2即可求解。
19.【答案】解:5×3+3×2÷2=15+3 =18(平方厘米) 答:这个零件的剖面图的面积是18平方厘米.
【解析】【分析】剖面的面积是长方形面积加上三角形面积,长方形面积=长×宽,三角形面积=底×高÷2,根据面积公式计算即可.
一、单选题
1.一个平行四边形的面积是8平方厘米,和它等底等高的三角形的面积是???? 平方厘米.
A.?16?????????????????????????????????????????????B.?8?????????????????????????????????????????????C.?4
2.图中阴影部分的面积是( )平方厘米.
A.?24????????????????????????????????????????????B.?28????????????????????????????????????????????C.?32
3.一个梯形面积是24平方米,上底与下底的和是8米,那么高是( )米。
A.?2???????????????????????????????????????????B.?4???????????????????????????????????????????C.?6???????????????????????????????????????????D.?8
4.一个平行四边形的面积是35dm2 , 底是5dm,高是(?? )dm.
A.?175????????????????????????????????????????B.?7????????????????????????????????????????C.?87.5????????????????????????????????????????D.?14
5.下边图形中阴影部分占整个图形的(??? )。
A.?????????????????????????????????????????????B.?????????????????????????????????????????????C.?
二、判断题
6.把一个长方形框架拉成一个平行四边形后,它的周长不变,面积变小了。
7.梯形的面积是平行四边形面积的 。
8.一个平行四边形的高和底都扩大到原数的4倍,那么这个平行四边形的面积也要扩大到原数的4倍。
9.图中涂色的两个三角形面积是一样大的。
三、填空题
10.一块平行四边形麦地底是18米,高15米,共收小麦283.5千克,平均每平方米收小麦________千克
11.选择合适条件,计算下面图形(单位:厘米)的面积是________
12.一个平行四边形的面积是72 cm2 , 底是18 cm,高是________?cm。
13.估一估,下面每个图形所占的面积大约是多少?(每个小方格的面积表示1cm2)________
14.一个平行四边形相邻的两条边长分别是8厘米和4厘米,其中一条边上的高是6厘米.这个平行四边形的面积是________平方厘米
四、解答题
15.计算图形的面积
16.已知一个梯形的面积是58平方厘米,它的上底是15厘米,下底是25厘米,它的高是多少厘米?
五、综合题
17.写出下面各图形的面积.(假设1格为1平方厘米)
(1)图①面积是________平方厘米。
(2)图②面积是________平方厘米。
(3)图③面积是________平方厘米。
六、应用题
18.幸福乡挖一条水渠的横截面是梯形,渠口宽2.8米,渠底宽1.4米,渠深1.2米,如下图所示,它的横截面的面积是多少平方米?
19.如图是一种机械零件的剖面图,求这种零件剖面的面积.(单位:厘米)
参考答案
一、单选题
1.【答案】 C
【解析】【解答】8÷2=4(平方厘米)
故答案为:C
【分析】平行四边形面积=底×高,三角形面积=底×高÷2,等底等高的三角形面积是平行四边形面积的一半.
2.【答案】A
【解析】【解答】解:4×4×2﹣2×2×2
=32﹣8
=24(平方厘米)
答:阴影部分的面积是24平方厘米.
故选:A.
【分析】阴影部分的面积就等于两个大正方形的面积减去两个小正方形的面积,据此解答即可.
3.【答案】 C
【解析】【解答】24×2÷8
=48÷8
=6(米)
所以,这个梯形的高是6米。
【分析】根据梯形的面积公式可得:梯形的高=梯形的面积×2÷上下底之和,据此代入数据即可解答,关键是掌握梯形面积公式的灵活应用。
4.【答案】 B
【解析】【解答】解:这个平行四边形的高是35÷5=7dm。 故答案为:B。 【分析】平行四边形的面积=底×高,据此作答即可。
5.【答案】 A
【解析】【解答】将两个扇形区域的阴影图形拼合在一起,就组成了一个小正方形,阴影共有2个小正方形,所以占整个图形的. 故答案为:A. 【分析】运用图形的拼合,转化成小正方形进行计算,也可以假设小正方形的边长为1,计算阴影面积.
二、判断题
6.【答案】正确
【解析】【解答】把一个长方形框架拉成一个平行四边形后,它的周长不变,面积变小了,原题说法正确. 故答案为:正确.【分析】要比较平行四边形和长方形有没有变化,则要先看看它们的高和底有没有变化,由题意可知:长方形被拉成平行四边形后,底的大小没变,而高变小了,据此可得出结论:把长方形拉成平行四边形,四条边的长度没变,则其周长不变;但是它的高变短了,所以它的面积就变小了,据此判断.
7.【答案】错误
【解析】【解答】解:因为平行四边形的面积=底×高,梯形的面积=(上底+下底)×高÷2, 如果不知道平行四边形的底和高与梯形的底和高的大小关系, 则不能判断它们的面积的大小. 所以说“梯形的面积是平行四边形面积的 ”是错误的. 故答案为:错误. 【分析】平行四边形的面积=底×高,梯形的面积=(上底+下底)×高÷2,等底等高的梯形的面积是平行四边形的面积的 ,如果不知道平行四边形的底和高与梯形的底和高的大小关系,则不能判断它们的面积的大小.解答此题的关键是:依据平行四边形和梯形的面积公式即可作答.
8.【答案】错误
【解析】【解答】解:4×4=16,一个平行四边形的高和底都扩大到原数的4倍,那么这个平行四边形的面积要扩大到原来的16倍。原题说法错误。 故答案为:错误
【分析】平行四边形面积=底×高,平行四边形面积扩大的倍数是底和高扩大的倍数的乘积。
9.【答案】正确
【解析】【解答】解:图中涂色的两个三角形面积都是等底等高的两个三角形面积减去两个三角形重叠部分的面积,两部分面积是相等的。 故答案为:正确【分析】两个三角形的面积都可以看做是等底等高的两个三角形面积减去重叠部分的面积,等底等高的两个三角形面积相等,所以这两个涂色三角形的面积也相等。
三、填空题
10.【答案】1.05
【解析】【解答】解:283.5÷(18×15) =283.5÷270 =1.05(千克) 答:平均每平方米收小麦1.05千克
11.【答案】240平方厘米
【解析】【解答】15×16=240(平方厘米) 故答案为:240平方厘米 【分析】平行四边形的面积=底×高,由此根据公式计算即可.
12.【答案】4
【解析】【解答】解:72÷18=4(cm) 故答案为:4【分析】平行四边形面积=底×高,用平行四边形面积除以底即可求出高。
13.【答案】28cm2;30cm2;28cm2
【解析】【解答】解:第一个图形,整格的23个,是23平方厘米,半格的约有10个,是5平方厘米,总面积是28平方厘米; 第二个图形,整格的23个,是23平方厘米,半格的14个,约有7平方厘米,总面积是30平方厘米; 第三个图形,整格的是24格,是24平方厘米,半格的8个,约有4平方厘米,总面积是28平方厘米。 故答案为:28cm2;30cm2;28cm2【分析】先数出整格的有多少个,再数出半格的有多少个,把两个半格的看作一个整格的来估算面积即可。
14.【答案】24
【解析】【解答】解:6×4=24(平方厘米) 故答案为:24. 【分析】本题考查的主要内容是平行四边形的面积的应用问题,根据平行四边形的面积公式进行分析即可.
四、解答题
15.【答案】解:可分割成一个梯形和一个长方形,如图所示: (17+20)×(15-9)÷2 =37×6÷2 =222÷2 =111(cm2) 111+20×9 =111+180 =291(cm2) 答:图形的面积是291cm2.
【解析】【分析】观察图可知,可以将此图分割成一个梯形和一个长方形,梯形的上底是17cm,下底是20cm,高是15-9=6cm,长方形的长是20cm,宽是9cm,然后用梯形的面积+长方形的面积=组合图形的面积,据此列式解答.
16.【答案】解:58×2÷(15+25) =116÷40 =2.9(厘米), 答:它的高是2.9厘米
【解析】【分析】根据梯形的面积公式:s=(a+b)×h÷2,那么h=2s÷(a+b),据此解答.此题主要考查梯形面积公式的灵活运用,关键是熟记公式.
五、综合题
17.【答案】(1)12 (2)10 (3)15
【解析】【解答】解:(1)整格的6个,半格的12个,工12平方厘米; (2)整格的2个,半格的16个,共10平方厘米; (3)整格的11个,半格的8个,工15平方厘米. 故答案为:12;10;15
【分析】可以采用数方格的方法,先数出整格的,再数出不是整格的,把两个不是整格的合成一个整格的来判断总面积即可.
六、应用题
18.【答案】解: S=(a+b)·h÷2 =(2.8+1.4)×1.2÷2 =4.2×1.2÷2 =2.52(平方米)。 答:它的横截面的面积是2.52平方米。
【解析】【分析】求梯形的面积时,一定要先把上底、下底和高一一对应好,根据公式来计算,而且千万不要忘记“除以2”。 要熟记梯形的面积公式,才能才能解决实际问题。 这是一道直接应用公式进行计算的题。渠口宽相当于梯形的上底,渠底宽相当于梯形的下底,渠深相当于梯形的高,应用梯形的面积公式S=(a+b)·h÷2即可求解。
19.【答案】解:5×3+3×2÷2=15+3 =18(平方厘米) 答:这个零件的剖面图的面积是18平方厘米.
【解析】【分析】剖面的面积是长方形面积加上三角形面积,长方形面积=长×宽,三角形面积=底×高÷2,根据面积公式计算即可.
