人教A版高中数学必修二 课件 2.1.1 空间点、直线、平面之间的位置关系 :30张PPT
文档属性
| 名称 | 人教A版高中数学必修二 课件 2.1.1 空间点、直线、平面之间的位置关系 :30张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 21:44:53 | ||
图片预览









文档简介
课件30张PPT。第二章 点、直线、平面之间的位置关系
2.1 空间点、直线、平面之间的位置关系
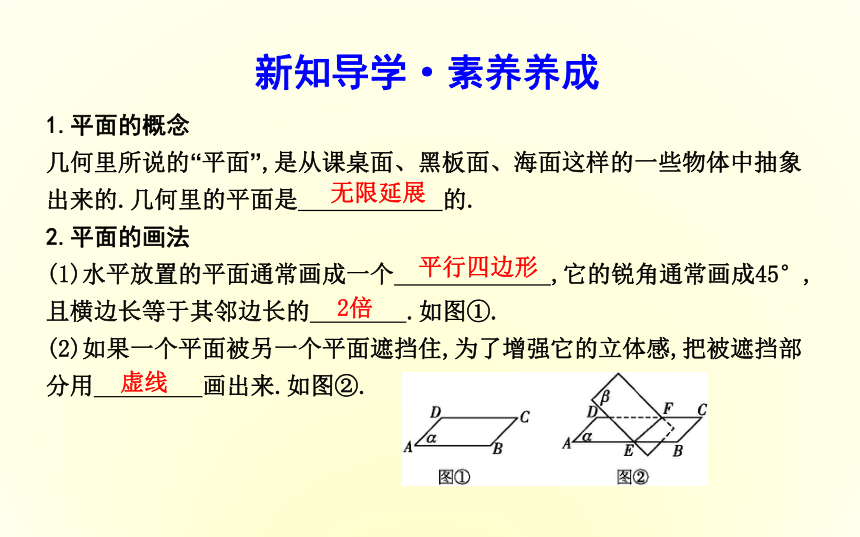
2.1.1 平 面目标导航新知导学·素养养成1.平面的概念
几何里所说的“平面”,是从课桌面、黑板面、海面这样的一些物体中抽象出来的.几何里的平面是 的.
2.平面的画法
(1)水平放置的平面通常画成一个 ,它的锐角通常画成45°,且横边长等于其邻边长的 .如图①.
(2)如果一个平面被另一个平面遮挡住,为了增强它的立体感,把被遮挡部分用 画出来.如图②.无限延展平行四边形2倍虚线3.平面的表示法
图①的平面可表示为 、平面ABCD、平面AC或平面BD.
4.点、线、面之间的关系
(1)直线在平面内的概念:
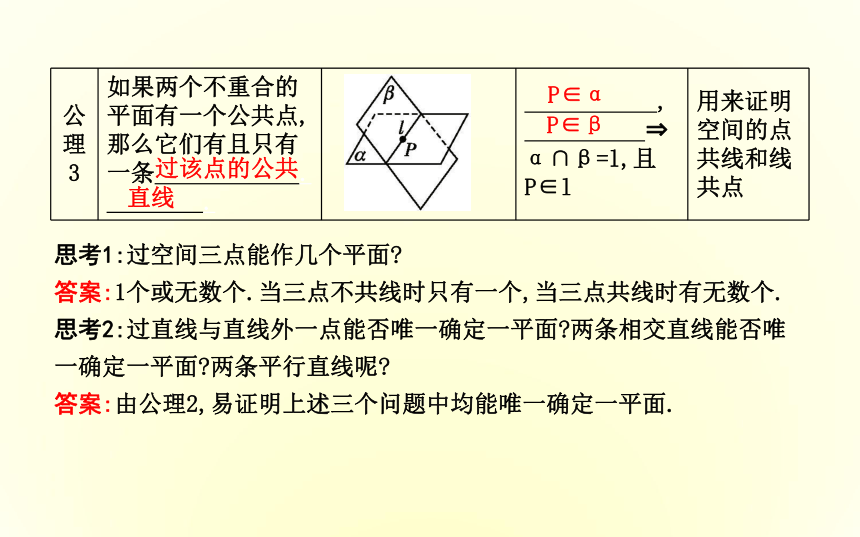
如果直线l上的 都在平面α内,就说直线l在平面α内,或者说平面α经过直线l.平面α所有点(2)一些文字语言与数学符号的对应关系:A∈lA?lA∈αA?αl?αl?α5.平面的基本性质两点A∈l B∈lA∈α B∈α不在一条直 线上过该点的公共直线思考1:过空间三点能作几个平面?
答案:1个或无数个.当三点不共线时只有一个,当三点共线时有无数个.
思考2:过直线与直线外一点能否唯一确定一平面?两条相交直线能否唯一确定一平面?两条平行直线呢?
答案:由公理2,易证明上述三个问题中均能唯一确定一平面.P∈α P∈β名师点津(1)平面和点、直线一样,是只描述而不加定义的原始概念,不能进行
度量;
(2)平面无厚薄、无大小,是无限延展的.课堂探究·素养提升题型一 文字语言、图形语言、符号语言的转换
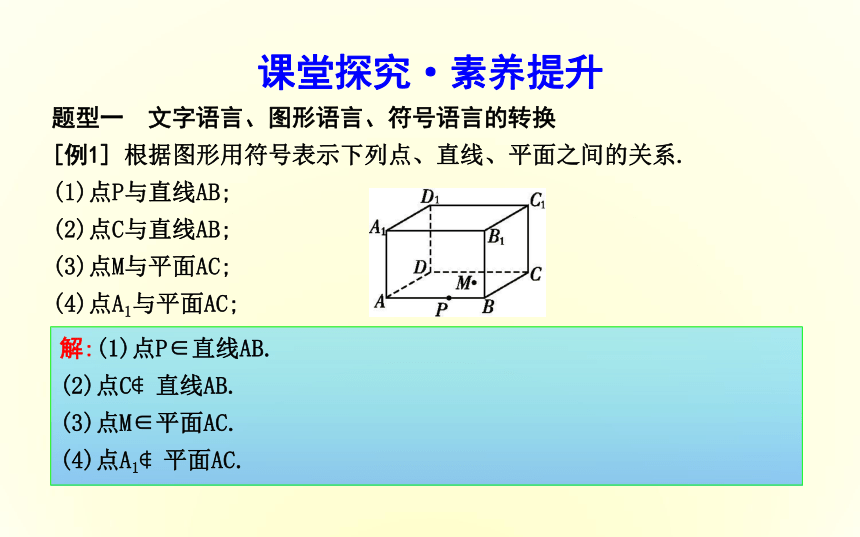
[例1] 根据图形用符号表示下列点、直线、平面之间的关系.
(1)点P与直线AB;
(2)点C与直线AB;
(3)点M与平面AC;
(4)点A1与平面AC;解:(1)点P∈直线AB.
(2)点C?直线AB.
(3)点M∈平面AC.
(4)点A1?平面AC.解:(5)直线AB∩直线BC=点B.
(6)直线AB?平面AC.
(7)平面A1B∩平面AC=直线AB.(5)直线AB与直线BC;
(6)直线AB与平面AC;
(7)平面A1B与平面AC.方法技巧(1)用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.
(2)要注意符号语言的意义.如点与直线的位置关系只能用“∈”或“?”表示,直线与平面的位置关系只能用“?”或“?”表示.
(3)由符号语言或文字语言画相应的图形时,要注意实线和虚线的
区别.即时训练1-1:根据下列符号表示的语句,说明点、线、面之间的位置关系,并画出相应的图形:
(1)A∈α,B?α;
(2)l?α,m∩α=A,A?l;
(3)P∈l,P?α,Q∈l,Q∈α.解:(1)点A在平面α内,点B不在平面α内;
(2)直线l在平面α内,直线m与平面α相交于点A,且点A不在直线l上;
(3)直线l经过平面α外一点P和平面α内一点Q.
图形分别如图(1),(2),(3)所示.[备用例1]
1.如图,用符号语言表示下列图形中点、直线、平面之间的位置关系.解:在(1)中,α∩β=l,a∩α=A,a∩β=B.
在(2)中,α∩β=l,a?α,b?β,a∩l=P,b∩l=P.2.根据下列条件,画出图形.
(1)平面α∩平面β=l,直线AB?α,AB∥l,E∈AB,直线EF∩β=F,F?l;
(2)平面α∩平面β=a,△ABC的三个顶点满足条件:A∈a,B∈α,B?a, C∈β,C?a.答案:如图题型二 点线共面
[例2] 证明:两两相交且不过同一点的三条直线在同一平面内.证明:法一(纳入法)
因为l1∩l2=A,
所以l1和l2确定一个平面α.
因为l2∩l3=B,
所以B∈l2.又因为l2?α,
所以B∈α.
同理可证C∈α.
又因为B∈l3,C∈l3,所以l3?α.
所以直线l1,l2,l3在同一平面内.法二 (重合法)
因为l1∩l2=A,
所以l1,l2确定一个平面α.
因为l2∩l3=B,
所以l2,l3确定一个平面β.
因为A∈l2,l2?α,所以A∈α.
因为A∈l2,l2?β,所以A∈β.
同理可证B∈α,B∈β,C∈α,C∈β.
所以不共线的三个点A,B,C既在平面α内,又在平面β内.
所以平面α和β重合,即直线l1,l2,l3在同一平面内.方法技巧在证明多线共面时,可用下面的两种方法来证明:
(1)纳入法:先由部分直线确定一个平面,再证明其他直线在这个平
面内.
(2)重合法:即先证明一些元素在一个平面内,再证明另一些元素在另一个平面内,然后证明这两个平面重合,即证得所有元素在同一个平面内.即时训练2-1:已知直线a∥b,直线l与a,b都相交,求证:过a,b,l有且只有一个平面.证明:如图所示.
由已知a∥b,所以过a,b有且只有一个平面α.
设a∩l=A,b∩l=B,
所以A∈α,B∈α,且A∈l,B∈l,
所以l?α.
即过a,b,l有且只有一个平面.[备用例2]
1.如图,已知直线a∥b∥c,l∩a=A,l∩b=B,l∩c=C.求证:a,b,c,l共面.证明:因为a∥b,
所以a,b确定一个平面α.
因为l∩a=A,l∩b=B,
所以A∈α,B∈α.又因为A∈l,B∈l,
所以l?α.因为b∥c,
所以b,c确定一个平面β.
同理可证l?β.于是b?α,l?α,b?β,l?β,
即α∩β=b,α∩β=l.
又因为b与l不重合,所以α与β重合,所以a,b,c,l共面.2.已知四条直线两两相交,且不共点,求证:这四条直线在同一平面内.已知:a,b,c,d四条直线两两相交,且不共点,
求证:a,b,c,d四线共面.
证明:(1)若a,b,c三线共点于O,
如图所示,因为O?d,
所以经过d与点O有且只有一个平面α.
因为A,B,C分别是d与a,b,c的交点,
所以A,B,C三点在平面α内.
由公理1知a,b,c都在平面α内,
故a,b,c,d共面.(2)若a,b,c,d无三线共点,如图所示,
因为a∩b=A,
所以经过a,b有且仅有一个平面α,
所以B,C∈α.
由公理1知c?α.
同理,d?α,从而有a,b,c,d共面.
综上所述,四条直线两两相交,且不共点,这四条直线在同一平面内.题型三 多点共线、多线共点问题
[例3] (12分)如图,在正方体ABCD-A1B1C1D1中,点M,N,E,F分别是棱CD,AB, DD1,AA1上的点,若MN与EF交于点Q,求证:D,A,Q三点共线.规范解答:因为MN∩EF=Q,
所以Q∈直线MN,Q∈直线EF,……………………2分
又因为M∈直线CD,N∈直线AB,
CD?平面ABCD,AB?平面ABCD.
所以M,N∈平面ABCD,………………………………5分
所以MN?平面ABCD.
所以Q∈平面ABCD.………………………………7分
同理,可得EF?平面ADD1A1.
所以Q∈平面ADD1A1,………………………………9分
又因为平面ABCD∩平面ADD1A1=AD,
所以Q∈直线AD,
即D,A,Q三点共线.………………………………12分一题多变:本例中,若设线段A1C与平面ABC1D1交于点Q,求证:B,Q,D1三点
共线.证明:如图,连接A1B,CD1,显然B∈平面A1BCD1,
D1∈平面A1BCD1.所以BD1?平面A1BCD1.
同理BD1?平面ABC1D1.
所以平面ABC1D1∩平面A1BCD1=BD1.
因为A1C∩平面ABC1D1=Q,
所以Q∈平面ABC1D1.
又因为A1C?平面A1BCD1,
所以Q∈平面A1BCD1.
所以Q在平面A1BCD1与ABC1D1的交线上,
即Q∈BD1,所以B,Q,D1三点共线.方法技巧点共线与线共点的证明方法:
(1)点共线:证明多点共线通常利用公理3,即两相交平面交线的唯一性,通过证明点分别在两个平面内,证明点在相交平面的交线上,也可选择其中两点确定一条直线,然后证明其他点也在其上.
(2)三线共点:证明三线共点问题可把其中一条作为分别过其余两条直线的两个平面的交线,然后再证两条直线的交点在此直线上,此外还可先将其中一条直线看作某两个平面的交线,证明该交线与另两条直线分别交于两点,再证点重合,从而得三线共点.[备用例3]
三个平面两两相交于三条直线,若这三条直线不平行,求证:这三条直线交于一点.已知平面α,β,γ两两相交于三条直线l1,l2,l3,且l1,l2,l3不平行.
求证:l1,l2,l3相交于一点.
证明:如图,α∩β=l1,β∩γ=l2,α∩γ=l3,
因为l1?β,l2?β,且l1,l2不平行,
所以l1与l2必相交.
设l1∩l2=P,则P∈l1?α,P∈l2?γ,
所以P∈α∩γ=l3.
所以l1,l2,l3相交于一点.课堂达标解析:几何中的平面是无限延展的,不可进行所有类型的度量,容易判断所有命题都不对.1.下列命题中正确的个数是( )
①一个平面长4米,宽2米;
②2个平面重叠在一起比一个平面厚;
③一个平面的面积是25平方米;
④将一个平面内的一条直线延长,它就会伸出这个平面.
(A)0 (B)1 (C)2 (D)3A解析:A.不是公理,是个常用的结论,需经过推理论证;B,C,D都是平面的基本性质公理.2.在下列命题中,不是公理的是( )
(A)平行于同一个平面的两个平面相互平行
(B)过不在同一条直线上的三点,有且只有一个平面
(C)如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内
(D)如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线A解析:因为A∈α,A∈β,所以A∈α∩β.
由公理可知α∩β为经过A的一条直线而不是A.
故α∩β=A错误.3.已知α,β为平面,A,B,M,N为点,a为直线,下列推理错误的是( )
(A)A∈a,A∈β,B∈a,B∈β?a?β
(B)M∈α,M∈β,N∈α,N∈β?α∩β=MN
(C)A∈α,A∈β?α∩β=A
(D)A,B,M∈α,A,B,M∈β,且A,B,M不共线?α,β重合C4.设平面α与平面β交于直线l,A∈α,B∈α,且直线AB∩l=C,则直线AB∩β= .?解析:因为α∩β=l,AB∩l=C,
所以C∈β,C∈AB,
所以AB∩β=C.
答案:C
2.1 空间点、直线、平面之间的位置关系
2.1.1 平 面目标导航新知导学·素养养成1.平面的概念
几何里所说的“平面”,是从课桌面、黑板面、海面这样的一些物体中抽象出来的.几何里的平面是 的.
2.平面的画法
(1)水平放置的平面通常画成一个 ,它的锐角通常画成45°,且横边长等于其邻边长的 .如图①.
(2)如果一个平面被另一个平面遮挡住,为了增强它的立体感,把被遮挡部分用 画出来.如图②.无限延展平行四边形2倍虚线3.平面的表示法
图①的平面可表示为 、平面ABCD、平面AC或平面BD.
4.点、线、面之间的关系
(1)直线在平面内的概念:
如果直线l上的 都在平面α内,就说直线l在平面α内,或者说平面α经过直线l.平面α所有点(2)一些文字语言与数学符号的对应关系:A∈lA?lA∈αA?αl?αl?α5.平面的基本性质两点A∈l B∈lA∈α B∈α不在一条直 线上过该点的公共直线思考1:过空间三点能作几个平面?
答案:1个或无数个.当三点不共线时只有一个,当三点共线时有无数个.
思考2:过直线与直线外一点能否唯一确定一平面?两条相交直线能否唯一确定一平面?两条平行直线呢?
答案:由公理2,易证明上述三个问题中均能唯一确定一平面.P∈α P∈β名师点津(1)平面和点、直线一样,是只描述而不加定义的原始概念,不能进行
度量;
(2)平面无厚薄、无大小,是无限延展的.课堂探究·素养提升题型一 文字语言、图形语言、符号语言的转换
[例1] 根据图形用符号表示下列点、直线、平面之间的关系.
(1)点P与直线AB;
(2)点C与直线AB;
(3)点M与平面AC;
(4)点A1与平面AC;解:(1)点P∈直线AB.
(2)点C?直线AB.
(3)点M∈平面AC.
(4)点A1?平面AC.解:(5)直线AB∩直线BC=点B.
(6)直线AB?平面AC.
(7)平面A1B∩平面AC=直线AB.(5)直线AB与直线BC;
(6)直线AB与平面AC;
(7)平面A1B与平面AC.方法技巧(1)用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.
(2)要注意符号语言的意义.如点与直线的位置关系只能用“∈”或“?”表示,直线与平面的位置关系只能用“?”或“?”表示.
(3)由符号语言或文字语言画相应的图形时,要注意实线和虚线的
区别.即时训练1-1:根据下列符号表示的语句,说明点、线、面之间的位置关系,并画出相应的图形:
(1)A∈α,B?α;
(2)l?α,m∩α=A,A?l;
(3)P∈l,P?α,Q∈l,Q∈α.解:(1)点A在平面α内,点B不在平面α内;
(2)直线l在平面α内,直线m与平面α相交于点A,且点A不在直线l上;
(3)直线l经过平面α外一点P和平面α内一点Q.
图形分别如图(1),(2),(3)所示.[备用例1]
1.如图,用符号语言表示下列图形中点、直线、平面之间的位置关系.解:在(1)中,α∩β=l,a∩α=A,a∩β=B.
在(2)中,α∩β=l,a?α,b?β,a∩l=P,b∩l=P.2.根据下列条件,画出图形.
(1)平面α∩平面β=l,直线AB?α,AB∥l,E∈AB,直线EF∩β=F,F?l;
(2)平面α∩平面β=a,△ABC的三个顶点满足条件:A∈a,B∈α,B?a, C∈β,C?a.答案:如图题型二 点线共面
[例2] 证明:两两相交且不过同一点的三条直线在同一平面内.证明:法一(纳入法)
因为l1∩l2=A,
所以l1和l2确定一个平面α.
因为l2∩l3=B,
所以B∈l2.又因为l2?α,
所以B∈α.
同理可证C∈α.
又因为B∈l3,C∈l3,所以l3?α.
所以直线l1,l2,l3在同一平面内.法二 (重合法)
因为l1∩l2=A,
所以l1,l2确定一个平面α.
因为l2∩l3=B,
所以l2,l3确定一个平面β.
因为A∈l2,l2?α,所以A∈α.
因为A∈l2,l2?β,所以A∈β.
同理可证B∈α,B∈β,C∈α,C∈β.
所以不共线的三个点A,B,C既在平面α内,又在平面β内.
所以平面α和β重合,即直线l1,l2,l3在同一平面内.方法技巧在证明多线共面时,可用下面的两种方法来证明:
(1)纳入法:先由部分直线确定一个平面,再证明其他直线在这个平
面内.
(2)重合法:即先证明一些元素在一个平面内,再证明另一些元素在另一个平面内,然后证明这两个平面重合,即证得所有元素在同一个平面内.即时训练2-1:已知直线a∥b,直线l与a,b都相交,求证:过a,b,l有且只有一个平面.证明:如图所示.
由已知a∥b,所以过a,b有且只有一个平面α.
设a∩l=A,b∩l=B,
所以A∈α,B∈α,且A∈l,B∈l,
所以l?α.
即过a,b,l有且只有一个平面.[备用例2]
1.如图,已知直线a∥b∥c,l∩a=A,l∩b=B,l∩c=C.求证:a,b,c,l共面.证明:因为a∥b,
所以a,b确定一个平面α.
因为l∩a=A,l∩b=B,
所以A∈α,B∈α.又因为A∈l,B∈l,
所以l?α.因为b∥c,
所以b,c确定一个平面β.
同理可证l?β.于是b?α,l?α,b?β,l?β,
即α∩β=b,α∩β=l.
又因为b与l不重合,所以α与β重合,所以a,b,c,l共面.2.已知四条直线两两相交,且不共点,求证:这四条直线在同一平面内.已知:a,b,c,d四条直线两两相交,且不共点,
求证:a,b,c,d四线共面.
证明:(1)若a,b,c三线共点于O,
如图所示,因为O?d,
所以经过d与点O有且只有一个平面α.
因为A,B,C分别是d与a,b,c的交点,
所以A,B,C三点在平面α内.
由公理1知a,b,c都在平面α内,
故a,b,c,d共面.(2)若a,b,c,d无三线共点,如图所示,
因为a∩b=A,
所以经过a,b有且仅有一个平面α,
所以B,C∈α.
由公理1知c?α.
同理,d?α,从而有a,b,c,d共面.
综上所述,四条直线两两相交,且不共点,这四条直线在同一平面内.题型三 多点共线、多线共点问题
[例3] (12分)如图,在正方体ABCD-A1B1C1D1中,点M,N,E,F分别是棱CD,AB, DD1,AA1上的点,若MN与EF交于点Q,求证:D,A,Q三点共线.规范解答:因为MN∩EF=Q,
所以Q∈直线MN,Q∈直线EF,……………………2分
又因为M∈直线CD,N∈直线AB,
CD?平面ABCD,AB?平面ABCD.
所以M,N∈平面ABCD,………………………………5分
所以MN?平面ABCD.
所以Q∈平面ABCD.………………………………7分
同理,可得EF?平面ADD1A1.
所以Q∈平面ADD1A1,………………………………9分
又因为平面ABCD∩平面ADD1A1=AD,
所以Q∈直线AD,
即D,A,Q三点共线.………………………………12分一题多变:本例中,若设线段A1C与平面ABC1D1交于点Q,求证:B,Q,D1三点
共线.证明:如图,连接A1B,CD1,显然B∈平面A1BCD1,
D1∈平面A1BCD1.所以BD1?平面A1BCD1.
同理BD1?平面ABC1D1.
所以平面ABC1D1∩平面A1BCD1=BD1.
因为A1C∩平面ABC1D1=Q,
所以Q∈平面ABC1D1.
又因为A1C?平面A1BCD1,
所以Q∈平面A1BCD1.
所以Q在平面A1BCD1与ABC1D1的交线上,
即Q∈BD1,所以B,Q,D1三点共线.方法技巧点共线与线共点的证明方法:
(1)点共线:证明多点共线通常利用公理3,即两相交平面交线的唯一性,通过证明点分别在两个平面内,证明点在相交平面的交线上,也可选择其中两点确定一条直线,然后证明其他点也在其上.
(2)三线共点:证明三线共点问题可把其中一条作为分别过其余两条直线的两个平面的交线,然后再证两条直线的交点在此直线上,此外还可先将其中一条直线看作某两个平面的交线,证明该交线与另两条直线分别交于两点,再证点重合,从而得三线共点.[备用例3]
三个平面两两相交于三条直线,若这三条直线不平行,求证:这三条直线交于一点.已知平面α,β,γ两两相交于三条直线l1,l2,l3,且l1,l2,l3不平行.
求证:l1,l2,l3相交于一点.
证明:如图,α∩β=l1,β∩γ=l2,α∩γ=l3,
因为l1?β,l2?β,且l1,l2不平行,
所以l1与l2必相交.
设l1∩l2=P,则P∈l1?α,P∈l2?γ,
所以P∈α∩γ=l3.
所以l1,l2,l3相交于一点.课堂达标解析:几何中的平面是无限延展的,不可进行所有类型的度量,容易判断所有命题都不对.1.下列命题中正确的个数是( )
①一个平面长4米,宽2米;
②2个平面重叠在一起比一个平面厚;
③一个平面的面积是25平方米;
④将一个平面内的一条直线延长,它就会伸出这个平面.
(A)0 (B)1 (C)2 (D)3A解析:A.不是公理,是个常用的结论,需经过推理论证;B,C,D都是平面的基本性质公理.2.在下列命题中,不是公理的是( )
(A)平行于同一个平面的两个平面相互平行
(B)过不在同一条直线上的三点,有且只有一个平面
(C)如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内
(D)如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线A解析:因为A∈α,A∈β,所以A∈α∩β.
由公理可知α∩β为经过A的一条直线而不是A.
故α∩β=A错误.3.已知α,β为平面,A,B,M,N为点,a为直线,下列推理错误的是( )
(A)A∈a,A∈β,B∈a,B∈β?a?β
(B)M∈α,M∈β,N∈α,N∈β?α∩β=MN
(C)A∈α,A∈β?α∩β=A
(D)A,B,M∈α,A,B,M∈β,且A,B,M不共线?α,β重合C4.设平面α与平面β交于直线l,A∈α,B∈α,且直线AB∩l=C,则直线AB∩β= .?解析:因为α∩β=l,AB∩l=C,
所以C∈β,C∈AB,
所以AB∩β=C.
答案:C
