人教A版高中数学必修二 课件 2.1.2 空间中直线与直线之间的位置关系 :41张PPT
文档属性
| 名称 | 人教A版高中数学必修二 课件 2.1.2 空间中直线与直线之间的位置关系 :41张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 00:00:00 | ||
图片预览










文档简介
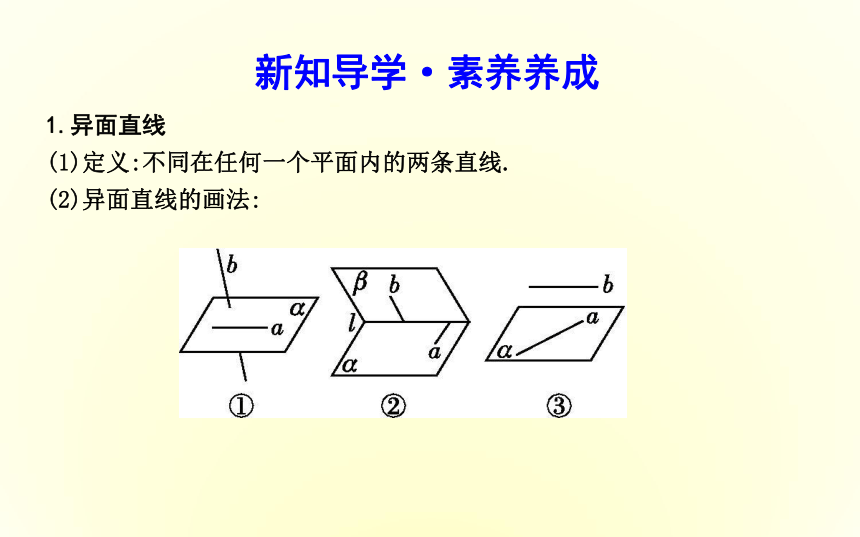
课件41张PPT。2.1.2 空间中直线与直线之间的位置关系目标导航新知导学·素养养成1.异面直线
(1)定义:不同在任何一个平面内的两条直线.
(2)异面直线的画法:2.空间两条直线的位置关系一个没有没有思考1:分别在两个平面中的两条直线是异面直线吗?
答案:不一定.如图中,虽然有a?α,b?β,即a,b分别在两个不同的平面内,但是因为a∩b=O,所以a与b不是异面直线.3.平行公理(公理4)
(1)文字表述:平行于同一条直线的两条直线互相 .这一性质叫做空间平行线的 .平行传递性a∥c4.等角定理
空间中如果两个角的两边分别对应 ,那么这两个角 或 .
5.异面直线所成的角
(1)定义:已知两条异面直线a,b,经过空间任一点O作直线a′∥a, b′∥b,我们把a′与b′所成的 (或 )叫做异面直线a与b所成的角(或夹角).平行相等互补锐角直角90°(2)异面直线所成的角θ的取值范围:0°<θ≤90°.
(3)当θ= 时,a与b互相垂直,记作 .
思考2:垂直于同一条直线的两条直线一定平行吗?
答案:不一定.在平面内此结论是正确的,但在空间中也可能异面或相交.如长方体一角的三条棱.a⊥b名师点津(1)异面直线的定义表明异面直线不具备确定平面的条件.异面直线既不相交,也不平行.
(2)异面直线所成角的范围是0°<θ≤90°,所以垂直有两种情况:异面垂直和相交垂直.
(3)公理4也称为平行公理,表明空间的平行具有传递性,它在直线、平面的平行关系中得到了广泛的应用.
(4)过平面外一点和平面内一点的直线与平面内不经过该点的直线是异面直线.此结论可作为判定两直线是否为异面直线的依据.课堂探究·素养提升题型一 空间位置关系的判断
[例1] 正方体ABCD-A1B1C1D1中,判断下列直线的位置关系:
(1)直线A1B与直线D1C的位置关系是 ;?
(2)直线A1B与直线B1C的位置关系是 ;?
(3)直线D1D与直线D1C的位置关系是 ;?
(4)直线AB与直线B1C的位置关系是 .?解:直线D1D与直线D1C显然相交于D1点,所以(3)应该填“相交”;直线A1B与直线D1C在平面A1BCD1中,且没有交点,则两直线“平行”,所以(1)应该填“平行”;点A1,B,B1在一个平面A1BB1内,而C不在平面A1BB1内,且B1?A1B,则直线A1B与直线B1C“异面”.同理,直线AB与直线B1C“异面”.所以(2)(4)都应该填“异面”.答案:(1)平行 (2)异面 (3)相交 (4)异面方法技巧(1)判定两条直线平行或相交的方法
判定两条直线平行或相交可用平面几何的方法去判断,而两条直线平行也可以用公理4判断.
(2)判定两条直线是异面直线的方法
①定义法:由定义判断两直线不可能在同一平面内.
②重要结论:连接平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.用符号语言可表示为A?α,B∈α,l?α,B?l?AB与l是异面直线(如图).解析:若a∥b,a,c是异面直线,那么b与c不可能平行,否则由公理4知a∥ c.故选C.即时训练1-1:若直线a,b,c满足a∥b,a,c异面,则b与c( )
(A)一定是异面直线
(B)一定是相交直线
(C)不可能是平行直线
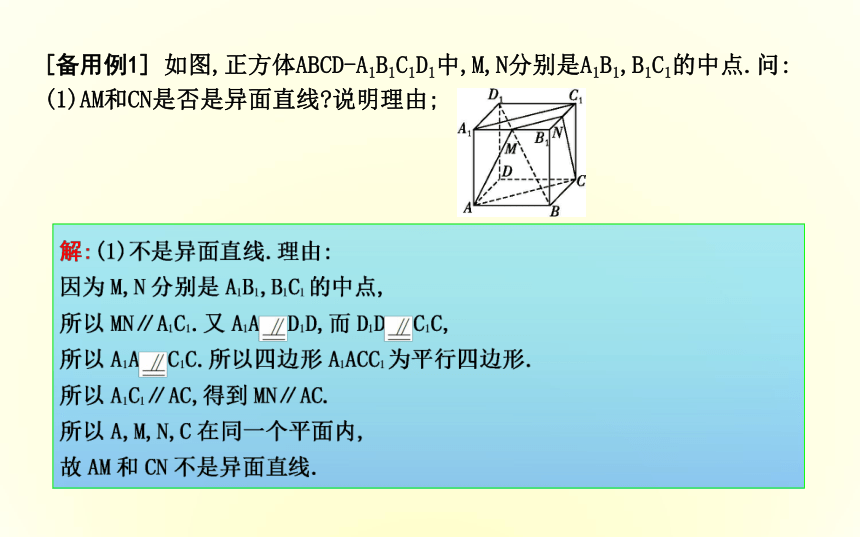
(D)不可能是相交直线[备用例1] 如图,正方体ABCD-A1B1C1D1中,M,N分别是A1B1,B1C1的中点.问:
(1)AM和CN是否是异面直线?说明理由;(2)D1B和CC1是否是异面直线?说明理由.解:(2)是异面直线.证明如下:
假设D1B与CC1在同一个平面D1CC1内,
则B∈平面CC1D1,C∈平面CC1D1,
所以BC?平面CC1D1.
而BC⊥平面CC1D1,
即BC?平面CC1D1,
所以假设不成立,
故D1B与CC1是异面直线.题型二 公理4及等角定理的应用
[例2] 在如图所示的正方体ABCD-A1B1C1D1中,E,F,E1,F1分别是棱AB,AD, B1C1,C1D1的中点,(2)∠EA1F=∠E1CF1.一题多变:将本例变为:M,M1分别是棱AD和A1D1的中点.
(1)求证:四边形BB1M1M为平行四边形;证明:(1)因为ABCD-A1B1C1D1为正方体.
所以AD=A1D1,且AD∥A1D1,
又M,M1分别为棱AD,A1D1的中点,
所以AM=A1M1且AM∥A1M1,
所以四边形AMM1A1为平行四边形,
所以M1M=AA1且M1M∥AA1.
又AA1=BB1且AA1∥BB1,
所以MM1=BB1且MM1∥BB1,
所以四边形BB1M1M为平行四边形.(2)求证:∠BMC=∠B1M1C1.证明:(2)法一 由(1)知四边形BB1M1M为平行四边形,
所以B1M1∥BM.
同理可得四边形CC1M1M为平行四边形,
所以C1M1∥CM.由平面几何知识可知,
∠BMC和∠B1M1C1都是锐角.所以∠BMC=∠B1M1C1.
法二 由(1)知四边形BB1M1M为平行四边形,
所以B1M1=BM.
同理可得四边形CC1M1M为平行四边形,
所以C1M1=CM.又因为B1C1=BC,
所以△BCM≌△B1C1M1,所以∠BMC=∠B1M1C1.方法技巧(1)空间两条直线平行的证明:一是定义法:即证明两条直线在同一个平面内且两直线没有公共点;二是利用平面图形的有关平行的性质,如三角形中位线,梯形中位线,平行四边形等关于平行的性质;三是利用公理4:找到一条直线,使所证的直线都与这条直线平行.
(2)求证角相等:一是用等角定理;二是用三角形全等或相似.[备用例2]
1.如图,已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.
(1)求证:E,F,G,H四点共面;证明:(1)在△ABD中,
因为E,H分别是AB,AD的中点,
所以EH∥BD.
同理FG∥BD,则EH∥FG.
故E,F,G,H四点共面.(2)若四边形EFGH是矩形,求证:AC⊥BD.证明:(2)由(1)知EH∥BD,同理AC∥GH.
又因为四边形EFGH是矩形,
所以EH⊥GH.故AC⊥BD.方法技巧求两异面直线所成的角的三个步骤
(1)作:根据所成角的定义,用平移法作出异面直线所成的角.
(2)证:证明作出的角就是要求的角.
(3)计算:求角的值,常利用解三角形得出.
可用“一作二证三计算”来概括.同时注意异面直线所成角θ的取值的范围是0°<θ≤90°.即时训练3-1:(1)如图,在正方体ABCD-A1B1C1D1中,异面直线AC与B1C1所成的角是( )
(A)30° (B)45°
(C)60° (D)90°解析:(1)因为B1C1∥BC,
所以∠ACB是异面直线AC与B1C1所成的角(或所成角的补角),
因为AB⊥BC,AB=BC,
所以∠ACB=45°,
所以异面直线AC与B1C1所成的角为45°.
故选B.解析:(2)连接BE,
因为在正方体ABCD-A1B1C1D1中,
E为棱CC1的中点,
所以CD∥AB,
所以∠BAE是异面直线AE与CD所成角(或所成角的补角),
设正方体ABCD-A1B1C1D1的棱长为2,解析:由题意,点P是线段AD1的中点,
连接BC1,可得AD1∥BC1.
异面直线CP与BC1所成的角的平面角为∠CPA.
连接AC,在△CPA中,2.如图,已知长方体ABCD-A1B1C1D1中,A1A=AB,E,F分别是BD1和AD的中点,求异面直线CD1,EF所成的角的大小.所以EF∥DG,
所以∠DGD1(或其补角)是异面直线CD1与EF所成的角.
又因为A1A=AB,
所以四边形ABB1A1,四边形CDD1C1都是正方形,
且G为CD1的中点,
所以DG⊥CD1,
所以∠D1GD=90°,
所以异面直线CD1,EF所成的角为90°.课堂达标解析:对于A,空间两条不相交的直线有两种可能,一是平行(共面),另一个是异面.所以A应排除.对于B,分别位于两个平面内的直线,既可能平行也可能相交也可异面,如图,就是相交的情况,所以B应排除.对于C,如图的a,b可看作是平面α内的一条直线a与平面α外的一条直线b,显然它们是相交直线,所以C应排除.只有D符合定义.所以应选D.1.异面直线是指( )
(A)空间中两条不相交的直线
(B)分别位于两个不同平面内的两条直线
(C)平面内的一条直线与平面外的一条直线
(D)不同在任何一个平面内的两条直线D解析:如图,在正方体ABCD-A1B1C1D1中,AA1与BC是异面直线,又AA1∥BB1, AA1∥DD1,显然BB1∩BC=B,DD1与BC是异面直线,故选B.2.一条直线与两条异面直线中的一条平行,则它和另一条的位置关系是( )
(A)平行或异面 (B)相交或异面
(C)异面 (D)相交B解析:由等角定理可知∠PQR与∠ABC相等或互补,故∠PQR=30°或150°.3.已知AB∥PQ,BC∥QR,若∠ABC=30°,则∠PQR等于( )
(A)30° (B)30°或150°
(C)150° (D)以上结论都不对B答案:平行5.在正方体ABCD-A1B1C1D1中,E为C1D1的中点,则异面直线AE与A1B1所成的角的余弦值为 .?
(1)定义:不同在任何一个平面内的两条直线.
(2)异面直线的画法:2.空间两条直线的位置关系一个没有没有思考1:分别在两个平面中的两条直线是异面直线吗?
答案:不一定.如图中,虽然有a?α,b?β,即a,b分别在两个不同的平面内,但是因为a∩b=O,所以a与b不是异面直线.3.平行公理(公理4)
(1)文字表述:平行于同一条直线的两条直线互相 .这一性质叫做空间平行线的 .平行传递性a∥c4.等角定理
空间中如果两个角的两边分别对应 ,那么这两个角 或 .
5.异面直线所成的角
(1)定义:已知两条异面直线a,b,经过空间任一点O作直线a′∥a, b′∥b,我们把a′与b′所成的 (或 )叫做异面直线a与b所成的角(或夹角).平行相等互补锐角直角90°(2)异面直线所成的角θ的取值范围:0°<θ≤90°.
(3)当θ= 时,a与b互相垂直,记作 .
思考2:垂直于同一条直线的两条直线一定平行吗?
答案:不一定.在平面内此结论是正确的,但在空间中也可能异面或相交.如长方体一角的三条棱.a⊥b名师点津(1)异面直线的定义表明异面直线不具备确定平面的条件.异面直线既不相交,也不平行.
(2)异面直线所成角的范围是0°<θ≤90°,所以垂直有两种情况:异面垂直和相交垂直.
(3)公理4也称为平行公理,表明空间的平行具有传递性,它在直线、平面的平行关系中得到了广泛的应用.
(4)过平面外一点和平面内一点的直线与平面内不经过该点的直线是异面直线.此结论可作为判定两直线是否为异面直线的依据.课堂探究·素养提升题型一 空间位置关系的判断
[例1] 正方体ABCD-A1B1C1D1中,判断下列直线的位置关系:
(1)直线A1B与直线D1C的位置关系是 ;?
(2)直线A1B与直线B1C的位置关系是 ;?
(3)直线D1D与直线D1C的位置关系是 ;?
(4)直线AB与直线B1C的位置关系是 .?解:直线D1D与直线D1C显然相交于D1点,所以(3)应该填“相交”;直线A1B与直线D1C在平面A1BCD1中,且没有交点,则两直线“平行”,所以(1)应该填“平行”;点A1,B,B1在一个平面A1BB1内,而C不在平面A1BB1内,且B1?A1B,则直线A1B与直线B1C“异面”.同理,直线AB与直线B1C“异面”.所以(2)(4)都应该填“异面”.答案:(1)平行 (2)异面 (3)相交 (4)异面方法技巧(1)判定两条直线平行或相交的方法
判定两条直线平行或相交可用平面几何的方法去判断,而两条直线平行也可以用公理4判断.
(2)判定两条直线是异面直线的方法
①定义法:由定义判断两直线不可能在同一平面内.
②重要结论:连接平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.用符号语言可表示为A?α,B∈α,l?α,B?l?AB与l是异面直线(如图).解析:若a∥b,a,c是异面直线,那么b与c不可能平行,否则由公理4知a∥ c.故选C.即时训练1-1:若直线a,b,c满足a∥b,a,c异面,则b与c( )
(A)一定是异面直线
(B)一定是相交直线
(C)不可能是平行直线
(D)不可能是相交直线[备用例1] 如图,正方体ABCD-A1B1C1D1中,M,N分别是A1B1,B1C1的中点.问:
(1)AM和CN是否是异面直线?说明理由;(2)D1B和CC1是否是异面直线?说明理由.解:(2)是异面直线.证明如下:
假设D1B与CC1在同一个平面D1CC1内,
则B∈平面CC1D1,C∈平面CC1D1,
所以BC?平面CC1D1.
而BC⊥平面CC1D1,
即BC?平面CC1D1,
所以假设不成立,
故D1B与CC1是异面直线.题型二 公理4及等角定理的应用
[例2] 在如图所示的正方体ABCD-A1B1C1D1中,E,F,E1,F1分别是棱AB,AD, B1C1,C1D1的中点,(2)∠EA1F=∠E1CF1.一题多变:将本例变为:M,M1分别是棱AD和A1D1的中点.
(1)求证:四边形BB1M1M为平行四边形;证明:(1)因为ABCD-A1B1C1D1为正方体.
所以AD=A1D1,且AD∥A1D1,
又M,M1分别为棱AD,A1D1的中点,
所以AM=A1M1且AM∥A1M1,
所以四边形AMM1A1为平行四边形,
所以M1M=AA1且M1M∥AA1.
又AA1=BB1且AA1∥BB1,
所以MM1=BB1且MM1∥BB1,
所以四边形BB1M1M为平行四边形.(2)求证:∠BMC=∠B1M1C1.证明:(2)法一 由(1)知四边形BB1M1M为平行四边形,
所以B1M1∥BM.
同理可得四边形CC1M1M为平行四边形,
所以C1M1∥CM.由平面几何知识可知,
∠BMC和∠B1M1C1都是锐角.所以∠BMC=∠B1M1C1.
法二 由(1)知四边形BB1M1M为平行四边形,
所以B1M1=BM.
同理可得四边形CC1M1M为平行四边形,
所以C1M1=CM.又因为B1C1=BC,
所以△BCM≌△B1C1M1,所以∠BMC=∠B1M1C1.方法技巧(1)空间两条直线平行的证明:一是定义法:即证明两条直线在同一个平面内且两直线没有公共点;二是利用平面图形的有关平行的性质,如三角形中位线,梯形中位线,平行四边形等关于平行的性质;三是利用公理4:找到一条直线,使所证的直线都与这条直线平行.
(2)求证角相等:一是用等角定理;二是用三角形全等或相似.[备用例2]
1.如图,已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.
(1)求证:E,F,G,H四点共面;证明:(1)在△ABD中,
因为E,H分别是AB,AD的中点,
所以EH∥BD.
同理FG∥BD,则EH∥FG.
故E,F,G,H四点共面.(2)若四边形EFGH是矩形,求证:AC⊥BD.证明:(2)由(1)知EH∥BD,同理AC∥GH.
又因为四边形EFGH是矩形,
所以EH⊥GH.故AC⊥BD.方法技巧求两异面直线所成的角的三个步骤
(1)作:根据所成角的定义,用平移法作出异面直线所成的角.
(2)证:证明作出的角就是要求的角.
(3)计算:求角的值,常利用解三角形得出.
可用“一作二证三计算”来概括.同时注意异面直线所成角θ的取值的范围是0°<θ≤90°.即时训练3-1:(1)如图,在正方体ABCD-A1B1C1D1中,异面直线AC与B1C1所成的角是( )
(A)30° (B)45°
(C)60° (D)90°解析:(1)因为B1C1∥BC,
所以∠ACB是异面直线AC与B1C1所成的角(或所成角的补角),
因为AB⊥BC,AB=BC,
所以∠ACB=45°,
所以异面直线AC与B1C1所成的角为45°.
故选B.解析:(2)连接BE,
因为在正方体ABCD-A1B1C1D1中,
E为棱CC1的中点,
所以CD∥AB,
所以∠BAE是异面直线AE与CD所成角(或所成角的补角),
设正方体ABCD-A1B1C1D1的棱长为2,解析:由题意,点P是线段AD1的中点,
连接BC1,可得AD1∥BC1.
异面直线CP与BC1所成的角的平面角为∠CPA.
连接AC,在△CPA中,2.如图,已知长方体ABCD-A1B1C1D1中,A1A=AB,E,F分别是BD1和AD的中点,求异面直线CD1,EF所成的角的大小.所以EF∥DG,
所以∠DGD1(或其补角)是异面直线CD1与EF所成的角.
又因为A1A=AB,
所以四边形ABB1A1,四边形CDD1C1都是正方形,
且G为CD1的中点,
所以DG⊥CD1,
所以∠D1GD=90°,
所以异面直线CD1,EF所成的角为90°.课堂达标解析:对于A,空间两条不相交的直线有两种可能,一是平行(共面),另一个是异面.所以A应排除.对于B,分别位于两个平面内的直线,既可能平行也可能相交也可异面,如图,就是相交的情况,所以B应排除.对于C,如图的a,b可看作是平面α内的一条直线a与平面α外的一条直线b,显然它们是相交直线,所以C应排除.只有D符合定义.所以应选D.1.异面直线是指( )
(A)空间中两条不相交的直线
(B)分别位于两个不同平面内的两条直线
(C)平面内的一条直线与平面外的一条直线
(D)不同在任何一个平面内的两条直线D解析:如图,在正方体ABCD-A1B1C1D1中,AA1与BC是异面直线,又AA1∥BB1, AA1∥DD1,显然BB1∩BC=B,DD1与BC是异面直线,故选B.2.一条直线与两条异面直线中的一条平行,则它和另一条的位置关系是( )
(A)平行或异面 (B)相交或异面
(C)异面 (D)相交B解析:由等角定理可知∠PQR与∠ABC相等或互补,故∠PQR=30°或150°.3.已知AB∥PQ,BC∥QR,若∠ABC=30°,则∠PQR等于( )
(A)30° (B)30°或150°
(C)150° (D)以上结论都不对B答案:平行5.在正方体ABCD-A1B1C1D1中,E为C1D1的中点,则异面直线AE与A1B1所成的角的余弦值为 .?
