人教A版高中数学必修二 课件 2.2.1 直线与平面平行的判定 :16张PPT
文档属性
| 名称 | 人教A版高中数学必修二 课件 2.2.1 直线与平面平行的判定 :16张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 00:00:00 | ||
图片预览




文档简介
课件16张PPT。2.2 直线、平面平行的判定及其性质
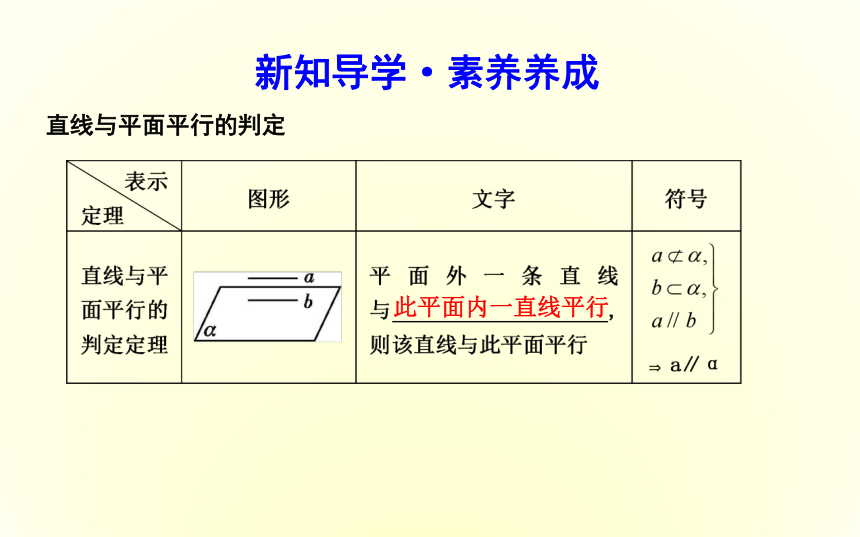
2.2.1 直线与平面平行的判定目标导航新知导学·素养养成直线与平面平行的判定此平面内一直线平行名师点津(1)用该定理判断直线a和平面α平行时,必须同时具备三个条件:
①直线a在平面α外,即a?α;
②直线b在平面α内,即b?α;
③两直线a,b平行,即a∥b.
(2)该定理的作用:证明线面平行.
(3)应用时,只需在平面内找到一条直线与已知直线平行即可.课堂探究·素养提升题型一 线面平行的判定定理的理解
[例1]下列说法中正确的是( )
(A)若直线l平行于平面α内的无数条直线,则l∥α
(B)若直线a在平面α外,则a∥α
(C)若直线a∥b,b?α,则a∥α
(D)若直线a∥b,b?α,那么直线a平行于平面α内的无数条直线解析:选项A中,直线l?α时l与α不平行;
直线在平面外包括直线与平面平行和直线与平面相交两种情况,所以选项B不正确;
选项C中直线a可能在平面α内;
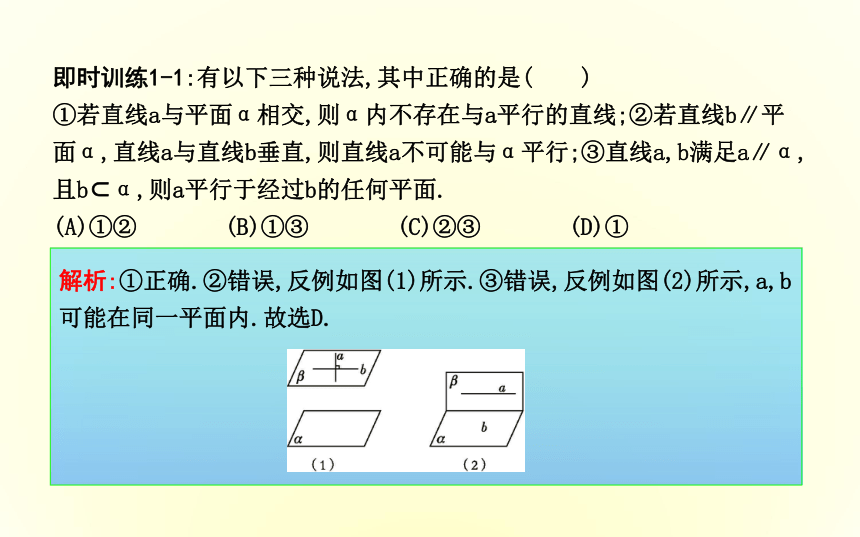
选项D正确.故选D.解析:①正确.②错误,反例如图(1)所示.③错误,反例如图(2)所示,a,b可能在同一平面内.故选D.即时训练1-1:有以下三种说法,其中正确的是( )
①若直线a与平面α相交,则α内不存在与a平行的直线;②若直线b∥平面α,直线a与直线b垂直,则直线a不可能与α平行;③直线a,b满足a∥α,且b?α,则a平行于经过b的任何平面.
(A)①② (B)①③ (C)②③ (D)①方法技巧(1)利用直线与平面平行的判定定理证明线面平行,关键是寻找平面内与已知直线平行的直线.
(2)证线线平行的方法常用三角形中位线定理、平行四边形性质、平行线分线段成比例定理、平行公理等.即时训练2-1:如图,四边形ABCD是平行四边形,S是平面ABCD外一点,M为SC的中点,求证:SA∥平面MDB.证明:连接AC交BD于点O,连接OM.
因为M为SC的中点,O为AC的中点,所以OM∥SA,
因为OM?平面MDB,SA?平面MDB,
所以SA∥平面MDB.[备用例题]
已知公共边为AB的两个全等的矩形ABCD和ABEF不在同一平面内,P,Q分别是对角线AE,BD上的点,且AP=DQ(如图).求证:PQ∥平面CBE.课堂达标B1.下列命题:
①如果一条直线不在平面内,则这条直线就与这个平面平行;
②过直线外一点,可以作无数个平面与这条直线平行;
③如果一条直线与平面平行,则它与平面内的任何直线平行.
其中正确命题的个数为( )
(A)0个 (B)1个 (C)2个 (D)3个解析:①中,直线可能与平面相交,故①错;②是正确的;③中,一条直线与平面平行,则它与内的直线平行或异面,故③错.2.如果两直线a,b相交,且a∥平面α,那么b与平面α的位置关系是( )
(A)b∥α (B)b∥α或b与α相交 (C)b与α相交 (D)b?α
3.若线段AB,BC,CD不共面,M,N,P分别为它们的中点,则直线BD与平面MNP的位置关系为( )
(A)平行 (B)可能相交
(C)相交 (D)可能垂直BA解析:因为N,P分别为BC,CD的中点,所以NP∥BD.因为NP?平面MNP,BD?平面MNP,所以BD∥平面MNP.故选A.4.(2018·福州高一检测)平面α与△ABC的两边AB,AC分别交于点D,E,且AD∶DB=AE∶EC,如图,则BC与α的位置关系是( )
(A)平行 (B)相交
(C)平行或相交 (D)异面A解析:因为AD∶DB=AE∶EC,所以DE∥BC,又DE?α,BC?α,所以BC∥α.故选A.5.能保证直线a与平面α平行的条件是( )
(A)b?α,a∥b
(B)b?α,c∥α,a∥b,a∥c
(C)b?α,A,B∈a,C,D∈b,且AC=BD
(D)a?α,b?α,a∥bD解析:A错误,若b?α,a∥b,则a∥α或a?α;B错误;若b?α,c∥α, a∥b,a∥c,则a∥α或a?α;C错误;若满足此条件,则a∥α或a?α或a与α相交;D正确,恰好是定理所具备的不可缺少的三个条件.故选D.
2.2.1 直线与平面平行的判定目标导航新知导学·素养养成直线与平面平行的判定此平面内一直线平行名师点津(1)用该定理判断直线a和平面α平行时,必须同时具备三个条件:
①直线a在平面α外,即a?α;
②直线b在平面α内,即b?α;
③两直线a,b平行,即a∥b.
(2)该定理的作用:证明线面平行.
(3)应用时,只需在平面内找到一条直线与已知直线平行即可.课堂探究·素养提升题型一 线面平行的判定定理的理解
[例1]下列说法中正确的是( )
(A)若直线l平行于平面α内的无数条直线,则l∥α
(B)若直线a在平面α外,则a∥α
(C)若直线a∥b,b?α,则a∥α
(D)若直线a∥b,b?α,那么直线a平行于平面α内的无数条直线解析:选项A中,直线l?α时l与α不平行;
直线在平面外包括直线与平面平行和直线与平面相交两种情况,所以选项B不正确;
选项C中直线a可能在平面α内;
选项D正确.故选D.解析:①正确.②错误,反例如图(1)所示.③错误,反例如图(2)所示,a,b可能在同一平面内.故选D.即时训练1-1:有以下三种说法,其中正确的是( )
①若直线a与平面α相交,则α内不存在与a平行的直线;②若直线b∥平面α,直线a与直线b垂直,则直线a不可能与α平行;③直线a,b满足a∥α,且b?α,则a平行于经过b的任何平面.
(A)①② (B)①③ (C)②③ (D)①方法技巧(1)利用直线与平面平行的判定定理证明线面平行,关键是寻找平面内与已知直线平行的直线.
(2)证线线平行的方法常用三角形中位线定理、平行四边形性质、平行线分线段成比例定理、平行公理等.即时训练2-1:如图,四边形ABCD是平行四边形,S是平面ABCD外一点,M为SC的中点,求证:SA∥平面MDB.证明:连接AC交BD于点O,连接OM.
因为M为SC的中点,O为AC的中点,所以OM∥SA,
因为OM?平面MDB,SA?平面MDB,
所以SA∥平面MDB.[备用例题]
已知公共边为AB的两个全等的矩形ABCD和ABEF不在同一平面内,P,Q分别是对角线AE,BD上的点,且AP=DQ(如图).求证:PQ∥平面CBE.课堂达标B1.下列命题:
①如果一条直线不在平面内,则这条直线就与这个平面平行;
②过直线外一点,可以作无数个平面与这条直线平行;
③如果一条直线与平面平行,则它与平面内的任何直线平行.
其中正确命题的个数为( )
(A)0个 (B)1个 (C)2个 (D)3个解析:①中,直线可能与平面相交,故①错;②是正确的;③中,一条直线与平面平行,则它与内的直线平行或异面,故③错.2.如果两直线a,b相交,且a∥平面α,那么b与平面α的位置关系是( )
(A)b∥α (B)b∥α或b与α相交 (C)b与α相交 (D)b?α
3.若线段AB,BC,CD不共面,M,N,P分别为它们的中点,则直线BD与平面MNP的位置关系为( )
(A)平行 (B)可能相交
(C)相交 (D)可能垂直BA解析:因为N,P分别为BC,CD的中点,所以NP∥BD.因为NP?平面MNP,BD?平面MNP,所以BD∥平面MNP.故选A.4.(2018·福州高一检测)平面α与△ABC的两边AB,AC分别交于点D,E,且AD∶DB=AE∶EC,如图,则BC与α的位置关系是( )
(A)平行 (B)相交
(C)平行或相交 (D)异面A解析:因为AD∶DB=AE∶EC,所以DE∥BC,又DE?α,BC?α,所以BC∥α.故选A.5.能保证直线a与平面α平行的条件是( )
(A)b?α,a∥b
(B)b?α,c∥α,a∥b,a∥c
(C)b?α,A,B∈a,C,D∈b,且AC=BD
(D)a?α,b?α,a∥bD解析:A错误,若b?α,a∥b,则a∥α或a?α;B错误;若b?α,c∥α, a∥b,a∥c,则a∥α或a?α;C错误;若满足此条件,则a∥α或a?α或a与α相交;D正确,恰好是定理所具备的不可缺少的三个条件.故选D.
