人教A版高中数学必修二 课件 2.2.3 直线与平面平行的性质 :15张PPT
文档属性
| 名称 | 人教A版高中数学必修二 课件 2.2.3 直线与平面平行的性质 :15张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 21:47:29 | ||
图片预览




文档简介
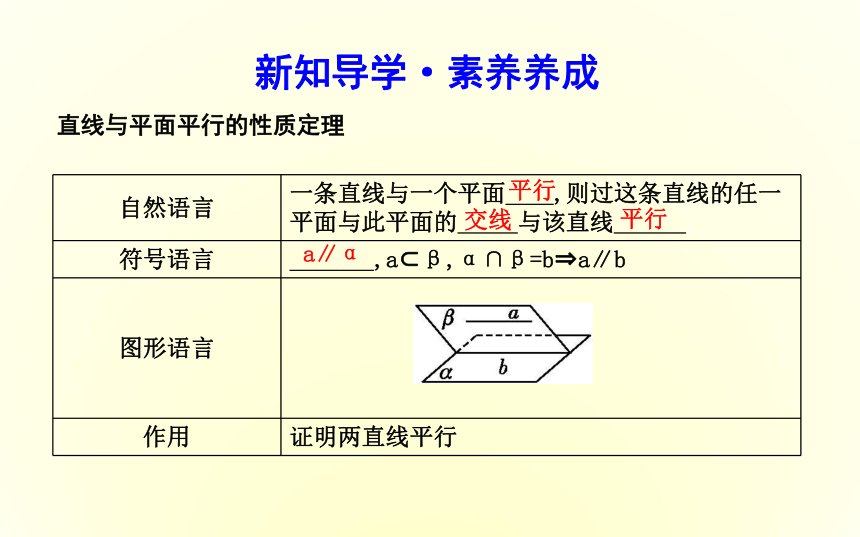
课件15张PPT。2.2.3 直线与平面平行的性质目标导航新知导学·素养养成直线与平面平行的性质定理平行交线平行a∥α 思考:若直线a∥平面α,则直线a与平面α内的直线有怎样的位置关系?
答案:平行或异面.名师点津直线与平面平行的性质定理中有三个条件:①直线a和平面α平行,即a∥α;②直线a在平面β内,即a?β;③平面α,β相交,即α∩β=b.三个条件缺一不可.课堂探究·素养提升题型一 直线与平面平行的性质定理的理解
[例1]已知直线m,n及平面α,β,有下列关系:
①m,n?β;②n?α;③m∥α;④m∥n.
现把其中的一些关系看做条件,另一些看做结论,可以组成的正确推论是 .(只写出一种情况即可)?解析:结合线面平行的性质定理,可知①②③?④.
结合线面平行的判定定理,可知①②④?③.
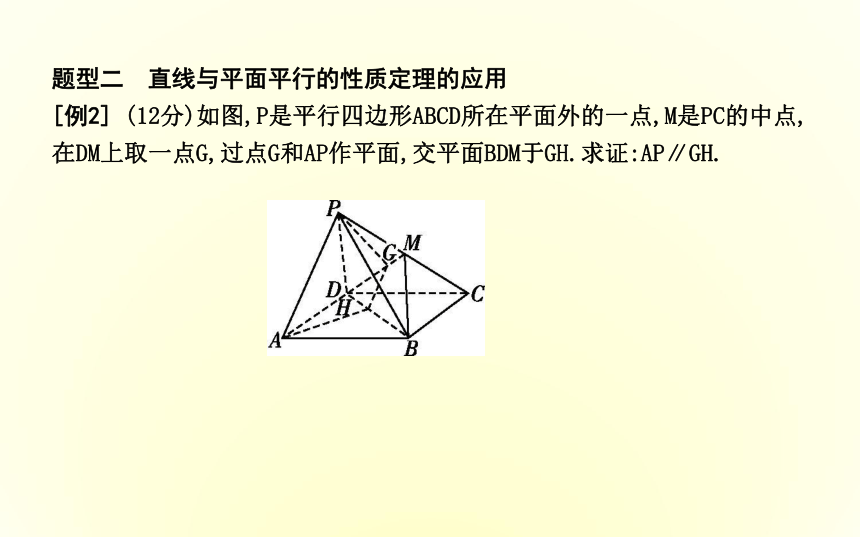
答案:①②③?④(或①②④?③)题型二 直线与平面平行的性质定理的应用
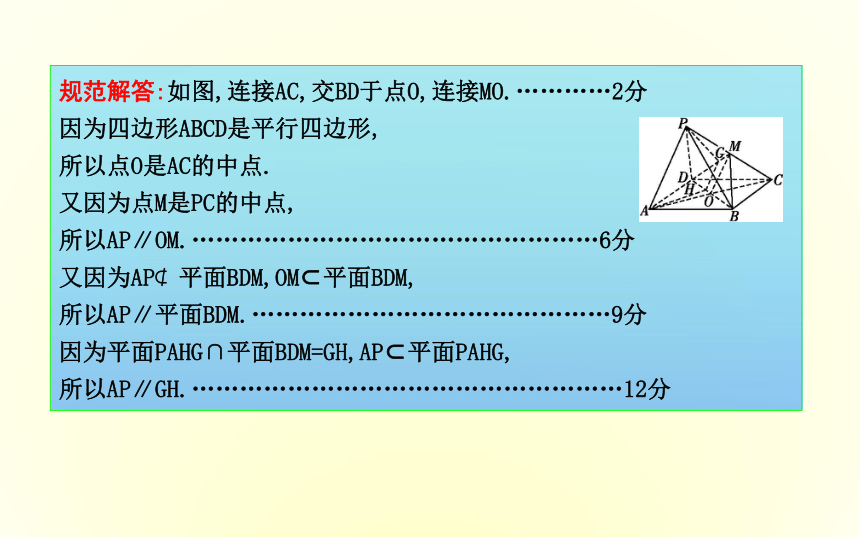
[例2] (12分)如图,P是平行四边形ABCD所在平面外的一点,M是PC的中点,在DM上取一点G,过点G和AP作平面,交平面BDM于GH.求证:AP∥GH. 规范解答:如图,连接AC,交BD于点O,连接MO.…………2分
因为四边形ABCD是平行四边形,
所以点O是AC的中点.
又因为点M是PC的中点,
所以AP∥OM.……………………………………………6分
又因为AP?平面BDM,OM?平面BDM,
所以AP∥平面BDM.………………………………………9分
因为平面PAHG∩平面BDM=GH,AP?平面PAHG,
所以AP∥GH.………………………………………………12分一题多变:(1)本例中,若平面PAD∩平面PBC=l,试证明:BC∥l;(1)证明:法一 因为BC∥AD,BC?平面PAD,AD?平面PAD,
所以BC∥平面PAD.
又因为平面PBC∩平面PAD=l,所以BC∥l.
法二 因为AD∥BC,AD?平面PBC,
BC?平面PBC,所以AD∥平面PBC.
又因为平面PBC∩平面PAD=l,
所以l∥AD,l∥BC.(2)本例中,若AB中点为N,证明:MN∥平面PAD.(2)证明:取PD的中点E,连接AE,ME,可以证得ME∥AN且ME=AN.
所以四边形ANME为平行四边形.
所以MN∥AE,
又因为MN?平面APD,AE?平面APD,
所以MN∥平面PAD.误区警示(1)欲证线线平行可转化为线面平行解决,常与判定定理结合使用;
(2)性质定理中有三个条件,缺一不可,主要平行关系的寻求,常利用中位线性质.
(3)做辅助线常用技巧:“由中点想中点,中点——中点——中位线”.课堂达标1.下列命题正确的是( )
(A)若直线a∥平面α,直线b∥平面α,则直线a∥直线b
(B)若直线a∥平面α,直线a与直线b相交,则直线b与平面α相交
(C)若直线a∥平面α,直线a∥直线b,则直线b∥平面α
(D)若直线a∥平面α,则直线a与平面α内任意一条直线都无公共点D解析:A中,直线a与直线b也可能异面、相交,所以不正确;B中,直线b也可能与平面α平行,所以不正确;C中,直线b也可能在平面α内,所以不正确;根据直线与平面平行的定义知D正确,故选D.2.已知:α∩β=b,a∥α,a∥β,则a与b的位置关系是( )
(A)a∥b
(B)a⊥b
(C)a,b相交但不垂直
(D)a,b异面A解析:设过a的平面γ,η,且α∩γ=m,β∩η=n,
则a∥m,a∥n,得m∥n,m∥β,
所以m∥b,则a∥b.
故选A.3.正方体ABCD-A1B1C1D1中,截面BA1C1与直线AC的位置关系是( )
(A)AC∥截面BA1C1
(B)AC与截面BA1C1相交
(C)AC在截面BA1C1内
(D)以上答案都错误A解析:因为AC∥A1C1,又因为AC?平面BA1C1,
所以AC∥平面BA1C1.故选A.4.如图,已知S为四边形ABCD外一点, G,H分别为SB,BD上的点,若GH∥平面SCD,则( )
(A)GH∥SA
(B)GH∥SD
(C)GH∥SC
(D)以上均有可能B解析:因为GH∥平面SCD,GH?平面SBD,平面SBD∩平面SCD=SD,所以GH∥ SD,显然GH与SA,SC均不平行,故选B.5.在正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于 .?
答案:平行或异面.名师点津直线与平面平行的性质定理中有三个条件:①直线a和平面α平行,即a∥α;②直线a在平面β内,即a?β;③平面α,β相交,即α∩β=b.三个条件缺一不可.课堂探究·素养提升题型一 直线与平面平行的性质定理的理解
[例1]已知直线m,n及平面α,β,有下列关系:
①m,n?β;②n?α;③m∥α;④m∥n.
现把其中的一些关系看做条件,另一些看做结论,可以组成的正确推论是 .(只写出一种情况即可)?解析:结合线面平行的性质定理,可知①②③?④.
结合线面平行的判定定理,可知①②④?③.
答案:①②③?④(或①②④?③)题型二 直线与平面平行的性质定理的应用
[例2] (12分)如图,P是平行四边形ABCD所在平面外的一点,M是PC的中点,在DM上取一点G,过点G和AP作平面,交平面BDM于GH.求证:AP∥GH. 规范解答:如图,连接AC,交BD于点O,连接MO.…………2分
因为四边形ABCD是平行四边形,
所以点O是AC的中点.
又因为点M是PC的中点,
所以AP∥OM.……………………………………………6分
又因为AP?平面BDM,OM?平面BDM,
所以AP∥平面BDM.………………………………………9分
因为平面PAHG∩平面BDM=GH,AP?平面PAHG,
所以AP∥GH.………………………………………………12分一题多变:(1)本例中,若平面PAD∩平面PBC=l,试证明:BC∥l;(1)证明:法一 因为BC∥AD,BC?平面PAD,AD?平面PAD,
所以BC∥平面PAD.
又因为平面PBC∩平面PAD=l,所以BC∥l.
法二 因为AD∥BC,AD?平面PBC,
BC?平面PBC,所以AD∥平面PBC.
又因为平面PBC∩平面PAD=l,
所以l∥AD,l∥BC.(2)本例中,若AB中点为N,证明:MN∥平面PAD.(2)证明:取PD的中点E,连接AE,ME,可以证得ME∥AN且ME=AN.
所以四边形ANME为平行四边形.
所以MN∥AE,
又因为MN?平面APD,AE?平面APD,
所以MN∥平面PAD.误区警示(1)欲证线线平行可转化为线面平行解决,常与判定定理结合使用;
(2)性质定理中有三个条件,缺一不可,主要平行关系的寻求,常利用中位线性质.
(3)做辅助线常用技巧:“由中点想中点,中点——中点——中位线”.课堂达标1.下列命题正确的是( )
(A)若直线a∥平面α,直线b∥平面α,则直线a∥直线b
(B)若直线a∥平面α,直线a与直线b相交,则直线b与平面α相交
(C)若直线a∥平面α,直线a∥直线b,则直线b∥平面α
(D)若直线a∥平面α,则直线a与平面α内任意一条直线都无公共点D解析:A中,直线a与直线b也可能异面、相交,所以不正确;B中,直线b也可能与平面α平行,所以不正确;C中,直线b也可能在平面α内,所以不正确;根据直线与平面平行的定义知D正确,故选D.2.已知:α∩β=b,a∥α,a∥β,则a与b的位置关系是( )
(A)a∥b
(B)a⊥b
(C)a,b相交但不垂直
(D)a,b异面A解析:设过a的平面γ,η,且α∩γ=m,β∩η=n,
则a∥m,a∥n,得m∥n,m∥β,
所以m∥b,则a∥b.
故选A.3.正方体ABCD-A1B1C1D1中,截面BA1C1与直线AC的位置关系是( )
(A)AC∥截面BA1C1
(B)AC与截面BA1C1相交
(C)AC在截面BA1C1内
(D)以上答案都错误A解析:因为AC∥A1C1,又因为AC?平面BA1C1,
所以AC∥平面BA1C1.故选A.4.如图,已知S为四边形ABCD外一点, G,H分别为SB,BD上的点,若GH∥平面SCD,则( )
(A)GH∥SA
(B)GH∥SD
(C)GH∥SC
(D)以上均有可能B解析:因为GH∥平面SCD,GH?平面SBD,平面SBD∩平面SCD=SD,所以GH∥ SD,显然GH与SA,SC均不平行,故选B.5.在正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于 .?
