人教A版高中数学必修二 课件 2.2.4 平面与平面平行的性质 :21张PPT
文档属性
| 名称 | 人教A版高中数学必修二 课件 2.2.4 平面与平面平行的性质 :21张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 21:46:27 | ||
图片预览






文档简介
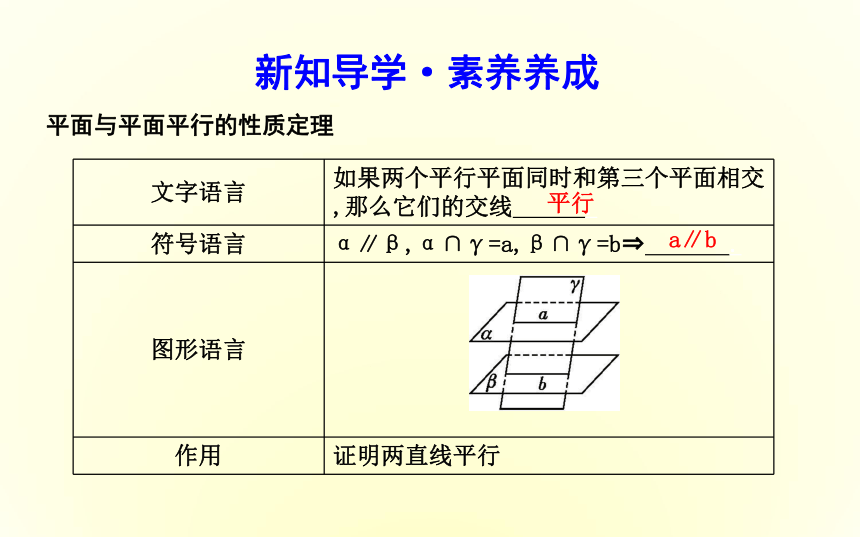
课件21张PPT。2.2.4 平面与平面平行的性质目标导航新知导学·素养养成平面与平面平行的性质定理a∥b平行思考1:若两个平面互相平行,则其中一个平面内的直线与另一个平面什么关系?与另一个平面内的直线又有何关系?
答案:若两个平面平行,其中一个平面内的直线与另一个平面平行;与另一个平面内的直线平行或异面.
思考2:平行于同一个平面的两个平面什么关系?
答案:平行.名师点津(1)已知两个平面平行,虽然一个平面内的任何直线都平行于另一个平面,但是这两个平面内的所有直线并不一定相互平行,它们可能是平行直线,也可能是异面
直线,但不可能是相交直线.
(2)该定理提供了证明线线平行的另一种方法,应用时要紧扣与两个平行平面都相交的第三个平面.课堂探究·素养提升题型一 面面平行性质定理的应用
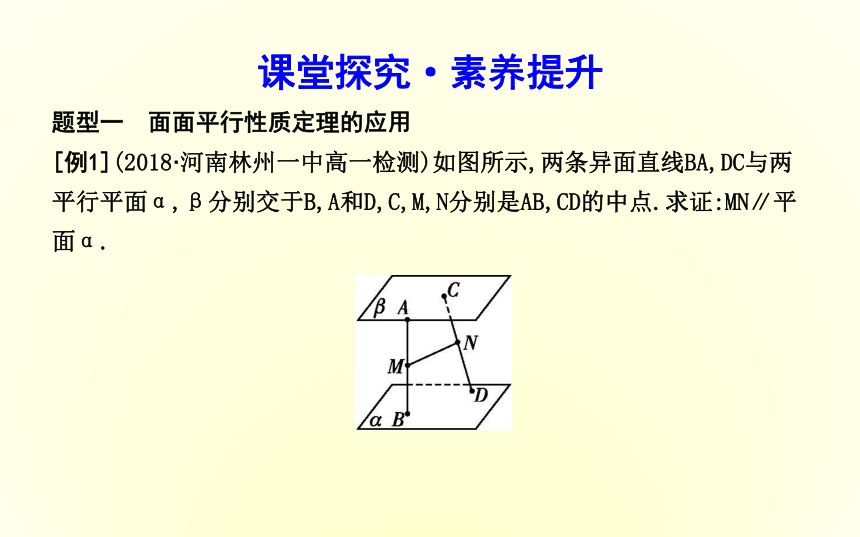
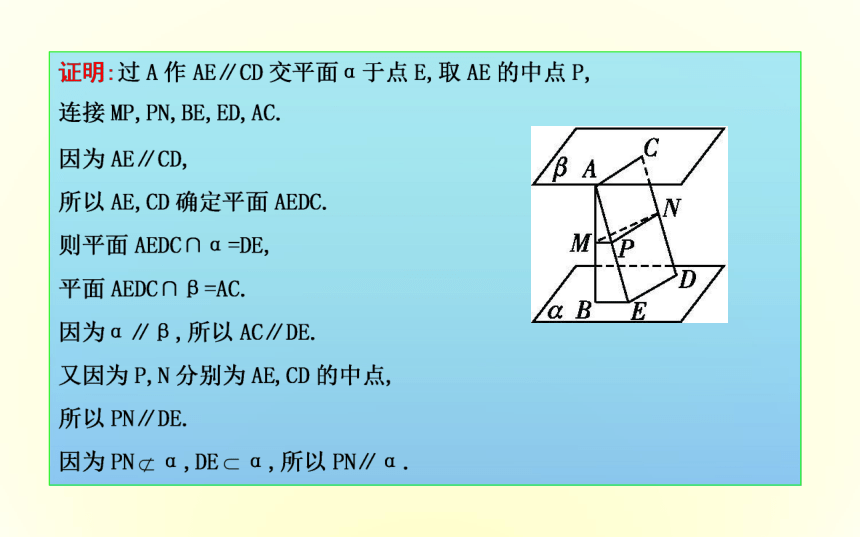
[例1](2018·河南林州一中高一检测)如图所示,两条异面直线BA,DC与两平行平面α,β分别交于B,A和D,C,M,N分别是AB,CD的中点.求证:MN∥平面α.方法技巧(1)利用面面平行的性质定理判定两直线平行的步骤:
①先找两个平面,使这两个平面分别经过这两条直线中的一条;
②判定这两个平面平行;
③再找一个平面,使这两条直线都在这个平面上;
④由性质定理得出线线平行.
(2)应用面面平行的性质定理时,往往需要“作”或“找”辅助平面,但辅助平面不可乱作,要想办法与其他已知量联系起来.即时训练1-1:如图,在三棱柱ABC-A1B1C1中,M是A1C1的中点,平面AB1M∥平面BC1N,AC∩平面BC1N=N.求证:N为AC的中点. 题型二 平行关系的综合应用
[例2]如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AD∥BC,平面A1DCE与B1B交于点E.
求证:EC∥A1D. 证明:因为BE∥AA1,
AA1?平面AA1D,BE?平面AA1D,
所以BE∥平面AA1D.
因为BC∥AD,AD?平面AA1D,
BC?平面AA1D,所以BC∥平面AA1D.
又BE∩BC=B,
BE?平面BCE,BC?平面BCE,
所以平面BCE∥平面AA1D.
又平面A1DCE∩平面BCE=EC,
平面A1DCE∩平面AA1D=A1D,
所以EC∥A1D.方法技巧要灵活应用线线平行、线面平行和面面平行的相互联系、相互转化.在解决立体几何中的平行问题时,一般都要用到平行关系的转化.转化思想是解决这类问题的最有效的方法.具体转化过程如图所示:即时训练2-1:如图,正方体ABCD-A1B1C1D1,点E在AB1上,点F在BD上,且B1E=BF.求证:EF∥平面BB1C1C.所以ME∥BB1.
因为ME?平面BB1C1C,BB1?平面BB1C1C,
所以ME∥平面BB1C1C.
由FM∥AD,AD∥BC,知FM∥BC.
而FM?平面BB1C1C,BC?平面BB1C1C,
所以FM∥平面BB1C1C.
因为FM∩ME=M.
所以平面MEF∥平面BB1C1C.
因为EF?平面MEF,
所以EF∥平面BB1C1C.课堂达标1.已知平面α∥平面β,a?α,b?β,则直线a,b的位置关系是( )
(A)平行 (B)相交
(C)异面 (D)平行或异面D解析:因为平面α∥平面β,所以平面α与平面β没有公共点.因为a?α,b?β,所以直线a,b没有公共点,所以直线a,b的位置关系是平行或异面.2.若平面α∥平面β,直线a?α,点B∈β,过点B的所有直线中( )
(A)不一定存在与a平行的直线
(B)只有两条与a平行的直线
(C)存在无数条与a平行的直线
(D)有且只有一条与a平行的直线D3.过两平行平面α,β外的点P的两条直线AB与CD,它们分别交α于A,C两点,交β于B,D两点,若PA=6,AC=9,PB=8,则BD的长为 .?答案:124.如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为 .?解析:因为平面ABFE∥平面CDHG,
又平面EFGH∩平面ABFE=EF,
平面EFGH∩平面CDHG=HG,
所以EF∥HG.
同理EH∥FG,
所以四边形EFGH的形状是平行四边形.答案:平行四边形
答案:若两个平面平行,其中一个平面内的直线与另一个平面平行;与另一个平面内的直线平行或异面.
思考2:平行于同一个平面的两个平面什么关系?
答案:平行.名师点津(1)已知两个平面平行,虽然一个平面内的任何直线都平行于另一个平面,但是这两个平面内的所有直线并不一定相互平行,它们可能是平行直线,也可能是异面
直线,但不可能是相交直线.
(2)该定理提供了证明线线平行的另一种方法,应用时要紧扣与两个平行平面都相交的第三个平面.课堂探究·素养提升题型一 面面平行性质定理的应用
[例1](2018·河南林州一中高一检测)如图所示,两条异面直线BA,DC与两平行平面α,β分别交于B,A和D,C,M,N分别是AB,CD的中点.求证:MN∥平面α.方法技巧(1)利用面面平行的性质定理判定两直线平行的步骤:
①先找两个平面,使这两个平面分别经过这两条直线中的一条;
②判定这两个平面平行;
③再找一个平面,使这两条直线都在这个平面上;
④由性质定理得出线线平行.
(2)应用面面平行的性质定理时,往往需要“作”或“找”辅助平面,但辅助平面不可乱作,要想办法与其他已知量联系起来.即时训练1-1:如图,在三棱柱ABC-A1B1C1中,M是A1C1的中点,平面AB1M∥平面BC1N,AC∩平面BC1N=N.求证:N为AC的中点. 题型二 平行关系的综合应用
[例2]如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AD∥BC,平面A1DCE与B1B交于点E.
求证:EC∥A1D. 证明:因为BE∥AA1,
AA1?平面AA1D,BE?平面AA1D,
所以BE∥平面AA1D.
因为BC∥AD,AD?平面AA1D,
BC?平面AA1D,所以BC∥平面AA1D.
又BE∩BC=B,
BE?平面BCE,BC?平面BCE,
所以平面BCE∥平面AA1D.
又平面A1DCE∩平面BCE=EC,
平面A1DCE∩平面AA1D=A1D,
所以EC∥A1D.方法技巧要灵活应用线线平行、线面平行和面面平行的相互联系、相互转化.在解决立体几何中的平行问题时,一般都要用到平行关系的转化.转化思想是解决这类问题的最有效的方法.具体转化过程如图所示:即时训练2-1:如图,正方体ABCD-A1B1C1D1,点E在AB1上,点F在BD上,且B1E=BF.求证:EF∥平面BB1C1C.所以ME∥BB1.
因为ME?平面BB1C1C,BB1?平面BB1C1C,
所以ME∥平面BB1C1C.
由FM∥AD,AD∥BC,知FM∥BC.
而FM?平面BB1C1C,BC?平面BB1C1C,
所以FM∥平面BB1C1C.
因为FM∩ME=M.
所以平面MEF∥平面BB1C1C.
因为EF?平面MEF,
所以EF∥平面BB1C1C.课堂达标1.已知平面α∥平面β,a?α,b?β,则直线a,b的位置关系是( )
(A)平行 (B)相交
(C)异面 (D)平行或异面D解析:因为平面α∥平面β,所以平面α与平面β没有公共点.因为a?α,b?β,所以直线a,b没有公共点,所以直线a,b的位置关系是平行或异面.2.若平面α∥平面β,直线a?α,点B∈β,过点B的所有直线中( )
(A)不一定存在与a平行的直线
(B)只有两条与a平行的直线
(C)存在无数条与a平行的直线
(D)有且只有一条与a平行的直线D3.过两平行平面α,β外的点P的两条直线AB与CD,它们分别交α于A,C两点,交β于B,D两点,若PA=6,AC=9,PB=8,则BD的长为 .?答案:124.如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为 .?解析:因为平面ABFE∥平面CDHG,
又平面EFGH∩平面ABFE=EF,
平面EFGH∩平面CDHG=HG,
所以EF∥HG.
同理EH∥FG,
所以四边形EFGH的形状是平行四边形.答案:平行四边形
