人教A版高中数学必修二 课件 2.3.3 直线与平面垂直的性质2.3.4 平面与平面垂直的性质 :36张PPT
文档属性
| 名称 | 人教A版高中数学必修二 课件 2.3.3 直线与平面垂直的性质2.3.4 平面与平面垂直的性质 :36张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 00:00:00 | ||
图片预览








文档简介
课件36张PPT。2.3.3 直线与平面垂直的性质
2.3.4 平面与平面垂直的性质目标导航新知导学·素养养成1.直线与平面垂直的性质定理a∥b平行2.平面与平面垂直的性质定理一个平面内交线垂直名师点津(1)对线面垂直定理的理解
①直线与平面垂直的性质定理给出了判定两条直线平行的另一种方法.
②定理揭示了空间中“平行”与“垂直”关系的内在联系,提供了“垂直”与“平行”关系转化的依据.
(2)对面面垂直的性质定理的理解
①定理的实质是由面面垂直得线面垂直,故可用来证明线面垂直.
②已知面面垂直时,可以利用此定理转化为线面垂直,再转化为线线 垂直.课堂探究·素养提升题型一 直线与平面垂直的性质定理的应用
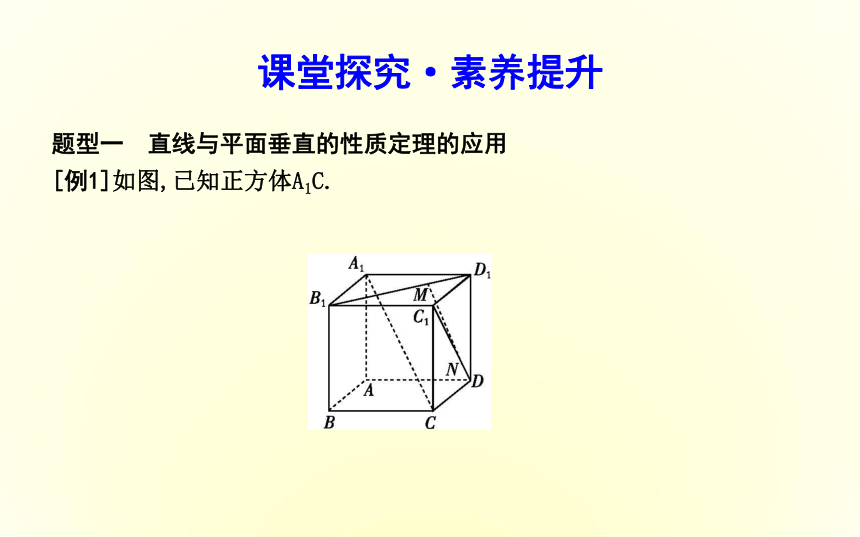
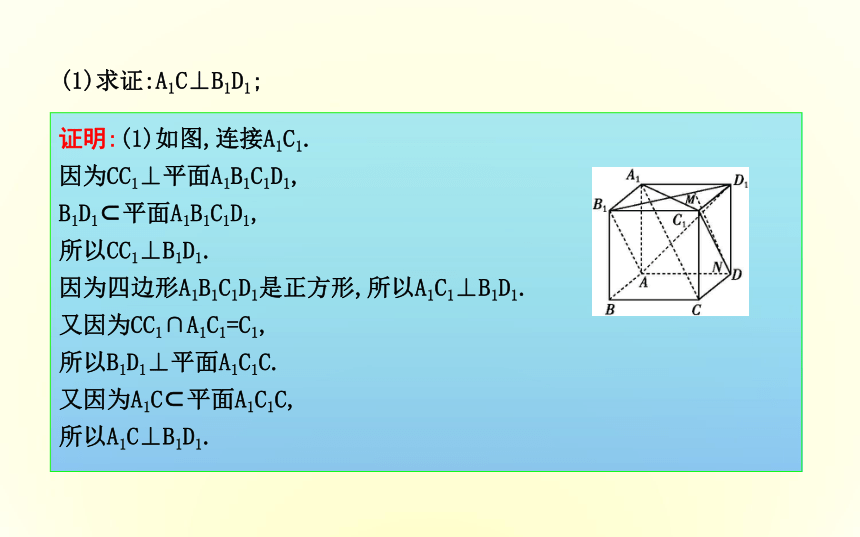
[例1]如图,已知正方体A1C.证明:(1)如图,连接A1C1.
因为CC1⊥平面A1B1C1D1,
B1D1?平面A1B1C1D1,
所以CC1⊥B1D1.
因为四边形A1B1C1D1是正方形,所以A1C1⊥B1D1.
又因为CC1∩A1C1=C1,
所以B1D1⊥平面A1C1C.
又因为A1C?平面A1C1C,
所以A1C⊥B1D1.(1)求证:A1C⊥B1D1;证明:(2)如图,连接B1A,AD1.
因为B1C1 AD,
所以四边形ADC1B1为平行四边形,
所以C1D∥AB1.
因为MN⊥C1D,所以MN⊥AB1.
又因为MN⊥B1D1,AB1∩B1D1=B1,
所以MN⊥平面AB1D1.
由(1)知A1C⊥B1D1.
同理可得A1C⊥AB1.
又因为AB1∩B1D1=B1,
所以A1C⊥平面AB1D1.所以MN∥A1C.(2)M,N分别为B1D1与C1D上的点,且MN⊥B1D1,MN⊥C1D,求证:MN∥A1C.方法技巧证明线线平行常有如下方法:
(1)利用线线平行定义:证共面且无公共点;
(2)利用三线平行公理:证两线同时平行于第三条直线;
(3)利用线面平行的性质定理:把证线线平行转化为证线面平行;
(4)利用线面垂直的性质定理:把证线线平行转化为证线面垂直;
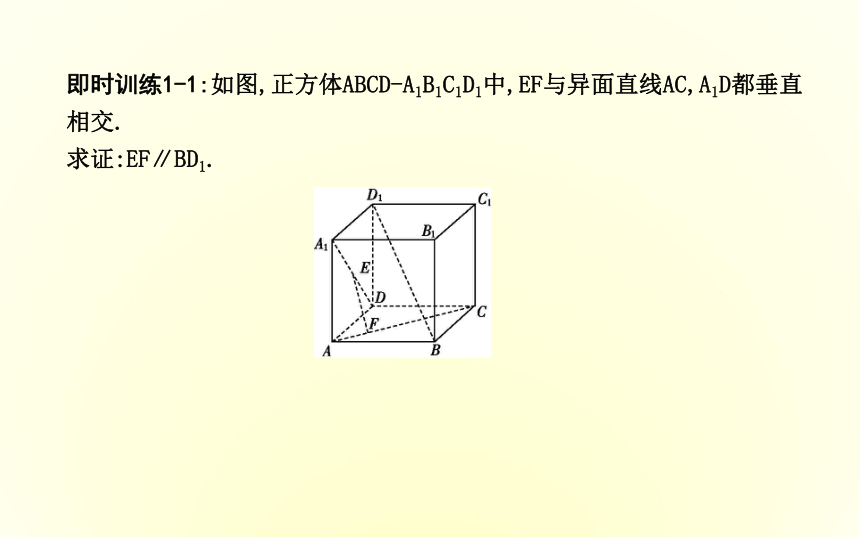
(5)利用面面平行的性质定理:把证线线平行转化为证面面平行.即时训练1-1:如图,正方体ABCD-A1B1C1D1中,EF与异面直线AC,A1D都垂直相交.
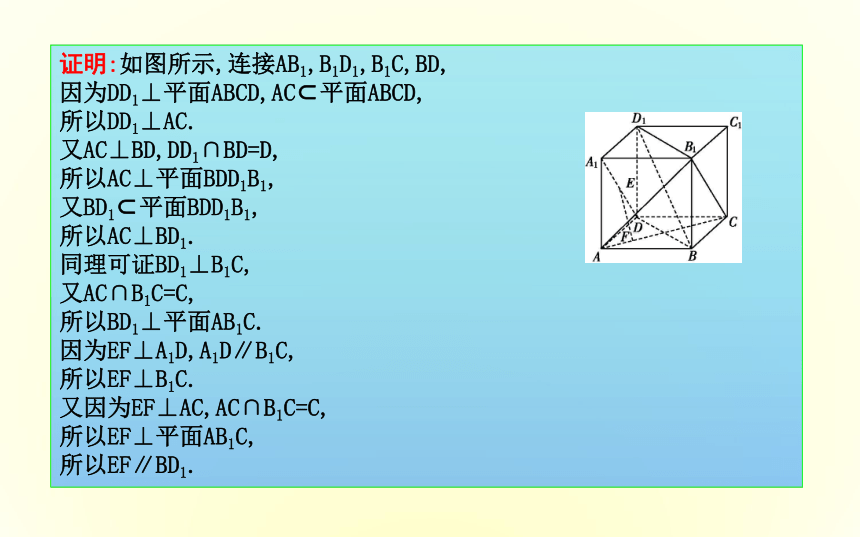
求证:EF∥BD1.证明:如图所示,连接AB1,B1D1,B1C,BD,
因为DD1⊥平面ABCD,AC?平面ABCD,
所以DD1⊥AC.
又AC⊥BD,DD1∩BD=D,
所以AC⊥平面BDD1B1,
又BD1?平面BDD1B1,
所以AC⊥BD1.
同理可证BD1⊥B1C,
又AC∩B1C=C,
所以BD1⊥平面AB1C.
因为EF⊥A1D,A1D∥B1C,
所以EF⊥B1C.
又因为EF⊥AC,AC∩B1C=C,
所以EF⊥平面AB1C,
所以EF∥BD1.[备用例1]如图,在四棱锥PABCD中,底面ABCD为菱形,PB⊥平面ABCD.
(1)若AC=6,BD=8,PB=3,求三棱锥A-PBC的体积;(2)若点E是DP的中点,证明:BD⊥平面ACE.(2)证明:如图,设BD与AC相交于点O,连接OE,
因为O为BD的中点,
E是DP的中点,
所以OE∥PB.
又PB⊥平面ABCD,
所以OE⊥平面ABCD.
因为BD?平面ABCD,
所以OE⊥BD,
由(1)知AC⊥BD,
又AC∩OE=O,
所以BD⊥平面ACE.题型二 平面与平面垂直的性质定理的应用
[例2](12分)如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°,且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD. [规范解答]证明:(1)连接PG,由题知△PAD为正三角形,G是AD的中点,则PG⊥AD.…………………………………………………………………1分
又因为平面PAD⊥平面ABCD,PG?平面PAD,
所以PG⊥平面ABCD. …………………………………………………3分
因为BG?平面ABCD,
所以PG⊥BG. …………………………………………………………4分
又因为四边形ABCD是菱形,且∠DAB=60°,
所以△ABD是正三角形.
则BG⊥AD. ……………………………………………………………6分
又因为AD∩PG=G,且AD,PG?平面PAD,所以BG⊥平面PAD. ………8分(1)若G为AD边的中点,求证:BG⊥平面PAD;(2)求证:AD⊥PB.[规范解答]证明:(2)由(1)可知BG⊥AD,PG⊥AD.
又BG∩PG=G,
所以AD⊥平面PBG. …………………………………………………10分
因为PB?平面PBG,
所以AD⊥PB. ………………………………………………………12分方法技巧证明线面垂直,一种方法是利用线面垂直的判定定理,另一种方法是利用面面垂直的性质定理,本题已知面面垂直,故可考虑面面垂直的性质定理.利用面面垂直的性质定理,证明线面垂直的问题时,要注意以下三点:
(1)两个平面垂直;
(2)直线必须在其中一个平面内;
(3)直线必须垂直于它们的交线.即时训练2-1:如图,四棱锥VABCD的底面是矩形,侧面VAB⊥底面ABCD,又VB⊥平面VAD.求证:平面VBC⊥平面VAC. 证明:因为平面VAB⊥底面ABCD,且BC⊥AB.
所以BC⊥平面VAB,
所以BC⊥VA,
又VB⊥平面VAD,
所以VB⊥VA,
又VB∩BC=B,
所以VA⊥平面VBC,
因为VA?平面VAC.
所以平面VBC⊥平面VAC.[备用例2]
如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形, AE=BE,平面ABCD⊥平面ABE,点F在CE上,且BF⊥平面ACE.
(1)求证:AE⊥平面BCE;(1)证明:因为BF⊥平面ACE,AE?平面ACE,所以BF⊥AE,
又因为平面ABCD⊥平面ABE,平面ABCD∩平面ABE=AB,BC⊥AB,
所以BC⊥平面ABE,
从而,BC⊥AE,且BC∩BF=B,
所以AE⊥平面BCE.(2)求点D到平面ACE的距离.(1)求证:EO∥平面PCD;(2)求证:CD⊥平面PAC;(2)证明:因为平面PAB⊥平面ABCD,PA⊥AB,平面PAB∩平面ABCD=AB,
所以PA⊥平面ABCD,
因为CD?平面ABCD,
所以PA⊥CD,
因为AC⊥CD,AC∩PA=A,
所以CD⊥平面PAC.(3)在线段PD上是否存在点F,使得CF⊥AD,并说明理由.(3)解:在线段PD上存在点F,使得CF⊥AD.
理由如下:
过C作CG⊥AD,交AD于G,作GF⊥AD,
交PD于F,连接CF,
因为CG⊥AD,GF⊥AD,CG∩GF=G,
所以AD⊥平面CFG,
所以AD⊥CF,
故在线段PD上存在点F,使得CF⊥AD.方法技巧(2)空间问题化成平面问题是解决立体几何问题的一个基本原则,解题时,要抓住几何图形自身的特点,如等腰(边)三角形的三线合一、中位线定理、菱形的对角线互相垂直等.还可以通过解三角形,产生一些题目所需要的条件,对于一些较复杂的问题,注意应用转化思想解决问题.即时训练3-1:已知:如图,平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,E为垂足.
(1)求证:PA⊥平面ABC;证明:(1)在平面ABC内任取一点D,作DF⊥AC于点F,作DG⊥AB于点G.
因为平面PAC⊥平面ABC,且交线为AC,
所以DF⊥平面PAC.
因为PA?平面PAC,
所以DF⊥PA.
同理可证,DG⊥PA.
因为DG∩DF=D,
所以PA⊥平面ABC.(2)当E为△PBC的垂心时,求证:△ABC是直角三角形.证明:(2)连接BE并延长交PC于点H.
因为E是△PBC的垂心,
所以PC⊥BH.
又因为AE是平面PBC的垂线,
所以PC⊥AE.
因为BH∩AE=E,
所以PC⊥平面ABE,
所以PC⊥AB.
又因为PA⊥平面ABC,
所以PA⊥AB.
因为PA∩PC=P,
所以AB⊥平面PAC.
所以AB⊥AC,
即△ABC是直角三角形.[备用例3]
如图,在矩形ABCD中,AB=2AD,E是AB的中点,沿DE将△ADE折起.(1)如果二面角A-DE-C是直二面角,求证:AB=AC;证明:(1)过点A作AM⊥DE于点M,则AM⊥平面BCDE,
所以AM⊥BC.
又AD=AE,
所以M是DE的中点.取BC的中点N,
连接MN,AN,则MN⊥BC.
又AM⊥BC,AM∩MN=M,
所以BC⊥平面AMN,
所以AN⊥BC.
又因为N是BC的中点,
所以AB=AC.(2)如果AB=AC,求证:平面ADE⊥平面BCDE.证明:(2)取BC的中点N,连接AN.
因为AB=AC,所以AN⊥BC.
取DE的中点M,连接MN,AM,
所以MN⊥BC.又AN∩MN=N,
所以BC⊥平面AMN,
所以AM⊥BC.
又M是DE的中点,AD=AE,
所以AM⊥DE.
又因为DE与BC是平面BCDE内的相交直线,
所以AM⊥平面BCDE.因为AM?平面ADE,
所以平面ADE⊥平面BCDE.课堂达标1.若a,b表示直线,α表示平面,下列命题中正确的个数为( )
①a⊥α,b∥α?a⊥b;②a⊥α,a⊥b?b∥α;③a∥α,a⊥b?b⊥α;④a⊥α,b⊥α?a∥b.
(A)1 (B)2 (C)3 (D)0B解析:由线面垂直的性质知①④正确.②中b可能满足b?α,故②错误;③中b可能与α相交(不垂直),也可能平行,也可能b?α,故③不正确.故选B.2.△ABC所在的平面为α,直线l⊥AB,l⊥AC,直线m⊥BC,m⊥AC,则直线l,m的位置关系是( )
(A)相交 (B)异面
(C)平行 (D)不确定C解析:因为l⊥AB,l⊥AC,AB?α,AC?α且AB∩AC=A,所以l⊥α,同理可证m⊥α,所以l∥m.故选C.3.若平面α⊥平面β,且平面α内的一条直线a垂直于平面β内的一条直线b,则( )
(A)直线a必垂直于平面β
(B)直线b必垂直于平面α
(C)直线a不一定垂直于平面β
(D)过a的平面与过b的平面垂直C解析:α⊥β,a?α,b?β,a⊥b,当α∩β=a时,b⊥α;当α∩β=b时,a⊥β,其他情形则未必有b⊥α或a⊥β,所以选项A,B,D都错误,故选C.4.已知AF⊥平面ABCD,DE⊥平面ABCD,如图所示,且AF=DE,AD=6,则EF= .?解析:因为AF⊥平面ABCD,DE⊥平面ABCD,所以AF∥DE,又AF=DE,所以四边形AFED是平行四边形,所以EF=AD=6.
答案:65.如图,在三棱锥P-ABC内,侧面PAC⊥底面ABC,且∠PAC=90°,PA=1, AB=2,则PB= .
2.3.4 平面与平面垂直的性质目标导航新知导学·素养养成1.直线与平面垂直的性质定理a∥b平行2.平面与平面垂直的性质定理一个平面内交线垂直名师点津(1)对线面垂直定理的理解
①直线与平面垂直的性质定理给出了判定两条直线平行的另一种方法.
②定理揭示了空间中“平行”与“垂直”关系的内在联系,提供了“垂直”与“平行”关系转化的依据.
(2)对面面垂直的性质定理的理解
①定理的实质是由面面垂直得线面垂直,故可用来证明线面垂直.
②已知面面垂直时,可以利用此定理转化为线面垂直,再转化为线线 垂直.课堂探究·素养提升题型一 直线与平面垂直的性质定理的应用
[例1]如图,已知正方体A1C.证明:(1)如图,连接A1C1.
因为CC1⊥平面A1B1C1D1,
B1D1?平面A1B1C1D1,
所以CC1⊥B1D1.
因为四边形A1B1C1D1是正方形,所以A1C1⊥B1D1.
又因为CC1∩A1C1=C1,
所以B1D1⊥平面A1C1C.
又因为A1C?平面A1C1C,
所以A1C⊥B1D1.(1)求证:A1C⊥B1D1;证明:(2)如图,连接B1A,AD1.
因为B1C1 AD,
所以四边形ADC1B1为平行四边形,
所以C1D∥AB1.
因为MN⊥C1D,所以MN⊥AB1.
又因为MN⊥B1D1,AB1∩B1D1=B1,
所以MN⊥平面AB1D1.
由(1)知A1C⊥B1D1.
同理可得A1C⊥AB1.
又因为AB1∩B1D1=B1,
所以A1C⊥平面AB1D1.所以MN∥A1C.(2)M,N分别为B1D1与C1D上的点,且MN⊥B1D1,MN⊥C1D,求证:MN∥A1C.方法技巧证明线线平行常有如下方法:
(1)利用线线平行定义:证共面且无公共点;
(2)利用三线平行公理:证两线同时平行于第三条直线;
(3)利用线面平行的性质定理:把证线线平行转化为证线面平行;
(4)利用线面垂直的性质定理:把证线线平行转化为证线面垂直;
(5)利用面面平行的性质定理:把证线线平行转化为证面面平行.即时训练1-1:如图,正方体ABCD-A1B1C1D1中,EF与异面直线AC,A1D都垂直相交.
求证:EF∥BD1.证明:如图所示,连接AB1,B1D1,B1C,BD,
因为DD1⊥平面ABCD,AC?平面ABCD,
所以DD1⊥AC.
又AC⊥BD,DD1∩BD=D,
所以AC⊥平面BDD1B1,
又BD1?平面BDD1B1,
所以AC⊥BD1.
同理可证BD1⊥B1C,
又AC∩B1C=C,
所以BD1⊥平面AB1C.
因为EF⊥A1D,A1D∥B1C,
所以EF⊥B1C.
又因为EF⊥AC,AC∩B1C=C,
所以EF⊥平面AB1C,
所以EF∥BD1.[备用例1]如图,在四棱锥PABCD中,底面ABCD为菱形,PB⊥平面ABCD.
(1)若AC=6,BD=8,PB=3,求三棱锥A-PBC的体积;(2)若点E是DP的中点,证明:BD⊥平面ACE.(2)证明:如图,设BD与AC相交于点O,连接OE,
因为O为BD的中点,
E是DP的中点,
所以OE∥PB.
又PB⊥平面ABCD,
所以OE⊥平面ABCD.
因为BD?平面ABCD,
所以OE⊥BD,
由(1)知AC⊥BD,
又AC∩OE=O,
所以BD⊥平面ACE.题型二 平面与平面垂直的性质定理的应用
[例2](12分)如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°,且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD. [规范解答]证明:(1)连接PG,由题知△PAD为正三角形,G是AD的中点,则PG⊥AD.…………………………………………………………………1分
又因为平面PAD⊥平面ABCD,PG?平面PAD,
所以PG⊥平面ABCD. …………………………………………………3分
因为BG?平面ABCD,
所以PG⊥BG. …………………………………………………………4分
又因为四边形ABCD是菱形,且∠DAB=60°,
所以△ABD是正三角形.
则BG⊥AD. ……………………………………………………………6分
又因为AD∩PG=G,且AD,PG?平面PAD,所以BG⊥平面PAD. ………8分(1)若G为AD边的中点,求证:BG⊥平面PAD;(2)求证:AD⊥PB.[规范解答]证明:(2)由(1)可知BG⊥AD,PG⊥AD.
又BG∩PG=G,
所以AD⊥平面PBG. …………………………………………………10分
因为PB?平面PBG,
所以AD⊥PB. ………………………………………………………12分方法技巧证明线面垂直,一种方法是利用线面垂直的判定定理,另一种方法是利用面面垂直的性质定理,本题已知面面垂直,故可考虑面面垂直的性质定理.利用面面垂直的性质定理,证明线面垂直的问题时,要注意以下三点:
(1)两个平面垂直;
(2)直线必须在其中一个平面内;
(3)直线必须垂直于它们的交线.即时训练2-1:如图,四棱锥VABCD的底面是矩形,侧面VAB⊥底面ABCD,又VB⊥平面VAD.求证:平面VBC⊥平面VAC. 证明:因为平面VAB⊥底面ABCD,且BC⊥AB.
所以BC⊥平面VAB,
所以BC⊥VA,
又VB⊥平面VAD,
所以VB⊥VA,
又VB∩BC=B,
所以VA⊥平面VBC,
因为VA?平面VAC.
所以平面VBC⊥平面VAC.[备用例2]
如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形, AE=BE,平面ABCD⊥平面ABE,点F在CE上,且BF⊥平面ACE.
(1)求证:AE⊥平面BCE;(1)证明:因为BF⊥平面ACE,AE?平面ACE,所以BF⊥AE,
又因为平面ABCD⊥平面ABE,平面ABCD∩平面ABE=AB,BC⊥AB,
所以BC⊥平面ABE,
从而,BC⊥AE,且BC∩BF=B,
所以AE⊥平面BCE.(2)求点D到平面ACE的距离.(1)求证:EO∥平面PCD;(2)求证:CD⊥平面PAC;(2)证明:因为平面PAB⊥平面ABCD,PA⊥AB,平面PAB∩平面ABCD=AB,
所以PA⊥平面ABCD,
因为CD?平面ABCD,
所以PA⊥CD,
因为AC⊥CD,AC∩PA=A,
所以CD⊥平面PAC.(3)在线段PD上是否存在点F,使得CF⊥AD,并说明理由.(3)解:在线段PD上存在点F,使得CF⊥AD.
理由如下:
过C作CG⊥AD,交AD于G,作GF⊥AD,
交PD于F,连接CF,
因为CG⊥AD,GF⊥AD,CG∩GF=G,
所以AD⊥平面CFG,
所以AD⊥CF,
故在线段PD上存在点F,使得CF⊥AD.方法技巧(2)空间问题化成平面问题是解决立体几何问题的一个基本原则,解题时,要抓住几何图形自身的特点,如等腰(边)三角形的三线合一、中位线定理、菱形的对角线互相垂直等.还可以通过解三角形,产生一些题目所需要的条件,对于一些较复杂的问题,注意应用转化思想解决问题.即时训练3-1:已知:如图,平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,E为垂足.
(1)求证:PA⊥平面ABC;证明:(1)在平面ABC内任取一点D,作DF⊥AC于点F,作DG⊥AB于点G.
因为平面PAC⊥平面ABC,且交线为AC,
所以DF⊥平面PAC.
因为PA?平面PAC,
所以DF⊥PA.
同理可证,DG⊥PA.
因为DG∩DF=D,
所以PA⊥平面ABC.(2)当E为△PBC的垂心时,求证:△ABC是直角三角形.证明:(2)连接BE并延长交PC于点H.
因为E是△PBC的垂心,
所以PC⊥BH.
又因为AE是平面PBC的垂线,
所以PC⊥AE.
因为BH∩AE=E,
所以PC⊥平面ABE,
所以PC⊥AB.
又因为PA⊥平面ABC,
所以PA⊥AB.
因为PA∩PC=P,
所以AB⊥平面PAC.
所以AB⊥AC,
即△ABC是直角三角形.[备用例3]
如图,在矩形ABCD中,AB=2AD,E是AB的中点,沿DE将△ADE折起.(1)如果二面角A-DE-C是直二面角,求证:AB=AC;证明:(1)过点A作AM⊥DE于点M,则AM⊥平面BCDE,
所以AM⊥BC.
又AD=AE,
所以M是DE的中点.取BC的中点N,
连接MN,AN,则MN⊥BC.
又AM⊥BC,AM∩MN=M,
所以BC⊥平面AMN,
所以AN⊥BC.
又因为N是BC的中点,
所以AB=AC.(2)如果AB=AC,求证:平面ADE⊥平面BCDE.证明:(2)取BC的中点N,连接AN.
因为AB=AC,所以AN⊥BC.
取DE的中点M,连接MN,AM,
所以MN⊥BC.又AN∩MN=N,
所以BC⊥平面AMN,
所以AM⊥BC.
又M是DE的中点,AD=AE,
所以AM⊥DE.
又因为DE与BC是平面BCDE内的相交直线,
所以AM⊥平面BCDE.因为AM?平面ADE,
所以平面ADE⊥平面BCDE.课堂达标1.若a,b表示直线,α表示平面,下列命题中正确的个数为( )
①a⊥α,b∥α?a⊥b;②a⊥α,a⊥b?b∥α;③a∥α,a⊥b?b⊥α;④a⊥α,b⊥α?a∥b.
(A)1 (B)2 (C)3 (D)0B解析:由线面垂直的性质知①④正确.②中b可能满足b?α,故②错误;③中b可能与α相交(不垂直),也可能平行,也可能b?α,故③不正确.故选B.2.△ABC所在的平面为α,直线l⊥AB,l⊥AC,直线m⊥BC,m⊥AC,则直线l,m的位置关系是( )
(A)相交 (B)异面
(C)平行 (D)不确定C解析:因为l⊥AB,l⊥AC,AB?α,AC?α且AB∩AC=A,所以l⊥α,同理可证m⊥α,所以l∥m.故选C.3.若平面α⊥平面β,且平面α内的一条直线a垂直于平面β内的一条直线b,则( )
(A)直线a必垂直于平面β
(B)直线b必垂直于平面α
(C)直线a不一定垂直于平面β
(D)过a的平面与过b的平面垂直C解析:α⊥β,a?α,b?β,a⊥b,当α∩β=a时,b⊥α;当α∩β=b时,a⊥β,其他情形则未必有b⊥α或a⊥β,所以选项A,B,D都错误,故选C.4.已知AF⊥平面ABCD,DE⊥平面ABCD,如图所示,且AF=DE,AD=6,则EF= .?解析:因为AF⊥平面ABCD,DE⊥平面ABCD,所以AF∥DE,又AF=DE,所以四边形AFED是平行四边形,所以EF=AD=6.
答案:65.如图,在三棱锥P-ABC内,侧面PAC⊥底面ABC,且∠PAC=90°,PA=1, AB=2,则PB= .
