人教A版高中数学必修二 课件 2章末总结 :39张PPT
文档属性
| 名称 | 人教A版高中数学必修二 课件 2章末总结 :39张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 21:37:54 | ||
图片预览







文档简介
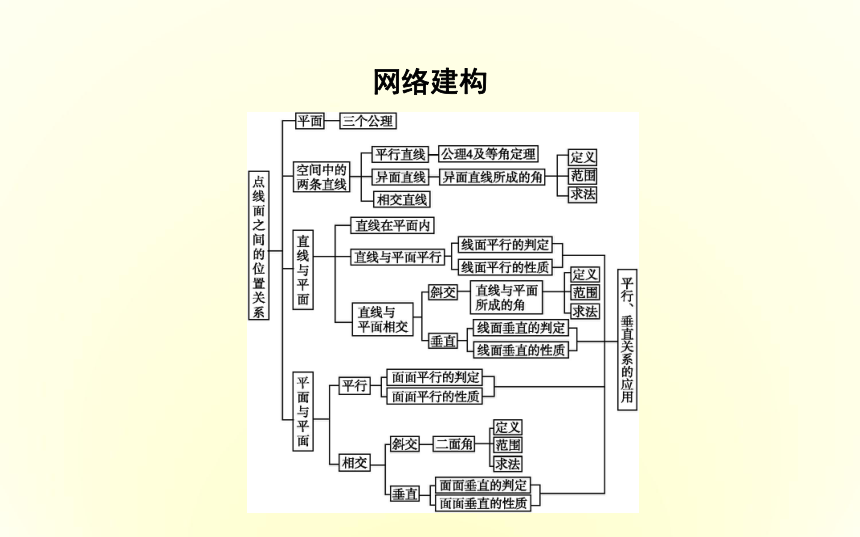
课件39张PPT。章末总结网络建构知识辨析判断下列说法是否正确(请在括号中填“√”或“×”)
1.如果一条直线过平面内一点与平面外一点,那么这条直线与这个平面有且只有一个交点.( )√2.如果两个平面有一个交点,则这两个平面有一条过这个点的公共直线.( )
3.如果两个平面平行,则这两个平面没有交点.( )
4.若一条直线上有两个点在某一平面内,则这条直线上有无数个点在这个平面内.( )
5.平行于同一条直线的两个平面平行.( )√√√×6.一条直线垂直于一个平面内的三条直线,则这条直线垂直于这个平面.( )×7.两个相交平面组成的图形叫做二面角.( )
8.垂直于同一条直线的两个平面平行.( )×√题型探究真题赏析题型探究·素养提升题型一 平面基本性质的应用
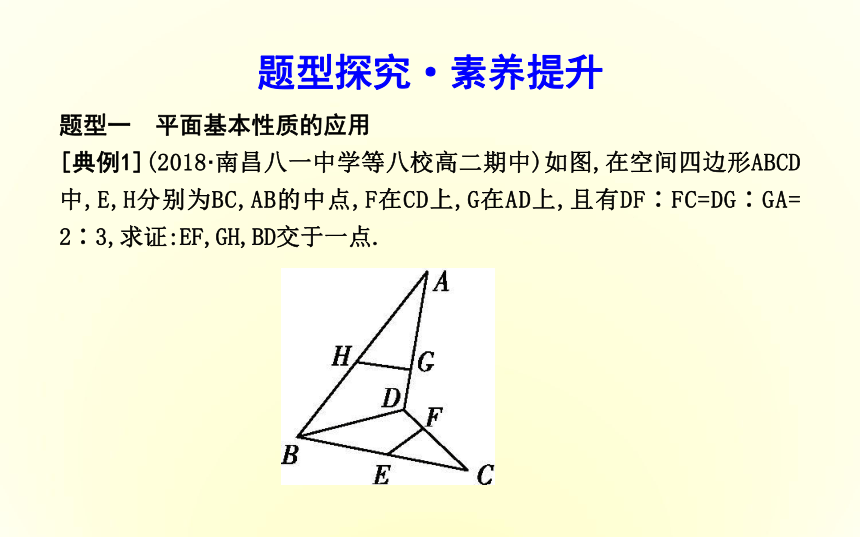
[典例1](2018·南昌八一中学等八校高二期中)如图,在空间四边形ABCD中,E,H分别为BC,AB的中点,F在CD上,G在AD上,且有DF∶FC=DG∶GA=
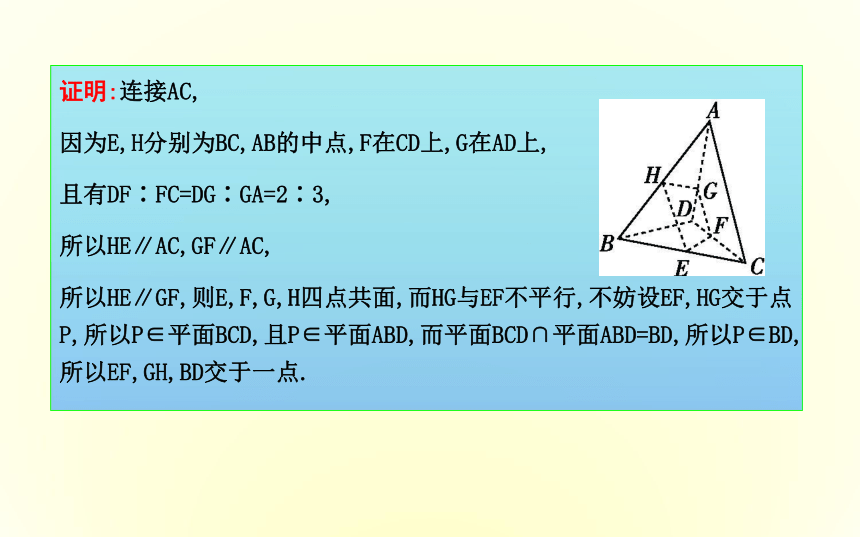
2∶3,求证:EF,GH,BD交于一点.证明:连接AC,
因为E,H分别为BC,AB的中点,F在CD上,G在AD上,
且有DF∶FC=DG∶GA=2∶3,
所以HE∥AC,GF∥AC,
所以HE∥GF,则E,F,G,H四点共面,而HG与EF不平行,不妨设EF,HG交于点P,所以P∈平面BCD,且P∈平面ABD,而平面BCD∩平面ABD=BD,所以P∈BD,所以EF,GH,BD交于一点.规律方法(1)证明共面问题
证明共面问题,一般有两种证法:一是由某些元素确定一个平面,再证明其余元素在这个平面内;二是分别由不同元素确定若干个平面,再证明这些平面重合.
(2)证明三点共线问题
证明空间三点共线问题,通常证明这些点都在两个面的交线上,即先确定出某两点在某两个平面的交线上,再证明第三个点是两个平面的公共点,当然必在两个平面的交线上.
(3)证明三线共点问题
证明空间三线共点问题,先证两条直线交于一点,再证明第三条直线经过这点,把问题转化为证明点在直线上的问题.题型二 空间中的平行关系
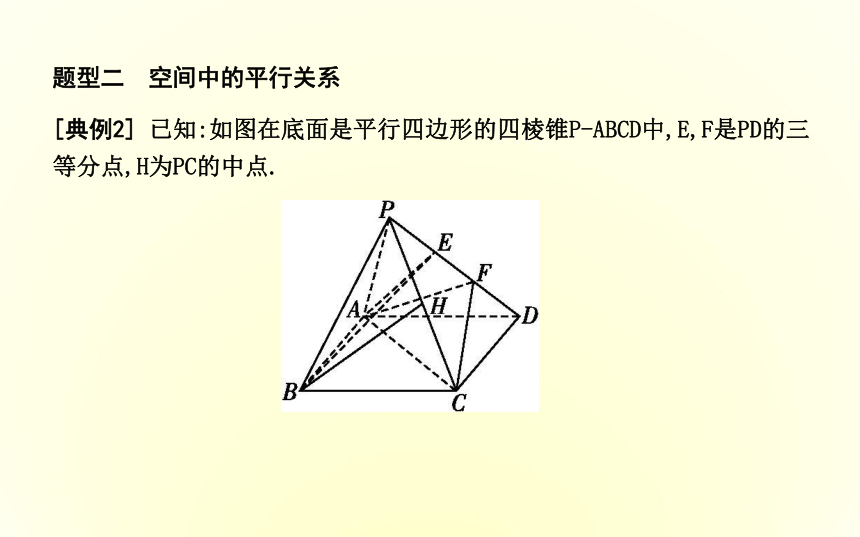
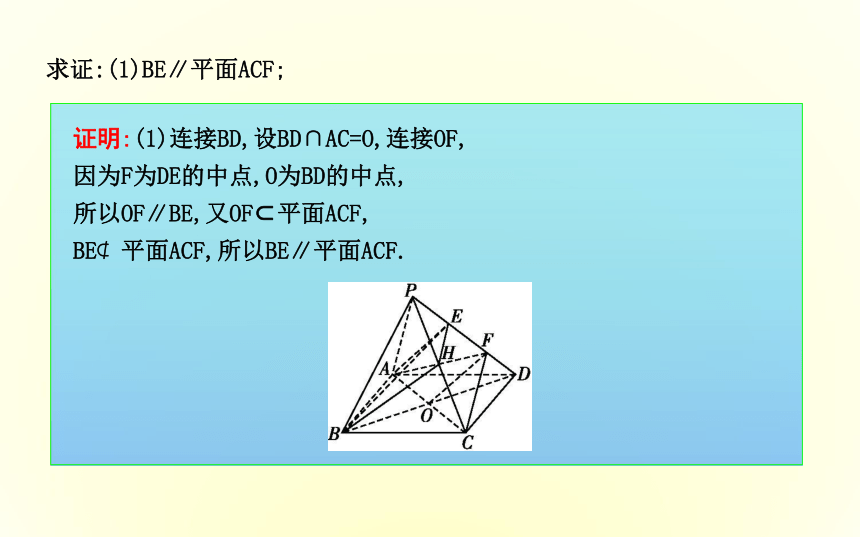
[典例2] 已知:如图在底面是平行四边形的四棱锥P-ABCD中,E,F是PD的三等分点,H为PC的中点.求证:(1)BE∥平面ACF;证明:(1)连接BD,设BD∩AC=O,连接OF,
因为F为DE的中点,O为BD的中点,
所以OF∥BE,又OF?平面ACF,
BE?平面ACF,所以BE∥平面ACF.(2)BH∥平面ACF.证明:(2)连接HE,因为E为PF的中点,H为PC的中点,
所以EH∥FC,因为FC?平面ACF,HE?平面ACF,
所以HE∥平面ACF,
又BE∥平面ACF,
BE?平面BHE,HE?平面BHE且BE∩HE=E,
所以平面BHE∥平面ACF,
又BH?平面BHE,故BH∥平面ACF.规律方法(1)判断线面平行的两种方法
面面平行的落脚点是线面平行,因此掌握线面平行的判定方法是必要的,判定线面平行的两种方法:①利用线面平行的判定定理;②利用面面平行的性质,即当两平面平行时,其中一平面内的任一直线平行于另一个平面.
(2)判断面面平行的常用方法
①利用面面平行的判定定理,
②面面平行的传递性(α∥β,β∥γ?α∥γ),
③利用线面垂直的性质(l⊥α,l⊥β?α∥β)(1)求证:BD⊥A1C;(2)求证:AB1⊥平面A1BC.证明:(2)由(1)知AB=BC,AB⊥BC,
因为BB1=BC,所以四边形ABB1A1是菱形,所以AB1⊥A1B,
因为BB1⊥平面ABC,BC?平面ABC.所以BC⊥BB1
因为AB∩BB1=B,AB,BB1?平面ABB1A1.
所以BC⊥平面ABB1A1.
因为AB1?平面ABB1A1,
所以BC⊥AB1,
因为BC∩A1B=B,BC,A1B?平面A1BC,
所以AB1⊥平面A1BC.规律方法空间垂直关系的判定方法
(1)判定线线垂直的方法:
①计算所成的角为90°(包括平面角和异面直线所成的角);
②线面垂直的性质(若a⊥α,b?α,则a⊥b).
(2)判定线面垂直的方法:
①线面垂直定义(一般不易验证任意性);
②线面垂直的判定定理(a⊥b,a⊥c,b?α,c?α,b∩c=M?a⊥α);③平行线垂直平面的传递性质(a∥b,b⊥α?a⊥α);
④面面垂直的性质(α⊥β,α∩β=l,a?β,a⊥l?a⊥α);
⑤面面平行的性质(a⊥α,α∥β?a⊥β);
⑥面面垂直的性质(α∩β=l,α⊥γ,β⊥γ?l⊥γ).
(3)面面垂直的判定方法:
①根据定义(作两平面构成二面角的平面角,计算其为90°);
②面面垂直的判定定理(a⊥β,a?α?α⊥β).题型四 空间角问题
[典例4] (2017·天津卷)如图,在四棱锥P-ABCD中,AD⊥平面PDC,AD∥BC,
PD⊥PB,AD=1,BC=3,CD=4,PD=2.(1)求异面直线AP与BC所成角的余弦值;(2)求证:PD⊥平面PBC;(2)证明:由(1)知AD⊥PD.
又因为BC∥AD,所以PD⊥BC.
又PD⊥PB,PB∩BC=B,所以PD⊥平面PBC.(3)求直线AB与平面PBC所成角的正弦值.规律方法求角度问题时,无论哪种情况最终都归结到两条相交直线所成的角的问题上,求角度的解题步骤是:(1)找出这个角;(2)证该角符合题意;(3)构造出含这个角的三角形,解这个三角形,求出角.空间角包括以下三类:
①两条异面直线所成的角,找两条异面直线所成的角,关键是选取合适的点引两条异面直线的平行线,这两条相交直线所成的锐角或直角即为两条异面直线所成的角.
②求直线与平面所成的角关键是确定斜线在平面内的射影.
③求二面角关键是作出二面角的平面角,而作二面角的平面角时,首先要确定二面角的棱,然后结合题设构造二面角的平面角.题型五 空间几何体中的体积计算
[典例5] (2018·合肥期末)如图所示,在直角梯形BCEF中,∠CBF=∠BCE=
90°,A,D分别是BF,CE上的点,AD∥BC,且DE=2AF=2AD(如图1).将四边形ADEF沿AD折起,使点E到达点G的位置,连接BG,BF,CG(如图2),且AB⊥GD.(1)证明:AC∥平面BFG;(2)当AB=DG=2,求三棱锥A-BCG的体积.规律方法(1)求空间几何体的体积的关键是确定几何体的高,若几何体的高容易求出,可直接代入体积公式计算,否则可用下列方法进行转化:
①等体积转化法:对于三棱锥因为任何一个面都可作为底面,所以在求三棱锥的体积时,可将其转化为底面积和高都易求的形式求解.
②补体法:将几何体补成易求体积的几何体,再根据它们的体积关系求解.
③分割法:将几何体分割为易求体积的几部分,分别求解再求和.
(2)有关平面图形翻折成空间图形的问题,应注意翻折前后各元素(直线、线段、角)的相对位置(平行、垂直)和数量的变化,搞清楚哪些发生了变化、哪些不变.题型六 易错辨析
[典例6] 如图,已知E,F分别是正方体ABCD-A1B1C1D1的棱AA1,CC1上的点,且AE=C1F.求证:四边形EBFD1是平行四边形.错解:因为平面A1ADD1∥平面B1BCC1,D1E=平面A1ADD1∩平面BFD1E,BF=平面B1BCC1∩平面BFD1E,所以D1E∥FB.同理可得D1F∥EB.
所以四边形EBFD1是平行四边形.
纠错:错解中盲目地认为E,B,F,D1四点共面,由已知条件并不能说明这四点共面,同时条件AE=C1F也没有用到.真题赏析·素养升级1.(2017·全国Ⅲ卷,文10)在正方体ABCD-A1B1C1D1中,E为棱CD的中点,则( )
(A)A1E⊥DC1 (B)A1E⊥BD
(C)A1E⊥BC1 (D)A1E⊥AC解析:如图,由题意可知
A1E?平面A1B1CD,
可以证明BC1⊥平面A1B1CD,
所以A1E⊥BC1,
故选C.C2.(2017·全国Ⅱ卷,理10)已知直三棱柱ABC-A1B1C1中,∠ABC=120°,AB=2,
BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为( )C解析:①可能有m⊥β,即α∥β,得①错,②③④正确.
答案:②③④3.(2016·全国Ⅱ卷,理14)α,β是两个平面,m,n是两条直线,有下列四个命题:
①如果m⊥n,m⊥α,n∥β,那么α⊥β.
②如果m⊥α,n∥α,那么m⊥n.
③如果α∥β,m?α,那么m∥β.
④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.
其中正确的命题有 .(填写所有正确命题的编号)?证明:(1)在平行六面体ABCD-A1B1C1D1中,
AB∥A1B1.
因为AB?平面A1B1C,A1B1?平面A1B1C,
所以AB∥平面A1B1C.4.(2018·江苏卷,15)在平行六面体ABCD-A1B1C1D1中,AA1=AB,AB1⊥B1C1.
求证:(1)AB∥平面A1B1C;证明:(2)在平行六面体ABCD-A1B1C1D1中,四边形ABB1A1为平行四边形.
又因为AA1=AB,所以四边形ABB1A1为菱形,
因此AB1⊥A1B.
又因为AB1⊥B1C1,BC∥B1C1,
所以AB1⊥BC.
又因为A1B∩BC=B,
A1B?平面A1BC,BC?平面A1BC,
所以AB1⊥平面A1BC.
因为AB1?平面ABB1A1,
所以平面ABB1A1⊥平面A1BC.(2)平面ABB1A1⊥平面A1BC.(1)证明:由已知可得,∠BAC=90°,
即BA⊥AC.
又BA⊥AD,AC∩AD=A.
所以AB⊥平面ACD.
又AB?平面ABC,
所以平面ACD⊥平面ABC.5.(2018·全国Ⅰ卷,文18)如图,在平行四边形ABCM中,AB=AC=3,∠ACM=
90°.以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.
(1)证明:平面ACD⊥平面ABC;(1)证明:由已知∠BAP=∠CDP=90°,得AB⊥AP,CD⊥PD.
由于AB∥CD,故AB⊥PD,又AP∩PD=P,
从而AB⊥平面PAD.
又AB?平面PAB,
所以平面PAB⊥平面PAD.6.(2017·全国Ⅰ卷,文18)如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=
∠CDP=90°.
(1)证明:平面PAB⊥平面PAD;
1.如果一条直线过平面内一点与平面外一点,那么这条直线与这个平面有且只有一个交点.( )√2.如果两个平面有一个交点,则这两个平面有一条过这个点的公共直线.( )
3.如果两个平面平行,则这两个平面没有交点.( )
4.若一条直线上有两个点在某一平面内,则这条直线上有无数个点在这个平面内.( )
5.平行于同一条直线的两个平面平行.( )√√√×6.一条直线垂直于一个平面内的三条直线,则这条直线垂直于这个平面.( )×7.两个相交平面组成的图形叫做二面角.( )
8.垂直于同一条直线的两个平面平行.( )×√题型探究真题赏析题型探究·素养提升题型一 平面基本性质的应用
[典例1](2018·南昌八一中学等八校高二期中)如图,在空间四边形ABCD中,E,H分别为BC,AB的中点,F在CD上,G在AD上,且有DF∶FC=DG∶GA=
2∶3,求证:EF,GH,BD交于一点.证明:连接AC,
因为E,H分别为BC,AB的中点,F在CD上,G在AD上,
且有DF∶FC=DG∶GA=2∶3,
所以HE∥AC,GF∥AC,
所以HE∥GF,则E,F,G,H四点共面,而HG与EF不平行,不妨设EF,HG交于点P,所以P∈平面BCD,且P∈平面ABD,而平面BCD∩平面ABD=BD,所以P∈BD,所以EF,GH,BD交于一点.规律方法(1)证明共面问题
证明共面问题,一般有两种证法:一是由某些元素确定一个平面,再证明其余元素在这个平面内;二是分别由不同元素确定若干个平面,再证明这些平面重合.
(2)证明三点共线问题
证明空间三点共线问题,通常证明这些点都在两个面的交线上,即先确定出某两点在某两个平面的交线上,再证明第三个点是两个平面的公共点,当然必在两个平面的交线上.
(3)证明三线共点问题
证明空间三线共点问题,先证两条直线交于一点,再证明第三条直线经过这点,把问题转化为证明点在直线上的问题.题型二 空间中的平行关系
[典例2] 已知:如图在底面是平行四边形的四棱锥P-ABCD中,E,F是PD的三等分点,H为PC的中点.求证:(1)BE∥平面ACF;证明:(1)连接BD,设BD∩AC=O,连接OF,
因为F为DE的中点,O为BD的中点,
所以OF∥BE,又OF?平面ACF,
BE?平面ACF,所以BE∥平面ACF.(2)BH∥平面ACF.证明:(2)连接HE,因为E为PF的中点,H为PC的中点,
所以EH∥FC,因为FC?平面ACF,HE?平面ACF,
所以HE∥平面ACF,
又BE∥平面ACF,
BE?平面BHE,HE?平面BHE且BE∩HE=E,
所以平面BHE∥平面ACF,
又BH?平面BHE,故BH∥平面ACF.规律方法(1)判断线面平行的两种方法
面面平行的落脚点是线面平行,因此掌握线面平行的判定方法是必要的,判定线面平行的两种方法:①利用线面平行的判定定理;②利用面面平行的性质,即当两平面平行时,其中一平面内的任一直线平行于另一个平面.
(2)判断面面平行的常用方法
①利用面面平行的判定定理,
②面面平行的传递性(α∥β,β∥γ?α∥γ),
③利用线面垂直的性质(l⊥α,l⊥β?α∥β)(1)求证:BD⊥A1C;(2)求证:AB1⊥平面A1BC.证明:(2)由(1)知AB=BC,AB⊥BC,
因为BB1=BC,所以四边形ABB1A1是菱形,所以AB1⊥A1B,
因为BB1⊥平面ABC,BC?平面ABC.所以BC⊥BB1
因为AB∩BB1=B,AB,BB1?平面ABB1A1.
所以BC⊥平面ABB1A1.
因为AB1?平面ABB1A1,
所以BC⊥AB1,
因为BC∩A1B=B,BC,A1B?平面A1BC,
所以AB1⊥平面A1BC.规律方法空间垂直关系的判定方法
(1)判定线线垂直的方法:
①计算所成的角为90°(包括平面角和异面直线所成的角);
②线面垂直的性质(若a⊥α,b?α,则a⊥b).
(2)判定线面垂直的方法:
①线面垂直定义(一般不易验证任意性);
②线面垂直的判定定理(a⊥b,a⊥c,b?α,c?α,b∩c=M?a⊥α);③平行线垂直平面的传递性质(a∥b,b⊥α?a⊥α);
④面面垂直的性质(α⊥β,α∩β=l,a?β,a⊥l?a⊥α);
⑤面面平行的性质(a⊥α,α∥β?a⊥β);
⑥面面垂直的性质(α∩β=l,α⊥γ,β⊥γ?l⊥γ).
(3)面面垂直的判定方法:
①根据定义(作两平面构成二面角的平面角,计算其为90°);
②面面垂直的判定定理(a⊥β,a?α?α⊥β).题型四 空间角问题
[典例4] (2017·天津卷)如图,在四棱锥P-ABCD中,AD⊥平面PDC,AD∥BC,
PD⊥PB,AD=1,BC=3,CD=4,PD=2.(1)求异面直线AP与BC所成角的余弦值;(2)求证:PD⊥平面PBC;(2)证明:由(1)知AD⊥PD.
又因为BC∥AD,所以PD⊥BC.
又PD⊥PB,PB∩BC=B,所以PD⊥平面PBC.(3)求直线AB与平面PBC所成角的正弦值.规律方法求角度问题时,无论哪种情况最终都归结到两条相交直线所成的角的问题上,求角度的解题步骤是:(1)找出这个角;(2)证该角符合题意;(3)构造出含这个角的三角形,解这个三角形,求出角.空间角包括以下三类:
①两条异面直线所成的角,找两条异面直线所成的角,关键是选取合适的点引两条异面直线的平行线,这两条相交直线所成的锐角或直角即为两条异面直线所成的角.
②求直线与平面所成的角关键是确定斜线在平面内的射影.
③求二面角关键是作出二面角的平面角,而作二面角的平面角时,首先要确定二面角的棱,然后结合题设构造二面角的平面角.题型五 空间几何体中的体积计算
[典例5] (2018·合肥期末)如图所示,在直角梯形BCEF中,∠CBF=∠BCE=
90°,A,D分别是BF,CE上的点,AD∥BC,且DE=2AF=2AD(如图1).将四边形ADEF沿AD折起,使点E到达点G的位置,连接BG,BF,CG(如图2),且AB⊥GD.(1)证明:AC∥平面BFG;(2)当AB=DG=2,求三棱锥A-BCG的体积.规律方法(1)求空间几何体的体积的关键是确定几何体的高,若几何体的高容易求出,可直接代入体积公式计算,否则可用下列方法进行转化:
①等体积转化法:对于三棱锥因为任何一个面都可作为底面,所以在求三棱锥的体积时,可将其转化为底面积和高都易求的形式求解.
②补体法:将几何体补成易求体积的几何体,再根据它们的体积关系求解.
③分割法:将几何体分割为易求体积的几部分,分别求解再求和.
(2)有关平面图形翻折成空间图形的问题,应注意翻折前后各元素(直线、线段、角)的相对位置(平行、垂直)和数量的变化,搞清楚哪些发生了变化、哪些不变.题型六 易错辨析
[典例6] 如图,已知E,F分别是正方体ABCD-A1B1C1D1的棱AA1,CC1上的点,且AE=C1F.求证:四边形EBFD1是平行四边形.错解:因为平面A1ADD1∥平面B1BCC1,D1E=平面A1ADD1∩平面BFD1E,BF=平面B1BCC1∩平面BFD1E,所以D1E∥FB.同理可得D1F∥EB.
所以四边形EBFD1是平行四边形.
纠错:错解中盲目地认为E,B,F,D1四点共面,由已知条件并不能说明这四点共面,同时条件AE=C1F也没有用到.真题赏析·素养升级1.(2017·全国Ⅲ卷,文10)在正方体ABCD-A1B1C1D1中,E为棱CD的中点,则( )
(A)A1E⊥DC1 (B)A1E⊥BD
(C)A1E⊥BC1 (D)A1E⊥AC解析:如图,由题意可知
A1E?平面A1B1CD,
可以证明BC1⊥平面A1B1CD,
所以A1E⊥BC1,
故选C.C2.(2017·全国Ⅱ卷,理10)已知直三棱柱ABC-A1B1C1中,∠ABC=120°,AB=2,
BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为( )C解析:①可能有m⊥β,即α∥β,得①错,②③④正确.
答案:②③④3.(2016·全国Ⅱ卷,理14)α,β是两个平面,m,n是两条直线,有下列四个命题:
①如果m⊥n,m⊥α,n∥β,那么α⊥β.
②如果m⊥α,n∥α,那么m⊥n.
③如果α∥β,m?α,那么m∥β.
④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.
其中正确的命题有 .(填写所有正确命题的编号)?证明:(1)在平行六面体ABCD-A1B1C1D1中,
AB∥A1B1.
因为AB?平面A1B1C,A1B1?平面A1B1C,
所以AB∥平面A1B1C.4.(2018·江苏卷,15)在平行六面体ABCD-A1B1C1D1中,AA1=AB,AB1⊥B1C1.
求证:(1)AB∥平面A1B1C;证明:(2)在平行六面体ABCD-A1B1C1D1中,四边形ABB1A1为平行四边形.
又因为AA1=AB,所以四边形ABB1A1为菱形,
因此AB1⊥A1B.
又因为AB1⊥B1C1,BC∥B1C1,
所以AB1⊥BC.
又因为A1B∩BC=B,
A1B?平面A1BC,BC?平面A1BC,
所以AB1⊥平面A1BC.
因为AB1?平面ABB1A1,
所以平面ABB1A1⊥平面A1BC.(2)平面ABB1A1⊥平面A1BC.(1)证明:由已知可得,∠BAC=90°,
即BA⊥AC.
又BA⊥AD,AC∩AD=A.
所以AB⊥平面ACD.
又AB?平面ABC,
所以平面ACD⊥平面ABC.5.(2018·全国Ⅰ卷,文18)如图,在平行四边形ABCM中,AB=AC=3,∠ACM=
90°.以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.
(1)证明:平面ACD⊥平面ABC;(1)证明:由已知∠BAP=∠CDP=90°,得AB⊥AP,CD⊥PD.
由于AB∥CD,故AB⊥PD,又AP∩PD=P,
从而AB⊥平面PAD.
又AB?平面PAB,
所以平面PAB⊥平面PAD.6.(2017·全国Ⅰ卷,文18)如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=
∠CDP=90°.
(1)证明:平面PAB⊥平面PAD;
