人教A版高中数学必修二 课件 3.2.1 直线的点斜式方程 :30张PPT
文档属性
| 名称 | 人教A版高中数学必修二 课件 3.2.1 直线的点斜式方程 :30张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 00:00:00 | ||
图片预览











文档简介
课件30张PPT。3.2 直线的方程
3.2.1 直线的点斜式方程目标导航1.直线的点斜式方程
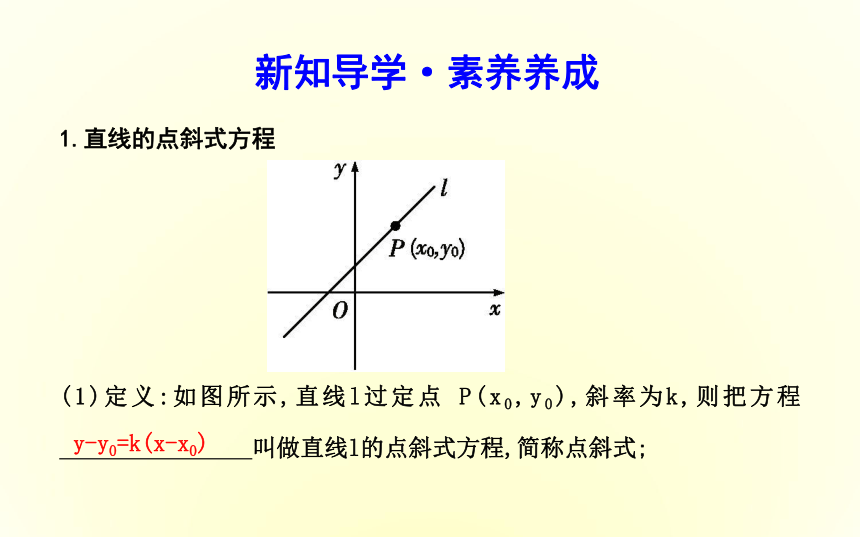
(1)定义:如图所示,直线l过定点 P(x0,y0),斜率为k,则把方程
叫做直线l的点斜式方程,简称点斜式;新知导学·素养养成y-y0=k(x-x0)(2)如图所示,过定点P(x0,y0),倾斜角是90°的直线没有点斜式,其方程为x-x0=0,或 .x=x0思考:直线的点斜式方程能否表示坐标平面内的所有直线?
答案:不能.当直线的斜率不存在时不能用点斜式表示.2.直线的斜截式方程
(1)定义:如图所示,直线l的斜率为k,且与y轴的交点为(0,b),则方程
叫做直线l的斜截式方程,简称斜截式;(2)一条直线与y轴的交点(0,b)的纵坐标b叫做直线在y轴上的 .倾斜角是 的直线没有斜截式方程.y=kx+b截距直角名师点津(1)经过点P0(x0,y0)的直线有无数条,可以分为两类:
①斜率存在的直线,方程为y-y0=k(x-x0);
②斜率不存在的直线,方程为x-x0=0,或x=x0.
(2)直线的斜截式方程
①斜截式方程应用的前提是直线的斜率存在.
②纵截距不是距离,它是直线与y轴交点的纵坐标,所以可取一切实数,即可为正数、负数或零.课堂探究·素养提升题型一 直线的点斜式方程
[例1] 写出下列直线的点斜式方程.
(1)经过点(2,5),倾斜角为45°;
(2)直线y=x+1绕着其上一点P(3,4)逆时针旋转90°后得直线l,求直线l的点斜式方程;解:(1)因为倾斜角为45°,所以斜率k=tan 45°=1,
所以直线的方程为y-5=x-2.
(2)直线y=x+1的斜率k=1,所以倾斜角为45°.
由题意知,直线l的倾斜角为135°,所以直线l的斜率k′=tan 135°=-1.
又点P(3,4)在直线l上,由点斜式方程知,直线l的方程为y-4=-(x-3).(3)经过点C(-1,-1),且与x轴平行;
(4)经过点D(1,1),且与x轴垂直.解:(3)由题意知,直线的斜率k=tan 0°=0,
所以直线的点斜式方程为y-(-1)=0,即y+1=0.
(4)由题意可知直线的斜率不存在,
所以直线的方程为x=1,该直线没有点斜式方程.误区警示利用点斜式求直线方程的方法
(1)用点斜式求直线的方程,首先要确定直线的斜率和其上一个点的坐标.注意在斜率存在的条件下,才能用点斜式表示直线的方程;当直线的斜率不存在时,直线方程为x=x0;
(2)已知两点坐标求直线的方程,可以先求斜率,再用点斜式求直线的方程.(2)设所求直线方程为3x+4y+m=0,代入(2,3)点,6+12+m=0,
解得m=-18.所以直线方程为3x+4y-18=0.(3)设所求直线方程为4x-3y+n=0,代入(2,3)点,8-9+n=0,
解得n=1.所以直线方程为4x-3y+1=0.2.求满足下列条件的直线的点斜式方程.
(1)过点P(-4,3),斜率k=-3;
(2)过点P(3,-4),且与x轴平行;
(3)过P(-2,3),Q(5,-4)两点.解:(1)因为直线过点P(-4,3),斜率k=-3,
由直线方程的点斜式得直线方程为y-3=-3(x+4),
(2)与x轴平行的直线,其斜率k=0,由直线方程的点斜式可得直线方程为y-(-4)=0×(x-3),即y+4=0.解:(1)由直线方程的斜截式可知,所求直线方程为y=2x+5.题型二 直线的斜截式方程
[例2] 根据条件写出下列直线的斜截式方程:
(1)斜率为2,在y轴上的截距是5;
(2)倾斜角为150°,在y轴上的截距是-2;(3)倾斜角为60°,与y轴的交点到坐标原点的距离为3.方法技巧(1)斜截式方程的应用前提是直线的斜率存在.当b=0时,y=kx表示过原点的直线;当k=0时,y=b表示与x轴平行(或重合)的直线.
(2)截距不同于日常生活中的距离,截距是一个点的横(纵)坐标,是一个实数,可以是正数,也可以是负数或零,而距离是一个非负数.即时训练2-1:已知直线l1的方程为y=-2x+3,l2的方程为y=4x-2,直线l与l1平行且与l2在y轴上的截距相等,求直线l的方程.解:由斜截式方程知直线l1的斜率k1=-2,
又因为l∥l1,
所以l的斜率k=k1=-2.
由题意知l2在y轴上的截距为-2,
所以l在y轴上的截距b=-2,
由斜截式可得直线l的方程为y=-2x-2.[备用例2]
1.直线l经过点(-2,2),且与直线y=x+6在y轴上有相等的截距,则直线l的方程为 .?解析:设直线l的方程为y=kx+6,将点(-2,2)代入,得2=-2k+6,解得k=2,所以直线l的方程为y=2x+6.
答案:y=2x+6题型三 平行垂直的应用
[例3] 当a为何值时,
(1)两直线y=ax-2与y=(a+2)x+1互相垂直?解:(1)设两直线的斜率分别为k1,k2,
则k1=a,k2=a+2.
因为两直线互相垂直,
所以k1k2=a(a+2)=-1,解得a=-1.
故当a=-1时,两条直线互相垂直.(2)两直线y=-x+4a与y=(a2-2)x+4互相平行?方法技巧对于不能用斜截式方程表示的直线,判断它们的位置关系时,需注意:
(1)若两条直线的斜率均不存在,则平行或重合.
(2)若一条直线的斜率不存在,另一条直线的斜率为0,则垂直.
(3)若一条直线的斜率不存在,另一条直线的斜率存在但不为0,则两条直线既不平行也不垂直.即时训练3-1:(1)当a为何值时,直线l1:y=-x+2a与直线l2:y=(a2-2)x+2平行?
(2)当a为何值时,直线l1:y=(2a-1)x+3与直线l2:y=4x-3垂直?2.△ABC中,A(1,-1),B(4,a),C(3,3).若△ABC是以B为直角的直角三角形.
(1)求a;(2)求直线AB的方程.课堂达标解析:因为方程可变形为y+2=-(x+1),
所以直线过点(-1,-2),斜率为-1.故选C.1.已知直线的方程是y+2=-x-1,则( )
(A)直线经过点(-1,2),斜率为-1
(B)直线经过点(2,-1),斜率为-1
(C)直线经过点(-1,-2),斜率为-1
(D)直线经过点(-2,-1),斜率为1C2.直线y=kx+b通过第一、三、四象限,则有( )
(A)k>0,b>0 (B)k>0,b<0
(C)k<0,b>0 (D)k<0,b<0B解析:因为直线经过一、三、四象限,
由图知,k>0,b<0.故选B.3.与直线y=2x+1垂直,且在y轴上的截距为4的直线的斜截式方程是( )D5.已知直线l的倾斜角是直线y=x+1的倾斜角的2倍,且过定点P(3,3),则直线l的方程为 .?解析:直线y=x+1的斜率为1,所以倾斜角为45°,又所求直线的倾斜角是已知直线倾斜角的2倍,所以所求直线的倾斜角为90°,其斜率不存在.又直线过定点P(3,3),所以直线l的方程为x=3.
答案:x=3
3.2.1 直线的点斜式方程目标导航1.直线的点斜式方程
(1)定义:如图所示,直线l过定点 P(x0,y0),斜率为k,则把方程
叫做直线l的点斜式方程,简称点斜式;新知导学·素养养成y-y0=k(x-x0)(2)如图所示,过定点P(x0,y0),倾斜角是90°的直线没有点斜式,其方程为x-x0=0,或 .x=x0思考:直线的点斜式方程能否表示坐标平面内的所有直线?
答案:不能.当直线的斜率不存在时不能用点斜式表示.2.直线的斜截式方程
(1)定义:如图所示,直线l的斜率为k,且与y轴的交点为(0,b),则方程
叫做直线l的斜截式方程,简称斜截式;(2)一条直线与y轴的交点(0,b)的纵坐标b叫做直线在y轴上的 .倾斜角是 的直线没有斜截式方程.y=kx+b截距直角名师点津(1)经过点P0(x0,y0)的直线有无数条,可以分为两类:
①斜率存在的直线,方程为y-y0=k(x-x0);
②斜率不存在的直线,方程为x-x0=0,或x=x0.
(2)直线的斜截式方程
①斜截式方程应用的前提是直线的斜率存在.
②纵截距不是距离,它是直线与y轴交点的纵坐标,所以可取一切实数,即可为正数、负数或零.课堂探究·素养提升题型一 直线的点斜式方程
[例1] 写出下列直线的点斜式方程.
(1)经过点(2,5),倾斜角为45°;
(2)直线y=x+1绕着其上一点P(3,4)逆时针旋转90°后得直线l,求直线l的点斜式方程;解:(1)因为倾斜角为45°,所以斜率k=tan 45°=1,
所以直线的方程为y-5=x-2.
(2)直线y=x+1的斜率k=1,所以倾斜角为45°.
由题意知,直线l的倾斜角为135°,所以直线l的斜率k′=tan 135°=-1.
又点P(3,4)在直线l上,由点斜式方程知,直线l的方程为y-4=-(x-3).(3)经过点C(-1,-1),且与x轴平行;
(4)经过点D(1,1),且与x轴垂直.解:(3)由题意知,直线的斜率k=tan 0°=0,
所以直线的点斜式方程为y-(-1)=0,即y+1=0.
(4)由题意可知直线的斜率不存在,
所以直线的方程为x=1,该直线没有点斜式方程.误区警示利用点斜式求直线方程的方法
(1)用点斜式求直线的方程,首先要确定直线的斜率和其上一个点的坐标.注意在斜率存在的条件下,才能用点斜式表示直线的方程;当直线的斜率不存在时,直线方程为x=x0;
(2)已知两点坐标求直线的方程,可以先求斜率,再用点斜式求直线的方程.(2)设所求直线方程为3x+4y+m=0,代入(2,3)点,6+12+m=0,
解得m=-18.所以直线方程为3x+4y-18=0.(3)设所求直线方程为4x-3y+n=0,代入(2,3)点,8-9+n=0,
解得n=1.所以直线方程为4x-3y+1=0.2.求满足下列条件的直线的点斜式方程.
(1)过点P(-4,3),斜率k=-3;
(2)过点P(3,-4),且与x轴平行;
(3)过P(-2,3),Q(5,-4)两点.解:(1)因为直线过点P(-4,3),斜率k=-3,
由直线方程的点斜式得直线方程为y-3=-3(x+4),
(2)与x轴平行的直线,其斜率k=0,由直线方程的点斜式可得直线方程为y-(-4)=0×(x-3),即y+4=0.解:(1)由直线方程的斜截式可知,所求直线方程为y=2x+5.题型二 直线的斜截式方程
[例2] 根据条件写出下列直线的斜截式方程:
(1)斜率为2,在y轴上的截距是5;
(2)倾斜角为150°,在y轴上的截距是-2;(3)倾斜角为60°,与y轴的交点到坐标原点的距离为3.方法技巧(1)斜截式方程的应用前提是直线的斜率存在.当b=0时,y=kx表示过原点的直线;当k=0时,y=b表示与x轴平行(或重合)的直线.
(2)截距不同于日常生活中的距离,截距是一个点的横(纵)坐标,是一个实数,可以是正数,也可以是负数或零,而距离是一个非负数.即时训练2-1:已知直线l1的方程为y=-2x+3,l2的方程为y=4x-2,直线l与l1平行且与l2在y轴上的截距相等,求直线l的方程.解:由斜截式方程知直线l1的斜率k1=-2,
又因为l∥l1,
所以l的斜率k=k1=-2.
由题意知l2在y轴上的截距为-2,
所以l在y轴上的截距b=-2,
由斜截式可得直线l的方程为y=-2x-2.[备用例2]
1.直线l经过点(-2,2),且与直线y=x+6在y轴上有相等的截距,则直线l的方程为 .?解析:设直线l的方程为y=kx+6,将点(-2,2)代入,得2=-2k+6,解得k=2,所以直线l的方程为y=2x+6.
答案:y=2x+6题型三 平行垂直的应用
[例3] 当a为何值时,
(1)两直线y=ax-2与y=(a+2)x+1互相垂直?解:(1)设两直线的斜率分别为k1,k2,
则k1=a,k2=a+2.
因为两直线互相垂直,
所以k1k2=a(a+2)=-1,解得a=-1.
故当a=-1时,两条直线互相垂直.(2)两直线y=-x+4a与y=(a2-2)x+4互相平行?方法技巧对于不能用斜截式方程表示的直线,判断它们的位置关系时,需注意:
(1)若两条直线的斜率均不存在,则平行或重合.
(2)若一条直线的斜率不存在,另一条直线的斜率为0,则垂直.
(3)若一条直线的斜率不存在,另一条直线的斜率存在但不为0,则两条直线既不平行也不垂直.即时训练3-1:(1)当a为何值时,直线l1:y=-x+2a与直线l2:y=(a2-2)x+2平行?
(2)当a为何值时,直线l1:y=(2a-1)x+3与直线l2:y=4x-3垂直?2.△ABC中,A(1,-1),B(4,a),C(3,3).若△ABC是以B为直角的直角三角形.
(1)求a;(2)求直线AB的方程.课堂达标解析:因为方程可变形为y+2=-(x+1),
所以直线过点(-1,-2),斜率为-1.故选C.1.已知直线的方程是y+2=-x-1,则( )
(A)直线经过点(-1,2),斜率为-1
(B)直线经过点(2,-1),斜率为-1
(C)直线经过点(-1,-2),斜率为-1
(D)直线经过点(-2,-1),斜率为1C2.直线y=kx+b通过第一、三、四象限,则有( )
(A)k>0,b>0 (B)k>0,b<0
(C)k<0,b>0 (D)k<0,b<0B解析:因为直线经过一、三、四象限,
由图知,k>0,b<0.故选B.3.与直线y=2x+1垂直,且在y轴上的截距为4的直线的斜截式方程是( )D5.已知直线l的倾斜角是直线y=x+1的倾斜角的2倍,且过定点P(3,3),则直线l的方程为 .?解析:直线y=x+1的斜率为1,所以倾斜角为45°,又所求直线的倾斜角是已知直线倾斜角的2倍,所以所求直线的倾斜角为90°,其斜率不存在.又直线过定点P(3,3),所以直线l的方程为x=3.
答案:x=3
