北师大版2019-2020九年级数学尖子生辅导训练试题(第十二周)解析版
文档属性
| 名称 | 北师大版2019-2020九年级数学尖子生辅导训练试题(第十二周)解析版 |

|
|
| 格式 | zip | ||
| 文件大小 | 380.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 00:00:00 | ||
图片预览


文档简介
2019-2020北师大版九年级数学相似三角形综合题尖子生辅导训练试题
(第十二周)
1.如图,直线 AB与坐标轴交与点 , 动点P沿路线 运动.
(1)求直线AB的表达式;
(2)当点P在OB上,使得AP平分 时,求此时点P的坐标;
2.在平面直角坐标系中,A(5,0),B(0,5).
(1)如图 1,P 是 AB 上一点且 ,求 P 点坐标;
(2)如图 2,D 为 OA 上一点,AC∥OB 且∠CBO=∠DCB,求∠CBD 的度数;
(3)如图 3,E 为 OA 上一点,OF⊥BE 于 F,若∠BEO=45°+∠EOF,求 的值
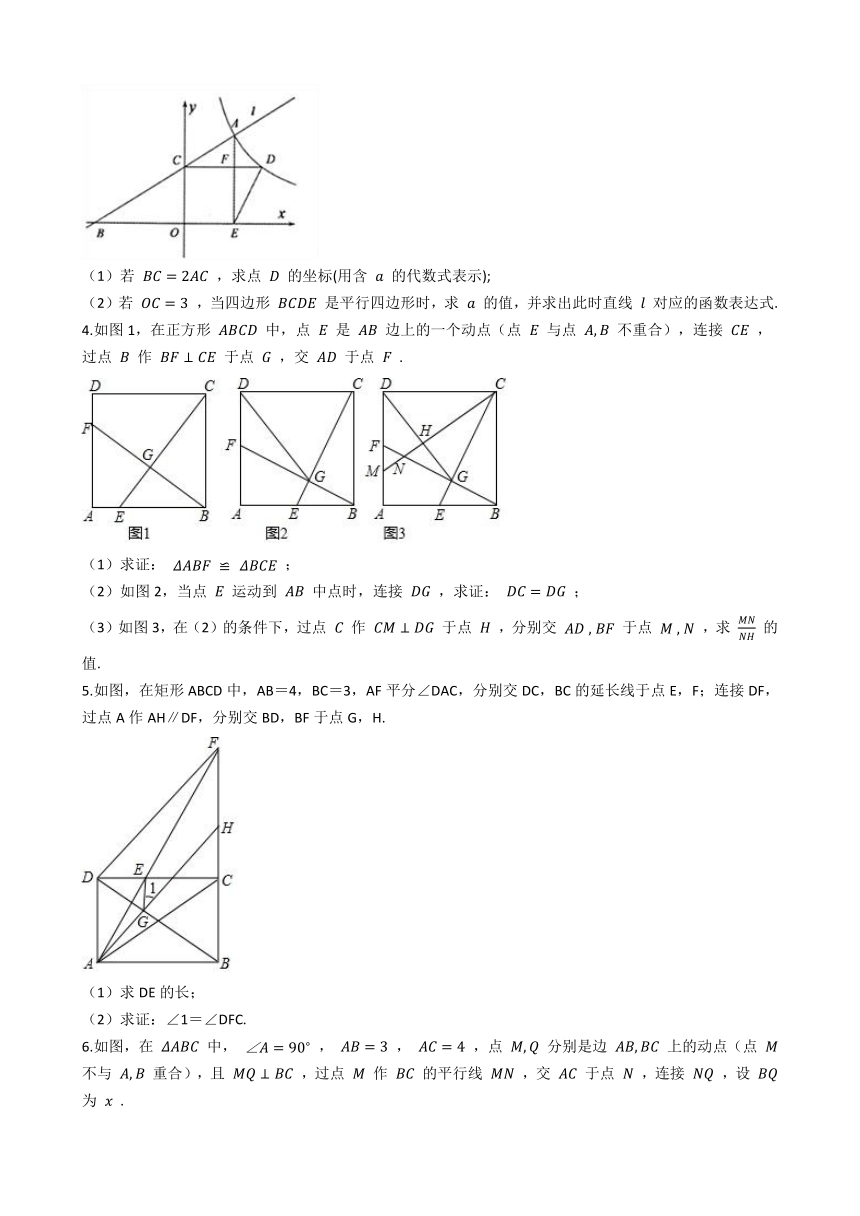
3.如图,已知点 是反比例函数 的图像上的一个动点,经过点 的直线 交 轴负半轴于点 ,交 轴正半轴于点 .过点 作 轴的垂线,交反比例函数的图像于点 .过点 作 轴于点 ,交 于点 ,连接 .设点 的横坐标是 .
(1)若 ,求点 的坐标(用含 的代数式表示);
(2)若 ,当四边形 是平行四边形时,求 的值,并求出此时直线 对应的函数表达式.
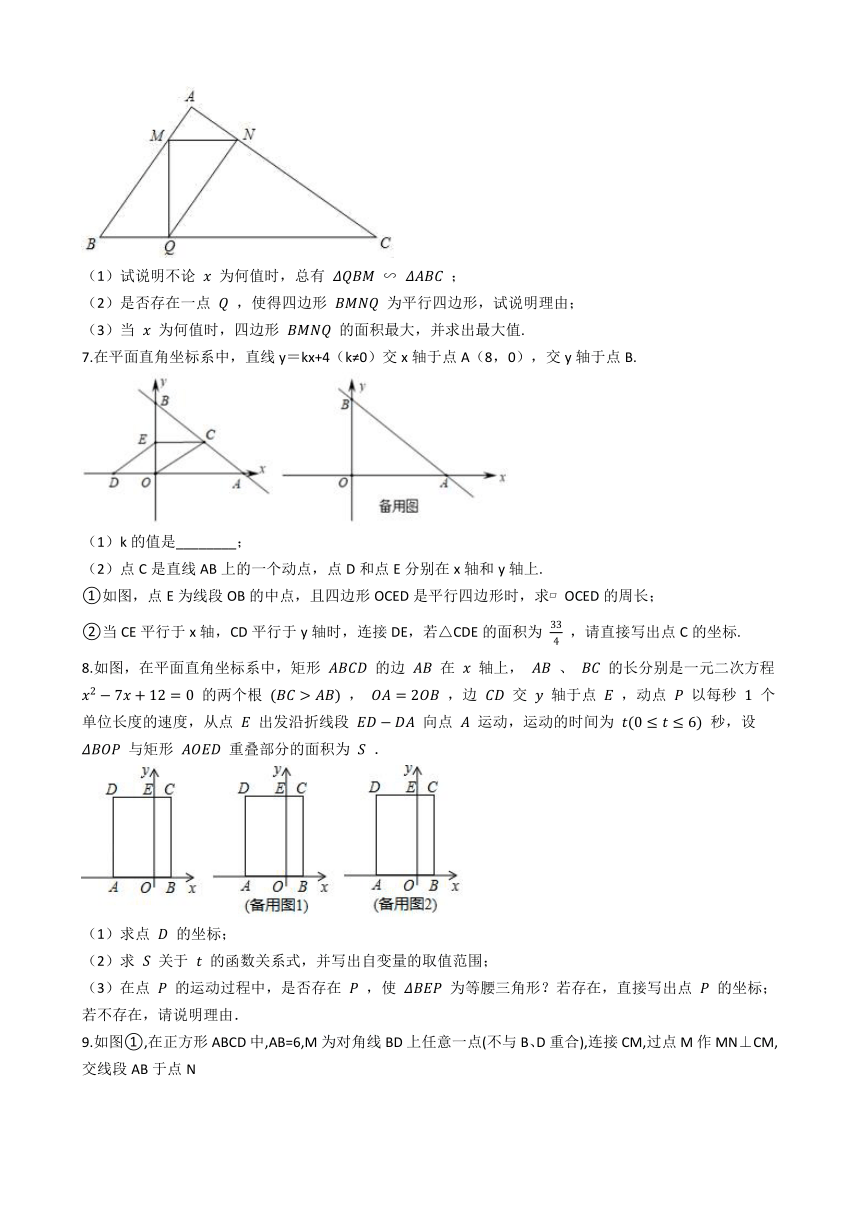
4.如图1,在正方形 中,点 是 边上的一个动点(点 与点 不重合),连接 ,过点 作 于点 ,交 于点 .
(1)求证: ;
(2)如图2,当点 运动到 中点时,连接 ,求证: ;
(3)如图3,在(2)的条件下,过点 作 于点 ,分别交 于点 ,求 的值.
5.如图,在矩形ABCD中,AB=4,BC=3,AF平分∠DAC,分别交DC,BC的延长线于点E,F;连接DF,过点A作AH∥DF,分别交BD,BF于点G,H.
(1)求DE的长;
(2)求证:∠1=∠DFC.
6.如图,在 中, , , ,点 分别是边 上的动点(点 不与 重合),且 ,过点 作 的平行线 ,交 于点 ,连接 ,设 为 .
(1)试说明不论 为何值时,总有 ∽ ;
(2)是否存在一点 ,使得四边形 为平行四边形,试说明理由;
(3)当 为何值时,四边形 的面积最大,并求出最大值.
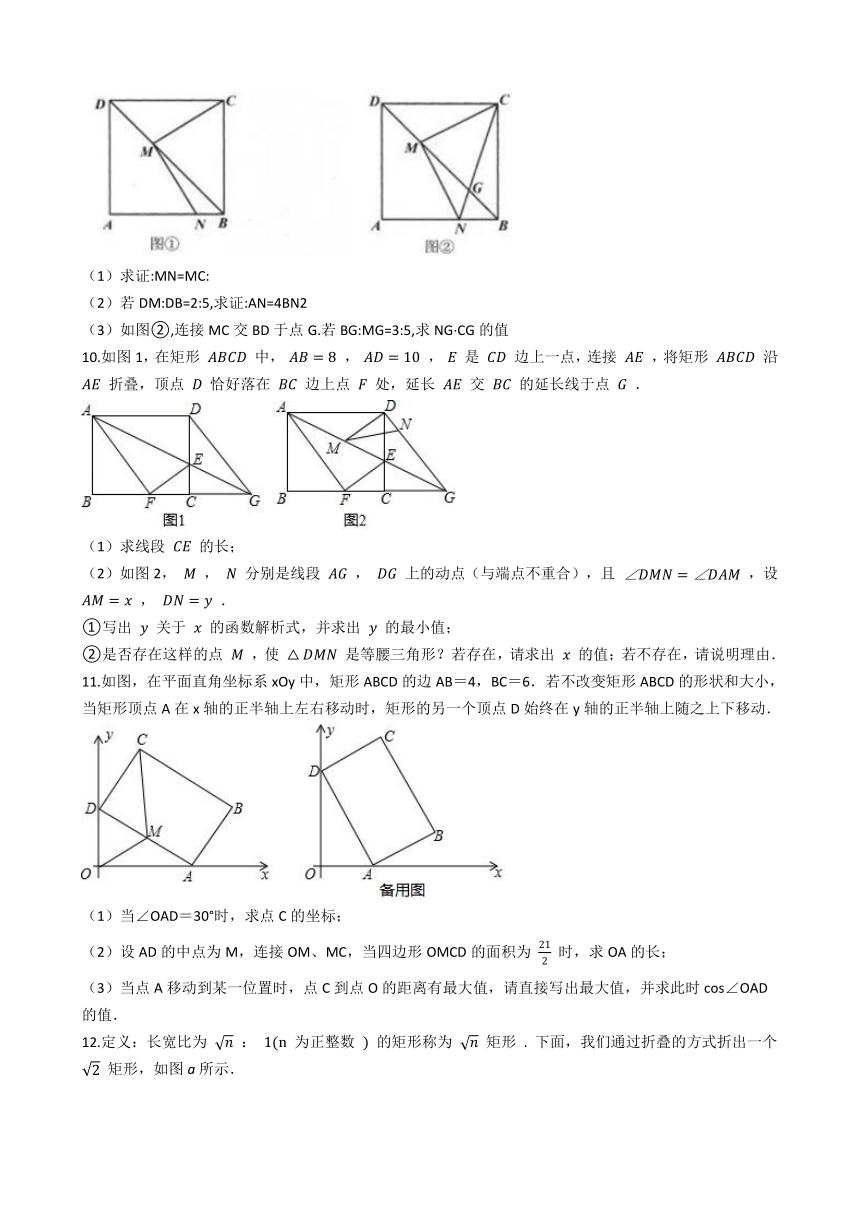
7.在平面直角坐标系中,直线y=kx+4(k≠0)交x轴于点A(8,0),交y轴于点B.
(1)k的值是________;
(2)点C是直线AB上的一个动点,点D和点E分别在x轴和y轴上.
①如图,点E为线段OB的中点,且四边形OCED是平行四边形时,求?OCED的周长;
②当CE平行于x轴,CD平行于y轴时,连接DE,若△CDE的面积为 ,请直接写出点C的坐标.
8.如图,在平面直角坐标系中,矩形 的边 在 轴上, 、 的长分别是一元二次方程 的两个根 , ,边 交 轴于点 ,动点 以每秒 个单位长度的速度,从点 出发沿折线段 向点 运动,运动的时间为 秒,设 与矩形 重叠部分的面积为 .
(1)求点 的坐标;
(2)求 关于 的函数关系式,并写出自变量的取值范围;
(3)在点 的运动过程中,是否存在 ,使 为等腰三角形?若存在,直接写出点 的坐标;若不存在,请说明理由.
9.如图①,在正方形ABCD中,AB=6,M为对角线BD上任意一点(不与B、D重合),连接CM,过点M作MN⊥CM,交线段AB于点N
(1)求证:MN=MC:
(2)若DM:DB=2:5,求证:AN=4BN2
(3)如图②,连接MC交BD于点G.若BG:MG=3:5,求NG·CG的值
10.如图1,在矩形 中, , , 是 边上一点,连接 ,将矩形 沿 折叠,顶点 恰好落在 边上点 处,延长 交 的延长线于点 .
(1)求线段 的长;
(2)如图2, , 分别是线段 , 上的动点(与端点不重合),且 ,设 , .
①写出 关于 的函数解析式,并求出 的最小值;
②是否存在这样的点 ,使 是等腰三角形?若存在,请求出 的值;若不存在,请说明理由.
11.如图,在平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=6.若不改变矩形ABCD的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在y轴的正半轴上随之上下移动.
(1)当∠OAD=30°时,求点C的坐标;
(2)设AD的中点为M,连接OM、MC,当四边形OMCD的面积为 时,求OA的长;
(3)当点A移动到某一位置时,点C到点O的距离有最大值,请直接写出最大值,并求此时cos∠OAD的值.
12.定义:长宽比为 : 为正整数 的矩形称为 矩形 下面,我们通过折叠的方式折出一个 矩形,如图a所示.
操作1:将正方形ABEF沿过点A的直线折叠,使折叠后的点B落在对角线AE上的点G处,折痕为AH .
操作2:过点G作CD∥AB,使点D、点C分别落在边AF , BE上.则四边形ABCD为 矩形.
(1)证明:四边形ABCD为 矩形;
(2)点M是边AB上一动点.
如图b , O是对角线AC的中点,若点N在边BC上, ,连接 求 的值;
连结AC,CM,当△AMC为等腰三角形时,将△CBM沿着CM翻折,点B的对称点为B’,连结AB’
求 的值.
13.如图,在平面直角坐标系中,过点A 的直线l分别与x轴、y轴交于点C,D.
(1)求直线l的函数表达式.
(2)P为x轴上一点,若△PCD为等腰三角形直接写出点P的坐标.
(3)将线段AB绕B点旋转90°,直接写出点A对应的点A的坐标.
14.如图,已知△ABC中,∠ACB=90°,AC=8,cosA= ,D是AB边的中点,E是AC边上一点,联结DE,过点D作DF⊥DE交BC边于点F,联结EF.
(1)如图1,当DE⊥AC时,求EF的长;
(2)如图2,当点E在AC边上移动时,∠DFE的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出∠DFE的正切值;
(3)如图3,联结CD交EF于点Q,当△CQF是等腰三角形时,请直接写出BF的长.
15.如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=10厘米,OC=6厘米,现有两动点P,Q分别从O,A同时出发,点P在线段OA上沿OA方向作匀速运动,点Q在线段AB上沿AB方向作匀速运动,已知点P的运动速度为1厘米/秒.
(1)设点Q的运动速度为0.5厘米/秒,运动时间为t秒,
①当△CPQ的面积最小时,求点Q的坐标;
②当△COP和△PAQ相似时,求点Q的坐标.
(2)设点Q的运动速度为a厘米/秒,问是否存在a的值,使得△OCP∽△PAQ∽CBQ?若存在,请求出a的值,并写出此时点Q的坐标;若不存在,请说明理由.
2019-2020北师大版九年级数学相似三角形综合题尖子生辅导训练试题
(第十二周)
1. (1)解:设直线AB的解析式为y=kx+b,
∵A(0,6),B(8,0),
∴ ,
∴ ,
∴直线AB的解析式为y= x+6
(2)解:方法1、如图1,
∵A(0,6),B(8,0),
∴OA=6,OB=8,AB=10,
过点B作BC∥OA交AP的延长线于C,
∴∠C=∠OAP,
∵AP平分∠OAB,
∴∠OAP=∠BAP,
∴∠C=∠BAP,
∴BC=AB=10,
∵BC∥OA,
∴△AOP∽△CBP,
∴ = ,
∴ ,
∴OP=3,
∴P(3,0);
方法2、如图3,过点P作PM⊥AB于M,
∵AP是∠OAB的角平分线,
∴OP=PM,
设OP=m,
∴PM=m,
∴BP=OB-OP=8-m
易知,△AOP≌△AMP,
∴AM=OA=6,
∴BM=AB-AM=4,
在Rt△BMP中,根据勾股定理得,m2+16=(8-m)2 ,
∴m=3,
∴P(3,0).
故答案为:(1)y= x+6;(2)P(3,0)
2. (1)解:作PG⊥x轴于G,PN⊥y轴于N,
∵
∴
∵A(5,0),B(0,5),
∴OA=5,OB=5,
∵PG⊥x轴,
∴PG∥OB,
∴△AGP∽△AOB,
∴ ,即 ,
解得,PG=2,
同理,PN=3,
∴P点坐标为(3,2)
(2)解:作BG⊥AC交AC的延长线于G,作BH⊥CD于H,
∴四边形BOAG为矩形,
∴BO=BG,
∵OA=OB,
∴矩形BOAG为正方形,
∵AC∥OB
∴∠CBO=∠BCG,
∵∠CBO=∠DCB,
∴∠BCG=∠DCB,
在△BCH和△BCG中,
?,
∴△BCH≌△BCG(AAS),
∴∠CBH=∠CBG,BG=BH,
∴BO=BH,
在Rt△BOD和Rt△BHD中,
?
∴Rt△BOD≌Rt△BHD(HL),
∴∠BOD=∠HOD,
∴∠CBD=∠DBH+∠CBH= ∠OBG=45°
(3)解:如图,
∵∠BEO=45°+∠EOF,∠BEO+∠EOF=90°,
∴∠BEO=67.5°,∠EOF=22.5°,
则∠OBE=22.5°,
作∠BOP=∠OBE=22.5°,
则PB=PO,∠OPF=45°,
设OF=a,则PF=OF=a,
由勾股定理得,OP= a,
∴PB= a,
∴BF= a+a,
∵∠BOP=∠OBE,∠OFB=∠EFO=90°,
∴△OFB∽△EFO,
∴EF= a-a,
∴
3. (1)解:∵点A的横坐标是a,∴点A的纵坐标为 ,∴AE= ,
∵AE⊥x轴,∴CO∥AE,∴△BOC∽△BEA,∴ = ,∴CO= ,
把y= 代入y= ,解得x= a,∴D点坐标为( a, )
(2)解:∵OC=3,∴D点纵坐标为3,把y=3代入y= 可得x=4,∴D(4,3),∴CD=4,
∵四边形BCDE是平行四边形,∴BE=CD=4,且CD∥BE,∴△ACF∽△ABE,
∴ ,即 = ,解得a=2,∴A(2,6),且C(0,3),
∴可设直线l的函数表达式为y=kx+3,把x=2,y=6代入,可得6=2k+3,解得k= ,
∴直线l的函数表达式为y= x+3.
4. (1)证明:∵ ,
∴ ,
∴ ,
∵四边形 是正方形,
∴ ,
∴ ,
∴ ,
∴
(2)证明:如图2,过点 作 于 ,
设 ,
∵点 是 的中点,
∴ ,
∴ ,
在 中,根据面积相等,得 ,
∴ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴
(3)解:如图3,过点 作 于 ,
,
∴ ,
在 中, ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
在 中, ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴
5. (1)解:∵矩形ABCD中,AD∥CF,
∴∠DAF=∠AFC,
∵AF平分∠DAC,
∴∠DAF=∠CAF,
∴∠FAC=∠AFC,
∴AC=CF,
∵AB=4,BC=3,
∴ = =5,
∴CF=5,
∵AD∥CF,
∴△ADE∽△FCE,
∴ ,
设DE=x,则 ,
解得x=
∴ ;
(2)证明:∵AD∥FH,AF∥DH,
∴四边形ADFH是平行四边形,
∴AD=FH=3,
∴CH=2,BH=5,
∵AD∥BH,
∴△ADG∽△HBG,
∴ ,
∴ ,
∴DG= ,
∵DE= ,
∴ = ,
∴EG∥BC,
∴∠1=∠AHC,
又∵DF∥AH,
∴∠AHC=∠DFC,
∠1=∠DFC.
6. (1)解:∵ ,
∴ ,
∴ ,又 ,
∴ ∽
(2)解:当 时,四边形 为平行四边形,
∵ , ,
∴四边形 为平行四边形
(3)解:∵ ,
∴ ,
∵ ∽ ,
∴ ,即 ,
解得, ,
∵ ,
∴ ,即 ,
解得, ,
则四边形 的面积 ,
∴当 时,四边形 的面积最大,最大值为 .
7. (1)
(2)①由(1)可知直线AB的解析式为y= x+4.
当x=0时,y= x+4=4,
∴点B的坐标为(0,4),
∴OB=4.
∵点E为OB的中点,
∴BE=OE= OB=2.
∵点A的坐标为(8,0),
∴OA=8.
∵四边形OCED是平行四边形,
∴CE∥DA,
∴ ,
∴BC=AC,
∴CE是△ABO的中位线,
∴CE= OA=4.
∵四边形OCED是平行四边形,
∴OD=CE=4,OC=DE.
在Rt△DOE中,∠DOE=90°,OD=4,OE=2,
∴DE= ,
∴C平行四边形OCED=2(OD+DE)=2(4+2 )=8+4 .
②设点C的坐标为(x, +4),则CE=|x|,CD=| x+4|,
∴S△CDE= CD?CE=|﹣ x2+2x|= ,
∴x2+8x+33=0或x2+8x﹣33=0.
方程x2+8x+33=0无解;
解方程x2+8x﹣33=0,得:x1=﹣3,x2=11,
∴点C的坐标为(﹣3, )或(11, ).
8. (1)解: ,
, ,
,
, ,
,
, ,
四边形 是矩形,
点 的坐标为
(2)解:设 交 轴于点 ,
如图1,当 时, ,
,
,
,即 ,
,
;
如图2,当 时, ,
,
,
,即 ,
,
;
综上所述,
(3)解:由题意知,当点 在 上时,显然不能构成等腰三角形;
当点 在 上运动时,设 ,
, ,
, , ,
①当 时, ,解得 ,
则 ;
②当 时, ,解得 ,
则 ;
③当 时, ,解得 ,
则 ;
综上, 或 或 .
9. (1)解:如图,过M分别作ME∥AB交BC于点E,MF∥BC交AB于点F,
则四边形BEMF是平行四边形
∵四边形ABCD是正方形,
∴∠ABC=90°,∠ABD=∠CBD=∠BME=45°
∴ME= BE
∴平行四边形MEBF是正方形.
∴ME=MF
∵CM⊥MN,
∴∠CMN=90°
∵∠FME=90°
∴.∠CME=∠FMN
∴△MFN≌△MEC,
∴MN=MC
(2)证明:由(1)得:FM∥AD,EM∥CD
.
AF=24.CE=24.
△MFN≌△MEC
∴FN=EC=2.4
N=4.8,BN=6-4.8=1.2
AN=4BN
(3)解:把△DMC绕点C逆时针旋转90°得到△BHC,连接GH
∵△DMC≌△BHC,∠BCD=90°,
∴MC=HC,DM=BH,∠CDM=∠CBH,∠DCM=∠BCH=45°
∴∠MBH=90°,∠MCH=90°
MC=MN,MC⊥MN
∴△MNC是等腰直角三角形
∠MNC=45°
∴∠NCH=45°
∴△MCG≌△HCG
∴MG=HG
∵BG:MG=3:5,
∴设BG=3a,则MG=GH=5a
在Rt△BGH中,BH= ?=4a,则MD=4a
∵正方形ABCD的边长为6,
.BD=6
∴DM+MG+BG=12a=6
∴a=
∴BG= ,MG=
∵∠MGC=∠NGB,∠MNG=∠GBC=45°
∴△MGC∽△MGB.
∴
∴CG·NG=BG·MG≈
10. (1)解:如图1中,
∵四边形 是矩形,
∴ , ,
∴ ,
由翻折可知: . ,设 ,则 .
在 中, ,
∴ ,
在 中,则有: ,
∴ ,
∴
(2)解:①如图2中,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
在 中, ,
在 中, ,
∵ ,
∴ ,
∵ , ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ .
当 时, 有最小值,最小值 .
②存在.有两种情形:如图3-1中,当 时,
∵ , ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ .
如图3-2中,当 时,作 于 .
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
由 ,可得 ,
∴ ,
∴ ,
∴ .
综上所述,满足条件的 的值为 或
11. (1)解:如图1,过点C作CE⊥y轴于点E,
∵矩形ABCD中,CD⊥AD,
∴∠CDE+∠ADO=90°,
又∵∠OAD+∠ADO=90°,
∴∠CDE=∠OAD=30°,
∴在Rt△CED中,CE= CD=2,DE= =2 ,
在Rt△OAD中,∠OAD=30°,
∴OD= AD=3,
∴点C的坐标为(2,3+2 )
(2)解:∵M为AD的中点,
∴DM=3,S△DCM=6,
又S四边形OMCD= ,
∴S△ODM= ,
∴S△OAD=9,
设OA=x、OD=y,则x2+y2=36, xy=9,
∴x2+y2=2xy,即x=y,
将x=y代入x2+y2=36得x2=18,
解得x=3 (负值舍去),
∴OA=3
(3)解:OC的最大值为8,
如图2,M为AD的中点,
∴OM=3,CM= =5,
∴OC≤OM+CM=8,
当O、M、C三点在同一直线时,OC有最大值8,
连接OC,则此时OC与AD的交点为M,过点O作ON⊥AD,垂足为N,
∵∠CDM=∠ONM=90°,∠CMD=∠OMN,
∴△CMD∽△OMN,
∴ ,即 ,
解得MN= ,ON= ,
∴AN=AM﹣MN= ,
在Rt△OAN中,OA= ,
∴cos∠OAD=
12. (1)证明:设正方形ABEF的边长为a,
∵AE是正方形ABEF的对角线,
∴∠DAG=45? ,
由折叠性质可知AG=AB=a,
∠FDC=∠ADC=90? ,
则四边形ABCD为矩形,
∴△ADG是等腰直角三角形.
∴AD=DG=a,
∴AB:AD=a:a=:1.
∴四边形ABCD为矩形;
(2)解:如图,作OP⊥AB,OQ⊥BC,垂足分别为P,Q.
∵四边形ABCD是矩形,∠B=90? , ∴四边形BQOP是矩形. ∴∠POQ=90? , OP//BC,OQ//AB. ∴OP:BC=AO:AC,OQ:AB=CO:CA. ∵O为AC中点, ∴OP=BC,OQ=AB. ∵∠MON=90? , ∴∠QON=∠POM. ∴Rt△QON∽Rt△POM. ∴ON:OM=OQ:OP=AB:BC=. ∴tan∠OMN=ON:OM=.
②解:设AM=x, 则BM=a-x, MC=AM=x, 在Rt△BMC中,由勾股定理得,MC2=BM2+BC2 ,
x2=(a-x)2+a2, 解得x=a , ∵∠PB‘C+∠QB’M=90°,∠PB‘C+∠PCB‘=90°,∴∠QB’M=∠PCB‘,
∴△PB’C≌△QB'M,得B'Q:PC=B'M:B'C,设 B‘Q=x, 则x:PC=(a-a):a, 解得PC=2x,
在△CB’P中,由勾股定理得PC2+PB'2=CB'2 , (2x)2+(a-x)2=a2, 解得x=a ,
∴S△AB'M=AM×B'Q=a×a=a2,
S△AB'C=S△ABC-2S△MBC-S△AB'M=a2-2×a×a-a2=a2,
∴.
13. (1)解:设直线l的函数表达式为y=kx+b(k≠0),
将A(1, ),B(4, )代入y=kx+b,
得: ,解得: ,
∴直线l的函数表达式为y=﹣ x+8
(2)解:当x=0时,y=﹣ x+8=8,
∴点D的坐标为(0,8);
当y=0时,﹣ x+8=0,
解得:x=6,
∴点C的坐标为(6,0),
∴CD=10.
分三种情况考虑(如图1所示):
①当DC=DP时,OC=OP1 ,
∴点P1的坐标为(﹣6,0);
②当CD=CP时,CP=10,
∴点P2的坐标为(﹣4,0),点P3的坐标为(16,0);
③当PC=PD时,设OP4=m,
∴(6+m)2=82+m2 ,
解得:m= ,
∴点P4的坐标为(﹣ ,0).
综上所述:点P的坐标为(﹣6,0),(﹣4,0),(16,0)或(﹣ ,0)
(3)解:过点B作直线l的垂线,交y轴于点E,如图2所示,
∵点B(4, ),点D(0,8),
∴BD= = ,
∵∠CDO=∠EDB,∠DOC=∠DBE=90°,
∴△DOC∽△DBE,
∴ ,即 ,
∴DE= ,
∴点E的坐标为(0,﹣ ).
利用待定系数法可求出直线BE的函数表达式为y= x﹣ ,
设点A′的坐标为(n, n﹣ ),
∵A′B=AB,
∴(4﹣n)2+[ ﹣( n﹣ )]2=(4﹣1)2+( ﹣ )2 ,
即n2﹣8n=0,
解得:n1=0,n2=8,
∴点A′的坐标为(0,﹣ )或(8, ).
14. (1)解:∵ ,
∴
∵
∴
∵ 是 边的中点
∴
∵
∴
∴
∴
∴
∵在 中,
∴
∵
∴
又∵
∴四边形 是矩形
∴
∵在 中,
∴
(2)解:不变
过点 作 , ,垂足分别为点 、
由(1)可得 ,
∵ ,
∴
又∵ ,
∴四边形 是矩形
∴
∵
∴ 即
又∵
∴
∴
∵
∴
(3)解:1°当 时,易证 ,即
又∵ ,D是AB的中点
∴
∴
2°当 时,易证
∵在 中,
∴设 ,则 ,
当 时,易证 ,
∴
∵
∴
∴
∴
∵
∴
∴ 解得
∴
∴
3°在BC边上截取BK=BD=5,由勾股定理得出
当 时,易证
∴设 ,则 ,
∴
∵
∴
∴
∴
∵
∴
∴ 解得
∴
∴
15. (1)解:①先设两点运动的时间是t时,△CPQ面积最小.
S△CPQ=S梯形QCOA﹣S△COP﹣S△APQ= (AQ+OC)×OA﹣ AP?AQ﹣ OC?OP
= (0.5t+6)×10﹣ ×0.5t×(10﹣t)﹣ ×6×t
= (t﹣6)2+21
∵a= >0,
∴当t=6时,S△CPQ有最小值,
那么AQ=0.5t=0.5×6=3,
∴Q点的坐标是(10,3).
②△COP和△PAQ相似,有△COP∽△PAQ和△COP∽△QAP两种情况:
(i)当△COP∽△PAQ时:
∴ = ,
∴ = ,
即t2﹣7t=0,
解得,t1=0(不合题意,舍去),t2=7.
∴t=7,
∴AQ=0.5t=0.5×7=3.5.
∴Q点的坐标是(10,3.5).
(ii)当△COP∽△QAP时:
= ,
∴ = ,
即t2+12t﹣120=0
解得:t1=﹣6+2 ,t2=﹣6﹣2 (不合题意,舍去)
∴AQ=0.5t=﹣3+ .
∴Q点的坐标是(10,﹣3+ );
(2)解:∵△COP∽△PAQ∽△CBQ,
∴ ,
即 ,
解得,t1=2,t2=18,
又∵0<t<10,
∴t=2.代入任何一个式子,可求a= .
∴AQ=at=
∴Q点的坐标是(10, ).
(第十二周)
1.如图,直线 AB与坐标轴交与点 , 动点P沿路线 运动.
(1)求直线AB的表达式;
(2)当点P在OB上,使得AP平分 时,求此时点P的坐标;
2.在平面直角坐标系中,A(5,0),B(0,5).
(1)如图 1,P 是 AB 上一点且 ,求 P 点坐标;
(2)如图 2,D 为 OA 上一点,AC∥OB 且∠CBO=∠DCB,求∠CBD 的度数;
(3)如图 3,E 为 OA 上一点,OF⊥BE 于 F,若∠BEO=45°+∠EOF,求 的值
3.如图,已知点 是反比例函数 的图像上的一个动点,经过点 的直线 交 轴负半轴于点 ,交 轴正半轴于点 .过点 作 轴的垂线,交反比例函数的图像于点 .过点 作 轴于点 ,交 于点 ,连接 .设点 的横坐标是 .
(1)若 ,求点 的坐标(用含 的代数式表示);
(2)若 ,当四边形 是平行四边形时,求 的值,并求出此时直线 对应的函数表达式.
4.如图1,在正方形 中,点 是 边上的一个动点(点 与点 不重合),连接 ,过点 作 于点 ,交 于点 .
(1)求证: ;
(2)如图2,当点 运动到 中点时,连接 ,求证: ;
(3)如图3,在(2)的条件下,过点 作 于点 ,分别交 于点 ,求 的值.
5.如图,在矩形ABCD中,AB=4,BC=3,AF平分∠DAC,分别交DC,BC的延长线于点E,F;连接DF,过点A作AH∥DF,分别交BD,BF于点G,H.
(1)求DE的长;
(2)求证:∠1=∠DFC.
6.如图,在 中, , , ,点 分别是边 上的动点(点 不与 重合),且 ,过点 作 的平行线 ,交 于点 ,连接 ,设 为 .
(1)试说明不论 为何值时,总有 ∽ ;
(2)是否存在一点 ,使得四边形 为平行四边形,试说明理由;
(3)当 为何值时,四边形 的面积最大,并求出最大值.
7.在平面直角坐标系中,直线y=kx+4(k≠0)交x轴于点A(8,0),交y轴于点B.
(1)k的值是________;
(2)点C是直线AB上的一个动点,点D和点E分别在x轴和y轴上.
①如图,点E为线段OB的中点,且四边形OCED是平行四边形时,求?OCED的周长;
②当CE平行于x轴,CD平行于y轴时,连接DE,若△CDE的面积为 ,请直接写出点C的坐标.
8.如图,在平面直角坐标系中,矩形 的边 在 轴上, 、 的长分别是一元二次方程 的两个根 , ,边 交 轴于点 ,动点 以每秒 个单位长度的速度,从点 出发沿折线段 向点 运动,运动的时间为 秒,设 与矩形 重叠部分的面积为 .
(1)求点 的坐标;
(2)求 关于 的函数关系式,并写出自变量的取值范围;
(3)在点 的运动过程中,是否存在 ,使 为等腰三角形?若存在,直接写出点 的坐标;若不存在,请说明理由.
9.如图①,在正方形ABCD中,AB=6,M为对角线BD上任意一点(不与B、D重合),连接CM,过点M作MN⊥CM,交线段AB于点N
(1)求证:MN=MC:
(2)若DM:DB=2:5,求证:AN=4BN2
(3)如图②,连接MC交BD于点G.若BG:MG=3:5,求NG·CG的值
10.如图1,在矩形 中, , , 是 边上一点,连接 ,将矩形 沿 折叠,顶点 恰好落在 边上点 处,延长 交 的延长线于点 .
(1)求线段 的长;
(2)如图2, , 分别是线段 , 上的动点(与端点不重合),且 ,设 , .
①写出 关于 的函数解析式,并求出 的最小值;
②是否存在这样的点 ,使 是等腰三角形?若存在,请求出 的值;若不存在,请说明理由.
11.如图,在平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=6.若不改变矩形ABCD的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在y轴的正半轴上随之上下移动.
(1)当∠OAD=30°时,求点C的坐标;
(2)设AD的中点为M,连接OM、MC,当四边形OMCD的面积为 时,求OA的长;
(3)当点A移动到某一位置时,点C到点O的距离有最大值,请直接写出最大值,并求此时cos∠OAD的值.
12.定义:长宽比为 : 为正整数 的矩形称为 矩形 下面,我们通过折叠的方式折出一个 矩形,如图a所示.
操作1:将正方形ABEF沿过点A的直线折叠,使折叠后的点B落在对角线AE上的点G处,折痕为AH .
操作2:过点G作CD∥AB,使点D、点C分别落在边AF , BE上.则四边形ABCD为 矩形.
(1)证明:四边形ABCD为 矩形;
(2)点M是边AB上一动点.
如图b , O是对角线AC的中点,若点N在边BC上, ,连接 求 的值;
连结AC,CM,当△AMC为等腰三角形时,将△CBM沿着CM翻折,点B的对称点为B’,连结AB’
求 的值.
13.如图,在平面直角坐标系中,过点A 的直线l分别与x轴、y轴交于点C,D.
(1)求直线l的函数表达式.
(2)P为x轴上一点,若△PCD为等腰三角形直接写出点P的坐标.
(3)将线段AB绕B点旋转90°,直接写出点A对应的点A的坐标.
14.如图,已知△ABC中,∠ACB=90°,AC=8,cosA= ,D是AB边的中点,E是AC边上一点,联结DE,过点D作DF⊥DE交BC边于点F,联结EF.
(1)如图1,当DE⊥AC时,求EF的长;
(2)如图2,当点E在AC边上移动时,∠DFE的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出∠DFE的正切值;
(3)如图3,联结CD交EF于点Q,当△CQF是等腰三角形时,请直接写出BF的长.
15.如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=10厘米,OC=6厘米,现有两动点P,Q分别从O,A同时出发,点P在线段OA上沿OA方向作匀速运动,点Q在线段AB上沿AB方向作匀速运动,已知点P的运动速度为1厘米/秒.
(1)设点Q的运动速度为0.5厘米/秒,运动时间为t秒,
①当△CPQ的面积最小时,求点Q的坐标;
②当△COP和△PAQ相似时,求点Q的坐标.
(2)设点Q的运动速度为a厘米/秒,问是否存在a的值,使得△OCP∽△PAQ∽CBQ?若存在,请求出a的值,并写出此时点Q的坐标;若不存在,请说明理由.
2019-2020北师大版九年级数学相似三角形综合题尖子生辅导训练试题
(第十二周)
1. (1)解:设直线AB的解析式为y=kx+b,
∵A(0,6),B(8,0),
∴ ,
∴ ,
∴直线AB的解析式为y= x+6
(2)解:方法1、如图1,
∵A(0,6),B(8,0),
∴OA=6,OB=8,AB=10,
过点B作BC∥OA交AP的延长线于C,
∴∠C=∠OAP,
∵AP平分∠OAB,
∴∠OAP=∠BAP,
∴∠C=∠BAP,
∴BC=AB=10,
∵BC∥OA,
∴△AOP∽△CBP,
∴ = ,
∴ ,
∴OP=3,
∴P(3,0);
方法2、如图3,过点P作PM⊥AB于M,
∵AP是∠OAB的角平分线,
∴OP=PM,
设OP=m,
∴PM=m,
∴BP=OB-OP=8-m
易知,△AOP≌△AMP,
∴AM=OA=6,
∴BM=AB-AM=4,
在Rt△BMP中,根据勾股定理得,m2+16=(8-m)2 ,
∴m=3,
∴P(3,0).
故答案为:(1)y= x+6;(2)P(3,0)
2. (1)解:作PG⊥x轴于G,PN⊥y轴于N,
∵
∴
∵A(5,0),B(0,5),
∴OA=5,OB=5,
∵PG⊥x轴,
∴PG∥OB,
∴△AGP∽△AOB,
∴ ,即 ,
解得,PG=2,
同理,PN=3,
∴P点坐标为(3,2)
(2)解:作BG⊥AC交AC的延长线于G,作BH⊥CD于H,
∴四边形BOAG为矩形,
∴BO=BG,
∵OA=OB,
∴矩形BOAG为正方形,
∵AC∥OB
∴∠CBO=∠BCG,
∵∠CBO=∠DCB,
∴∠BCG=∠DCB,
在△BCH和△BCG中,
?,
∴△BCH≌△BCG(AAS),
∴∠CBH=∠CBG,BG=BH,
∴BO=BH,
在Rt△BOD和Rt△BHD中,
?
∴Rt△BOD≌Rt△BHD(HL),
∴∠BOD=∠HOD,
∴∠CBD=∠DBH+∠CBH= ∠OBG=45°
(3)解:如图,
∵∠BEO=45°+∠EOF,∠BEO+∠EOF=90°,
∴∠BEO=67.5°,∠EOF=22.5°,
则∠OBE=22.5°,
作∠BOP=∠OBE=22.5°,
则PB=PO,∠OPF=45°,
设OF=a,则PF=OF=a,
由勾股定理得,OP= a,
∴PB= a,
∴BF= a+a,
∵∠BOP=∠OBE,∠OFB=∠EFO=90°,
∴△OFB∽△EFO,
∴EF= a-a,
∴
3. (1)解:∵点A的横坐标是a,∴点A的纵坐标为 ,∴AE= ,
∵AE⊥x轴,∴CO∥AE,∴△BOC∽△BEA,∴ = ,∴CO= ,
把y= 代入y= ,解得x= a,∴D点坐标为( a, )
(2)解:∵OC=3,∴D点纵坐标为3,把y=3代入y= 可得x=4,∴D(4,3),∴CD=4,
∵四边形BCDE是平行四边形,∴BE=CD=4,且CD∥BE,∴△ACF∽△ABE,
∴ ,即 = ,解得a=2,∴A(2,6),且C(0,3),
∴可设直线l的函数表达式为y=kx+3,把x=2,y=6代入,可得6=2k+3,解得k= ,
∴直线l的函数表达式为y= x+3.
4. (1)证明:∵ ,
∴ ,
∴ ,
∵四边形 是正方形,
∴ ,
∴ ,
∴ ,
∴
(2)证明:如图2,过点 作 于 ,
设 ,
∵点 是 的中点,
∴ ,
∴ ,
在 中,根据面积相等,得 ,
∴ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴
(3)解:如图3,过点 作 于 ,
,
∴ ,
在 中, ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
在 中, ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴
5. (1)解:∵矩形ABCD中,AD∥CF,
∴∠DAF=∠AFC,
∵AF平分∠DAC,
∴∠DAF=∠CAF,
∴∠FAC=∠AFC,
∴AC=CF,
∵AB=4,BC=3,
∴ = =5,
∴CF=5,
∵AD∥CF,
∴△ADE∽△FCE,
∴ ,
设DE=x,则 ,
解得x=
∴ ;
(2)证明:∵AD∥FH,AF∥DH,
∴四边形ADFH是平行四边形,
∴AD=FH=3,
∴CH=2,BH=5,
∵AD∥BH,
∴△ADG∽△HBG,
∴ ,
∴ ,
∴DG= ,
∵DE= ,
∴ = ,
∴EG∥BC,
∴∠1=∠AHC,
又∵DF∥AH,
∴∠AHC=∠DFC,
∠1=∠DFC.
6. (1)解:∵ ,
∴ ,
∴ ,又 ,
∴ ∽
(2)解:当 时,四边形 为平行四边形,
∵ , ,
∴四边形 为平行四边形
(3)解:∵ ,
∴ ,
∵ ∽ ,
∴ ,即 ,
解得, ,
∵ ,
∴ ,即 ,
解得, ,
则四边形 的面积 ,
∴当 时,四边形 的面积最大,最大值为 .
7. (1)
(2)①由(1)可知直线AB的解析式为y= x+4.
当x=0时,y= x+4=4,
∴点B的坐标为(0,4),
∴OB=4.
∵点E为OB的中点,
∴BE=OE= OB=2.
∵点A的坐标为(8,0),
∴OA=8.
∵四边形OCED是平行四边形,
∴CE∥DA,
∴ ,
∴BC=AC,
∴CE是△ABO的中位线,
∴CE= OA=4.
∵四边形OCED是平行四边形,
∴OD=CE=4,OC=DE.
在Rt△DOE中,∠DOE=90°,OD=4,OE=2,
∴DE= ,
∴C平行四边形OCED=2(OD+DE)=2(4+2 )=8+4 .
②设点C的坐标为(x, +4),则CE=|x|,CD=| x+4|,
∴S△CDE= CD?CE=|﹣ x2+2x|= ,
∴x2+8x+33=0或x2+8x﹣33=0.
方程x2+8x+33=0无解;
解方程x2+8x﹣33=0,得:x1=﹣3,x2=11,
∴点C的坐标为(﹣3, )或(11, ).
8. (1)解: ,
, ,
,
, ,
,
, ,
四边形 是矩形,
点 的坐标为
(2)解:设 交 轴于点 ,
如图1,当 时, ,
,
,
,即 ,
,
;
如图2,当 时, ,
,
,
,即 ,
,
;
综上所述,
(3)解:由题意知,当点 在 上时,显然不能构成等腰三角形;
当点 在 上运动时,设 ,
, ,
, , ,
①当 时, ,解得 ,
则 ;
②当 时, ,解得 ,
则 ;
③当 时, ,解得 ,
则 ;
综上, 或 或 .
9. (1)解:如图,过M分别作ME∥AB交BC于点E,MF∥BC交AB于点F,
则四边形BEMF是平行四边形
∵四边形ABCD是正方形,
∴∠ABC=90°,∠ABD=∠CBD=∠BME=45°
∴ME= BE
∴平行四边形MEBF是正方形.
∴ME=MF
∵CM⊥MN,
∴∠CMN=90°
∵∠FME=90°
∴.∠CME=∠FMN
∴△MFN≌△MEC,
∴MN=MC
(2)证明:由(1)得:FM∥AD,EM∥CD
.
AF=24.CE=24.
△MFN≌△MEC
∴FN=EC=2.4
N=4.8,BN=6-4.8=1.2
AN=4BN
(3)解:把△DMC绕点C逆时针旋转90°得到△BHC,连接GH
∵△DMC≌△BHC,∠BCD=90°,
∴MC=HC,DM=BH,∠CDM=∠CBH,∠DCM=∠BCH=45°
∴∠MBH=90°,∠MCH=90°
MC=MN,MC⊥MN
∴△MNC是等腰直角三角形
∠MNC=45°
∴∠NCH=45°
∴△MCG≌△HCG
∴MG=HG
∵BG:MG=3:5,
∴设BG=3a,则MG=GH=5a
在Rt△BGH中,BH= ?=4a,则MD=4a
∵正方形ABCD的边长为6,
.BD=6
∴DM+MG+BG=12a=6
∴a=
∴BG= ,MG=
∵∠MGC=∠NGB,∠MNG=∠GBC=45°
∴△MGC∽△MGB.
∴
∴CG·NG=BG·MG≈
10. (1)解:如图1中,
∵四边形 是矩形,
∴ , ,
∴ ,
由翻折可知: . ,设 ,则 .
在 中, ,
∴ ,
在 中,则有: ,
∴ ,
∴
(2)解:①如图2中,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
在 中, ,
在 中, ,
∵ ,
∴ ,
∵ , ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ .
当 时, 有最小值,最小值 .
②存在.有两种情形:如图3-1中,当 时,
∵ , ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ .
如图3-2中,当 时,作 于 .
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
由 ,可得 ,
∴ ,
∴ ,
∴ .
综上所述,满足条件的 的值为 或
11. (1)解:如图1,过点C作CE⊥y轴于点E,
∵矩形ABCD中,CD⊥AD,
∴∠CDE+∠ADO=90°,
又∵∠OAD+∠ADO=90°,
∴∠CDE=∠OAD=30°,
∴在Rt△CED中,CE= CD=2,DE= =2 ,
在Rt△OAD中,∠OAD=30°,
∴OD= AD=3,
∴点C的坐标为(2,3+2 )
(2)解:∵M为AD的中点,
∴DM=3,S△DCM=6,
又S四边形OMCD= ,
∴S△ODM= ,
∴S△OAD=9,
设OA=x、OD=y,则x2+y2=36, xy=9,
∴x2+y2=2xy,即x=y,
将x=y代入x2+y2=36得x2=18,
解得x=3 (负值舍去),
∴OA=3
(3)解:OC的最大值为8,
如图2,M为AD的中点,
∴OM=3,CM= =5,
∴OC≤OM+CM=8,
当O、M、C三点在同一直线时,OC有最大值8,
连接OC,则此时OC与AD的交点为M,过点O作ON⊥AD,垂足为N,
∵∠CDM=∠ONM=90°,∠CMD=∠OMN,
∴△CMD∽△OMN,
∴ ,即 ,
解得MN= ,ON= ,
∴AN=AM﹣MN= ,
在Rt△OAN中,OA= ,
∴cos∠OAD=
12. (1)证明:设正方形ABEF的边长为a,
∵AE是正方形ABEF的对角线,
∴∠DAG=45? ,
由折叠性质可知AG=AB=a,
∠FDC=∠ADC=90? ,
则四边形ABCD为矩形,
∴△ADG是等腰直角三角形.
∴AD=DG=a,
∴AB:AD=a:a=:1.
∴四边形ABCD为矩形;
(2)解:如图,作OP⊥AB,OQ⊥BC,垂足分别为P,Q.
∵四边形ABCD是矩形,∠B=90? , ∴四边形BQOP是矩形. ∴∠POQ=90? , OP//BC,OQ//AB. ∴OP:BC=AO:AC,OQ:AB=CO:CA. ∵O为AC中点, ∴OP=BC,OQ=AB. ∵∠MON=90? , ∴∠QON=∠POM. ∴Rt△QON∽Rt△POM. ∴ON:OM=OQ:OP=AB:BC=. ∴tan∠OMN=ON:OM=.
②解:设AM=x, 则BM=a-x, MC=AM=x, 在Rt△BMC中,由勾股定理得,MC2=BM2+BC2 ,
x2=(a-x)2+a2, 解得x=a , ∵∠PB‘C+∠QB’M=90°,∠PB‘C+∠PCB‘=90°,∴∠QB’M=∠PCB‘,
∴△PB’C≌△QB'M,得B'Q:PC=B'M:B'C,设 B‘Q=x, 则x:PC=(a-a):a, 解得PC=2x,
在△CB’P中,由勾股定理得PC2+PB'2=CB'2 , (2x)2+(a-x)2=a2, 解得x=a ,
∴S△AB'M=AM×B'Q=a×a=a2,
S△AB'C=S△ABC-2S△MBC-S△AB'M=a2-2×a×a-a2=a2,
∴.
13. (1)解:设直线l的函数表达式为y=kx+b(k≠0),
将A(1, ),B(4, )代入y=kx+b,
得: ,解得: ,
∴直线l的函数表达式为y=﹣ x+8
(2)解:当x=0时,y=﹣ x+8=8,
∴点D的坐标为(0,8);
当y=0时,﹣ x+8=0,
解得:x=6,
∴点C的坐标为(6,0),
∴CD=10.
分三种情况考虑(如图1所示):
①当DC=DP时,OC=OP1 ,
∴点P1的坐标为(﹣6,0);
②当CD=CP时,CP=10,
∴点P2的坐标为(﹣4,0),点P3的坐标为(16,0);
③当PC=PD时,设OP4=m,
∴(6+m)2=82+m2 ,
解得:m= ,
∴点P4的坐标为(﹣ ,0).
综上所述:点P的坐标为(﹣6,0),(﹣4,0),(16,0)或(﹣ ,0)
(3)解:过点B作直线l的垂线,交y轴于点E,如图2所示,
∵点B(4, ),点D(0,8),
∴BD= = ,
∵∠CDO=∠EDB,∠DOC=∠DBE=90°,
∴△DOC∽△DBE,
∴ ,即 ,
∴DE= ,
∴点E的坐标为(0,﹣ ).
利用待定系数法可求出直线BE的函数表达式为y= x﹣ ,
设点A′的坐标为(n, n﹣ ),
∵A′B=AB,
∴(4﹣n)2+[ ﹣( n﹣ )]2=(4﹣1)2+( ﹣ )2 ,
即n2﹣8n=0,
解得:n1=0,n2=8,
∴点A′的坐标为(0,﹣ )或(8, ).
14. (1)解:∵ ,
∴
∵
∴
∵ 是 边的中点
∴
∵
∴
∴
∴
∴
∵在 中,
∴
∵
∴
又∵
∴四边形 是矩形
∴
∵在 中,
∴
(2)解:不变
过点 作 , ,垂足分别为点 、
由(1)可得 ,
∵ ,
∴
又∵ ,
∴四边形 是矩形
∴
∵
∴ 即
又∵
∴
∴
∵
∴
(3)解:1°当 时,易证 ,即
又∵ ,D是AB的中点
∴
∴
2°当 时,易证
∵在 中,
∴设 ,则 ,
当 时,易证 ,
∴
∵
∴
∴
∴
∵
∴
∴ 解得
∴
∴
3°在BC边上截取BK=BD=5,由勾股定理得出
当 时,易证
∴设 ,则 ,
∴
∵
∴
∴
∴
∵
∴
∴ 解得
∴
∴
15. (1)解:①先设两点运动的时间是t时,△CPQ面积最小.
S△CPQ=S梯形QCOA﹣S△COP﹣S△APQ= (AQ+OC)×OA﹣ AP?AQ﹣ OC?OP
= (0.5t+6)×10﹣ ×0.5t×(10﹣t)﹣ ×6×t
= (t﹣6)2+21
∵a= >0,
∴当t=6时,S△CPQ有最小值,
那么AQ=0.5t=0.5×6=3,
∴Q点的坐标是(10,3).
②△COP和△PAQ相似,有△COP∽△PAQ和△COP∽△QAP两种情况:
(i)当△COP∽△PAQ时:
∴ = ,
∴ = ,
即t2﹣7t=0,
解得,t1=0(不合题意,舍去),t2=7.
∴t=7,
∴AQ=0.5t=0.5×7=3.5.
∴Q点的坐标是(10,3.5).
(ii)当△COP∽△QAP时:
= ,
∴ = ,
即t2+12t﹣120=0
解得:t1=﹣6+2 ,t2=﹣6﹣2 (不合题意,舍去)
∴AQ=0.5t=﹣3+ .
∴Q点的坐标是(10,﹣3+ );
(2)解:∵△COP∽△PAQ∽△CBQ,
∴ ,
即 ,
解得,t1=2,t2=18,
又∵0<t<10,
∴t=2.代入任何一个式子,可求a= .
∴AQ=at=
∴Q点的坐标是(10, ).
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
