冀教版数学七年级上册 第二章几何图形的初步认识 单元检测(解析版)
文档属性
| 名称 | 冀教版数学七年级上册 第二章几何图形的初步认识 单元检测(解析版) | 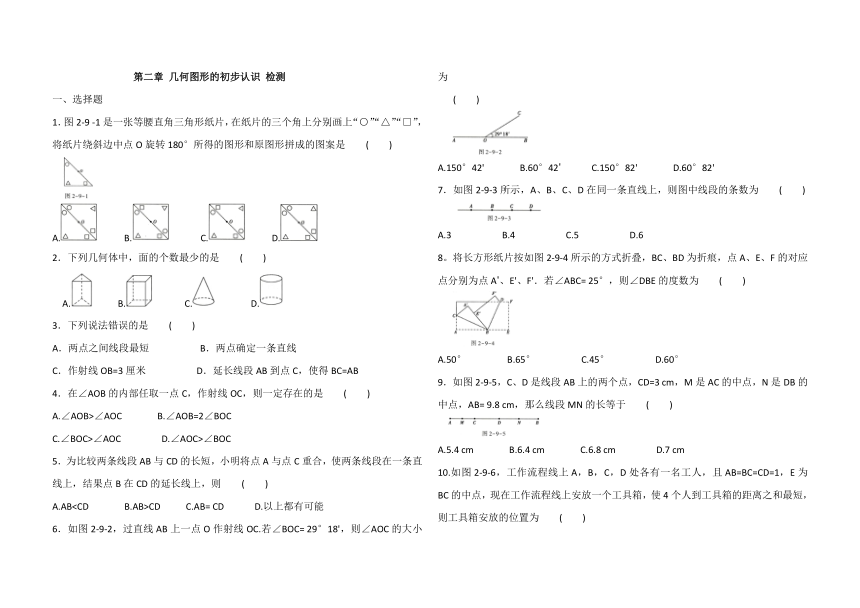 | |
| 格式 | zip | ||
| 文件大小 | 398.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-24 11:03:53 | ||
图片预览


文档简介
第二章 几何图形的初步认识 检测
一、选择题
1.图2-9 -1是一张等腰直角三角形纸片,在纸片的三个角上分别画上“○”“△”“□”,将纸片绕斜边中点O旋转180°所得的图形和原图形拼成的图案是 ( )
A. B. C. D.
2.下列几何体中,面的个数最少的是 ( )
A. B. C. D.
3.下列说法错误的是 ( )
A.两点之间线段最短 B.两点确定一条直线
C.作射线OB=3厘米 D.延长线段AB到点C,使得BC=AB
4.在∠AOB的内部任取一点C,作射线OC,则一定存在的是 ( )
A.∠AOB>∠AOC B.∠AOB=2∠BOC
C.∠BOC>∠AOC D.∠AOC>∠BOC
5.为比较两条线段AB与CD的长短,小明将点A与点C重合,使两条线段在一条直线上,结果点B在CD的延长线上,则 ( )
A.ABCD C.AB= CD D.以上都有可能
6.如图2-9-2,过直线AB上一点O作射线OC.若∠BOC= 29°18',则∠AOC的大小为
( )
A.150°42' B.60°42' C.150°82' D.60°82'
7.如图2-9-3所示,A、B、C、D在同一条直线上,则图中线段的条数为 ( )
A.3 B.4 C.5 D.6
8。将长方形纸片按如图2-9-4所示的方式折叠,BC、BD为折痕,点A、E、F的对应点分别为点A'、E'、F'.若∠ABC= 25°,则∠DBE的度数为 ( )
A.50° B.65° C.45° D.60°
9.如图2-9-5,C、D是线段AB上的两个点,CD=3 cm,M是AC的中点,N是DB的中点,AB= 9.8 cm,那么线段MN的长等于 ( )
A.5.4 cm B.6.4 cm C.6.8 cm D.7 cm
10.如图2-9-6,工作流程线上A,B,C,D处各有一名工人,且AB=BC=CD=1,E为BC的中点,现在工作流程线上安放一个工具箱,使4个人到工具箱的距离之和最短,则工具箱安放的位置为 ( )
A.线段BC上的任意一点处 B.只能是A或D处
C.只能是E处 D.线段AB或CD内的任意一点处
二、填空题
11.建筑工人砌墙时,经常在两个墙角的位置分别插一根小桩,然后拉一条直的参照线,这样做的数学道理是 .
12.如图2-9-7所示,三角形ABC绕点A旋转后得到三角形ADE,若∠BAC= 100°,∠BAD= 25°,则∠DAE= ,∠CAE= .
13.48°15 ' 48.15°.(填“>”“<”或“=”)
14.如图2-9-8,A、O、B在一条直线上,∠1=∠2.则与∠1互补的角是 .若∠1= 28°32'35",则∠1的补角= .
15.3.76° 度 分 秒;22°32'24"= 度.
16.P为线段AB上一点,且AP=AB,M是AB的中点,若PM=2 cm,则AB= cm.
17.如图2-9-9,∠AOB=90°,∠BOC=30°,OD平分∠AOC,则∠BOD=____.
18.薄薄的硬币在桌面上转动时,看上去像球,这说明了 .
三.解答题
19.计算:
(1) 90°-36°12'15"; (2) 32°17'53"+42°42'7";
(3)25°12'35"×5;(4)53°÷6.
20.如图2-9-10所示,已知AD=DB,点E是BC的中点,BE =AC=2 cm,求线段DE的长.
21.已知,A,B,O三点,如图2-9-11,按下列要求
作图:
(1)连接AB;
(2)画射线OA,BO;
(3)在线段OA,AB上分别取C,D,画直线CD.
22.已知∠AOB是一个定角,记为α,在∠AOB的内部作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1)如图2-9-12①,当α=120°,∠AOC= 40°时,求∠DOE的度数:
(2)如图2-9-12①,当射线OC在∠AOB内绕点O旋转时,∠DOE的度数是否发生变化?若变化,请说明理由;若不变,猜想∠DOE与α的关系,并证明;
(3)当射线OC在∠AOB外绕点O旋转到图2-9-12②所示的位置时,直接写出∠DOE的度数(用含n的式子表示).
答案
一、选择题
1.B
解析:根据旋转的性质可知,将纸片绕斜边中点O旋转180°所得的图形和原图形拼成的图案是选项B中的图案.
C
解析:三棱柱有5个面;长方体有6个面;圆锥有一个曲面和一个底面,共2个面:圆柱有一个侧面和两个底面,共3个面,所以面的个数最少的是圆锥,故选C.
C
解析:A.两点之间线段最短,正确,不合题意;B.两点确定一条直线,正确,不合题意;C.作射线OB=3厘米,错误,射线没有长度,符合题意;D.延长线段AB到点C,使得BC =AB.正确,不合题意,故选C.
A
解析:由叠合法可知∠AOB> ∠AOC.
B
解析:点A与点C重合,使两条线段在一条直线上,结果点B在CD的延长线上,由叠合法可知AB>CD.
A
解析: ∵∠BDC= 29°18'.∴∠AOC的度数为180° - 29°18'=150°42'.
D
解析:题图中的线段有线段AB、线段AC、线段AD、线段BC、线段BD、线段CD.共6条.故选D.
B
解析:∵一张长方形纸片沿BC、BD折叠,∴∠ABC= ∠A'BC,
∠EBD=∠E'BD、又∠ABC+ ∠A'BC+ ∠EBD+∠E'RD=180°.
∴∠ABC+∠DBE= 180°×=90°,∵∠ABC=25°,∴∠DBE= 65°.
B
解析:∵M是AC的中点,N是DB的中点,CD=3 cm,AB=9.8c.m.∴MC+DN=AC+DB= (AB-CD)=3.4 cm,
∴MN=MC+DN+CD=3.4+3=6.4 cm.
10.A设M为线段BC上任意一点,则点M到A,B,C,D的距离之和为AM+BM+CM+MD=AM+MD+BM+CM= 3+1 =4.设F为线段AB上任意一点,则点F到A,B,C,D的距离之和为AF+BF+CF+DF=AF+DF+BF+FC= 3+BF+BF+BC= 4+2BF.设N为线段CD上任意一点,同理可得点N到A,B,C,D的距离之和为4+2CN,故选A.
二、填空题
11.答案 两点确定一条直线
解析:由题意知根据两点来确定直线,所以两点确定一条直线.
12.答案100°;25°
解析:由旋转的性质可知,∠DAE=∠BAC= 100°,∠CAE=
∠BAD=25°.
13.答案 >
解析:∵48°15'= 48. 25°,48. 25°>48. 15°.∴48°15 '>48.15°.
14.答案 ∠AOD;151°27'25"
解析: ∵∠1= ∠2且∠2+ ∠AOD= 180。∴与∠1互补的角是∠AOD,
∵∠1= 28°32'35".∴∠1的补角=151°27'25".
15.答案3;45;36;22.54
解析:3.76°=3度45分36秒:22°32'24"= 22.54度.
16.答案20
解析:如图所示,∵M是AB的中点,∴AM=AB,∵P为线段AB上一点,且AP=AB.∴PM=AM-AP=AB-AB=AB=2 cm.∴AB= 20 cm.
17.答案30°
解析: 因为∠AOB=90°,∠BOC= 30°,所以∠AOC= 90°+30°=120°.
又因为OD平分∠AOC,所以∠COD=∠AOC=60°,
所以∠BOD= ∠COD-∠COB=60°-30°=30°.
18.答案 面动成体
三、解答题
19.(1)90°-36°12'15"=53°47'45".
(2) 32°17 '53"+42°42'7"= 74°59'60"= 75°.
(3) 25°12'35"×5=125°60'175"= 126°2'55".
(4)53°÷6=8°50'.
20.解析因为BE=AC=2 cm,所以AC= 10 cm,
因为点E是BC的中点,
所以BE=EC=2 cm,BC=2BE=2×2=4 cm,
则AB=AC-BC=10-4=6 cm,
又因为AD=DB,所以AB=AD+DB=AD+2AD=3AD=6 cm,
所以AD=2 cm,DB=4 cm,
所以DE=AC-AD-EC=10-2-2=6 cm(或DE= DB+BE= 4+2=6 cm).
21.解析(1)(2)(3)如图所示.
22.解析 (1)∵α=120°,∠AOC=40°,∴∠BOC=80°,
∵OD、DE分别平分∠AOC和∠BOC,
∴∠COE=∠BOC=40°,∠COD=∠AOC=20°,
∴∠DOE= ∠DOC+∠COE=60°.
(2)不变.∠DOE=α.
证明:∵∠BOC=α- ∠AOC, OD、 OE分别平分∠AOC
和∠BOC,∴∠COE= ∠BOC=α-∠AOC,∠COD= ∠AOC,
∴∠DOE= ∠COE+∠COD=α
(3) ∠DOE= ( 360°-α)= 180°-α.
一、选择题
1.图2-9 -1是一张等腰直角三角形纸片,在纸片的三个角上分别画上“○”“△”“□”,将纸片绕斜边中点O旋转180°所得的图形和原图形拼成的图案是 ( )
A. B. C. D.
2.下列几何体中,面的个数最少的是 ( )
A. B. C. D.
3.下列说法错误的是 ( )
A.两点之间线段最短 B.两点确定一条直线
C.作射线OB=3厘米 D.延长线段AB到点C,使得BC=AB
4.在∠AOB的内部任取一点C,作射线OC,则一定存在的是 ( )
A.∠AOB>∠AOC B.∠AOB=2∠BOC
C.∠BOC>∠AOC D.∠AOC>∠BOC
5.为比较两条线段AB与CD的长短,小明将点A与点C重合,使两条线段在一条直线上,结果点B在CD的延长线上,则 ( )
A.AB
6.如图2-9-2,过直线AB上一点O作射线OC.若∠BOC= 29°18',则∠AOC的大小为
( )
A.150°42' B.60°42' C.150°82' D.60°82'
7.如图2-9-3所示,A、B、C、D在同一条直线上,则图中线段的条数为 ( )
A.3 B.4 C.5 D.6
8。将长方形纸片按如图2-9-4所示的方式折叠,BC、BD为折痕,点A、E、F的对应点分别为点A'、E'、F'.若∠ABC= 25°,则∠DBE的度数为 ( )
A.50° B.65° C.45° D.60°
9.如图2-9-5,C、D是线段AB上的两个点,CD=3 cm,M是AC的中点,N是DB的中点,AB= 9.8 cm,那么线段MN的长等于 ( )
A.5.4 cm B.6.4 cm C.6.8 cm D.7 cm
10.如图2-9-6,工作流程线上A,B,C,D处各有一名工人,且AB=BC=CD=1,E为BC的中点,现在工作流程线上安放一个工具箱,使4个人到工具箱的距离之和最短,则工具箱安放的位置为 ( )
A.线段BC上的任意一点处 B.只能是A或D处
C.只能是E处 D.线段AB或CD内的任意一点处
二、填空题
11.建筑工人砌墙时,经常在两个墙角的位置分别插一根小桩,然后拉一条直的参照线,这样做的数学道理是 .
12.如图2-9-7所示,三角形ABC绕点A旋转后得到三角形ADE,若∠BAC= 100°,∠BAD= 25°,则∠DAE= ,∠CAE= .
13.48°15 ' 48.15°.(填“>”“<”或“=”)
14.如图2-9-8,A、O、B在一条直线上,∠1=∠2.则与∠1互补的角是 .若∠1= 28°32'35",则∠1的补角= .
15.3.76° 度 分 秒;22°32'24"= 度.
16.P为线段AB上一点,且AP=AB,M是AB的中点,若PM=2 cm,则AB= cm.
17.如图2-9-9,∠AOB=90°,∠BOC=30°,OD平分∠AOC,则∠BOD=____.
18.薄薄的硬币在桌面上转动时,看上去像球,这说明了 .
三.解答题
19.计算:
(1) 90°-36°12'15"; (2) 32°17'53"+42°42'7";
(3)25°12'35"×5;(4)53°÷6.
20.如图2-9-10所示,已知AD=DB,点E是BC的中点,BE =AC=2 cm,求线段DE的长.
21.已知,A,B,O三点,如图2-9-11,按下列要求
作图:
(1)连接AB;
(2)画射线OA,BO;
(3)在线段OA,AB上分别取C,D,画直线CD.
22.已知∠AOB是一个定角,记为α,在∠AOB的内部作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1)如图2-9-12①,当α=120°,∠AOC= 40°时,求∠DOE的度数:
(2)如图2-9-12①,当射线OC在∠AOB内绕点O旋转时,∠DOE的度数是否发生变化?若变化,请说明理由;若不变,猜想∠DOE与α的关系,并证明;
(3)当射线OC在∠AOB外绕点O旋转到图2-9-12②所示的位置时,直接写出∠DOE的度数(用含n的式子表示).
答案
一、选择题
1.B
解析:根据旋转的性质可知,将纸片绕斜边中点O旋转180°所得的图形和原图形拼成的图案是选项B中的图案.
C
解析:三棱柱有5个面;长方体有6个面;圆锥有一个曲面和一个底面,共2个面:圆柱有一个侧面和两个底面,共3个面,所以面的个数最少的是圆锥,故选C.
C
解析:A.两点之间线段最短,正确,不合题意;B.两点确定一条直线,正确,不合题意;C.作射线OB=3厘米,错误,射线没有长度,符合题意;D.延长线段AB到点C,使得BC =AB.正确,不合题意,故选C.
A
解析:由叠合法可知∠AOB> ∠AOC.
B
解析:点A与点C重合,使两条线段在一条直线上,结果点B在CD的延长线上,由叠合法可知AB>CD.
A
解析: ∵∠BDC= 29°18'.∴∠AOC的度数为180° - 29°18'=150°42'.
D
解析:题图中的线段有线段AB、线段AC、线段AD、线段BC、线段BD、线段CD.共6条.故选D.
B
解析:∵一张长方形纸片沿BC、BD折叠,∴∠ABC= ∠A'BC,
∠EBD=∠E'BD、又∠ABC+ ∠A'BC+ ∠EBD+∠E'RD=180°.
∴∠ABC+∠DBE= 180°×=90°,∵∠ABC=25°,∴∠DBE= 65°.
B
解析:∵M是AC的中点,N是DB的中点,CD=3 cm,AB=9.8c.m.∴MC+DN=AC+DB= (AB-CD)=3.4 cm,
∴MN=MC+DN+CD=3.4+3=6.4 cm.
10.A设M为线段BC上任意一点,则点M到A,B,C,D的距离之和为AM+BM+CM+MD=AM+MD+BM+CM= 3+1 =4.设F为线段AB上任意一点,则点F到A,B,C,D的距离之和为AF+BF+CF+DF=AF+DF+BF+FC= 3+BF+BF+BC= 4+2BF.设N为线段CD上任意一点,同理可得点N到A,B,C,D的距离之和为4+2CN,故选A.
二、填空题
11.答案 两点确定一条直线
解析:由题意知根据两点来确定直线,所以两点确定一条直线.
12.答案100°;25°
解析:由旋转的性质可知,∠DAE=∠BAC= 100°,∠CAE=
∠BAD=25°.
13.答案 >
解析:∵48°15'= 48. 25°,48. 25°>48. 15°.∴48°15 '>48.15°.
14.答案 ∠AOD;151°27'25"
解析: ∵∠1= ∠2且∠2+ ∠AOD= 180。∴与∠1互补的角是∠AOD,
∵∠1= 28°32'35".∴∠1的补角=151°27'25".
15.答案3;45;36;22.54
解析:3.76°=3度45分36秒:22°32'24"= 22.54度.
16.答案20
解析:如图所示,∵M是AB的中点,∴AM=AB,∵P为线段AB上一点,且AP=AB.∴PM=AM-AP=AB-AB=AB=2 cm.∴AB= 20 cm.
17.答案30°
解析: 因为∠AOB=90°,∠BOC= 30°,所以∠AOC= 90°+30°=120°.
又因为OD平分∠AOC,所以∠COD=∠AOC=60°,
所以∠BOD= ∠COD-∠COB=60°-30°=30°.
18.答案 面动成体
三、解答题
19.(1)90°-36°12'15"=53°47'45".
(2) 32°17 '53"+42°42'7"= 74°59'60"= 75°.
(3) 25°12'35"×5=125°60'175"= 126°2'55".
(4)53°÷6=8°50'.
20.解析因为BE=AC=2 cm,所以AC= 10 cm,
因为点E是BC的中点,
所以BE=EC=2 cm,BC=2BE=2×2=4 cm,
则AB=AC-BC=10-4=6 cm,
又因为AD=DB,所以AB=AD+DB=AD+2AD=3AD=6 cm,
所以AD=2 cm,DB=4 cm,
所以DE=AC-AD-EC=10-2-2=6 cm(或DE= DB+BE= 4+2=6 cm).
21.解析(1)(2)(3)如图所示.
22.解析 (1)∵α=120°,∠AOC=40°,∴∠BOC=80°,
∵OD、DE分别平分∠AOC和∠BOC,
∴∠COE=∠BOC=40°,∠COD=∠AOC=20°,
∴∠DOE= ∠DOC+∠COE=60°.
(2)不变.∠DOE=α.
证明:∵∠BOC=α- ∠AOC, OD、 OE分别平分∠AOC
和∠BOC,∴∠COE= ∠BOC=α-∠AOC,∠COD= ∠AOC,
∴∠DOE= ∠COE+∠COD=α
(3) ∠DOE= ( 360°-α)= 180°-α.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
