北京版五年级上册数学一课一练-3.4组合图形(含答案)
文档属性
| 名称 | 北京版五年级上册数学一课一练-3.4组合图形(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 180.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-27 10:20:58 | ||
图片预览

文档简介
五年级上册数学一课一练-3.4组合图形
一、单选题
1.将一个圆柱体削制成一个圆锥体,削去部分的体积是圆柱体积的( )
A.??????????????????????????????????????B.??????????????????????????????????????C.?2倍?????????????????????????????????????D.?不能确定
2.如图所示,长方形被分为甲、乙两部分,这两部分(??? )。
A.?周长相等,面积不相等???????????????????????????????????????B.?周长和面积都不相等 C.?周长和面积都相等??????????????????????????????????????????????D.?面积相等,周长不相等
3.某正方形园地是由边长为1米的四个小正方形组成的,现要在园地上建一个花坛(阴影部分)使花坛面积是园地面积的一半,以下图中设计不合要求的是(?? ).
A.???????????????B.???????????????C.???????????????D.?
4.等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则腰长(????? )。
A.?24厘米???????????????????????????????B.?12厘米???????????????????????????????C.?18厘米???????????????????????????????D.?36厘米
二、判断题
5.不规则图形用单位方格纸测面积,单位越小测得结果越准确
6.两个完全一样的梯形可以拼成一个平行四边形。
7.任何一个梯形都可以分成两个等高的三角形。
三、填空题
8.一座隧道的入口上部是半圆,下部是个长方形(如下图).已知长方形的长是10米,宽是5米.这个隧道横截面的周长是________米?面积是________平方米?(保留一位小数)
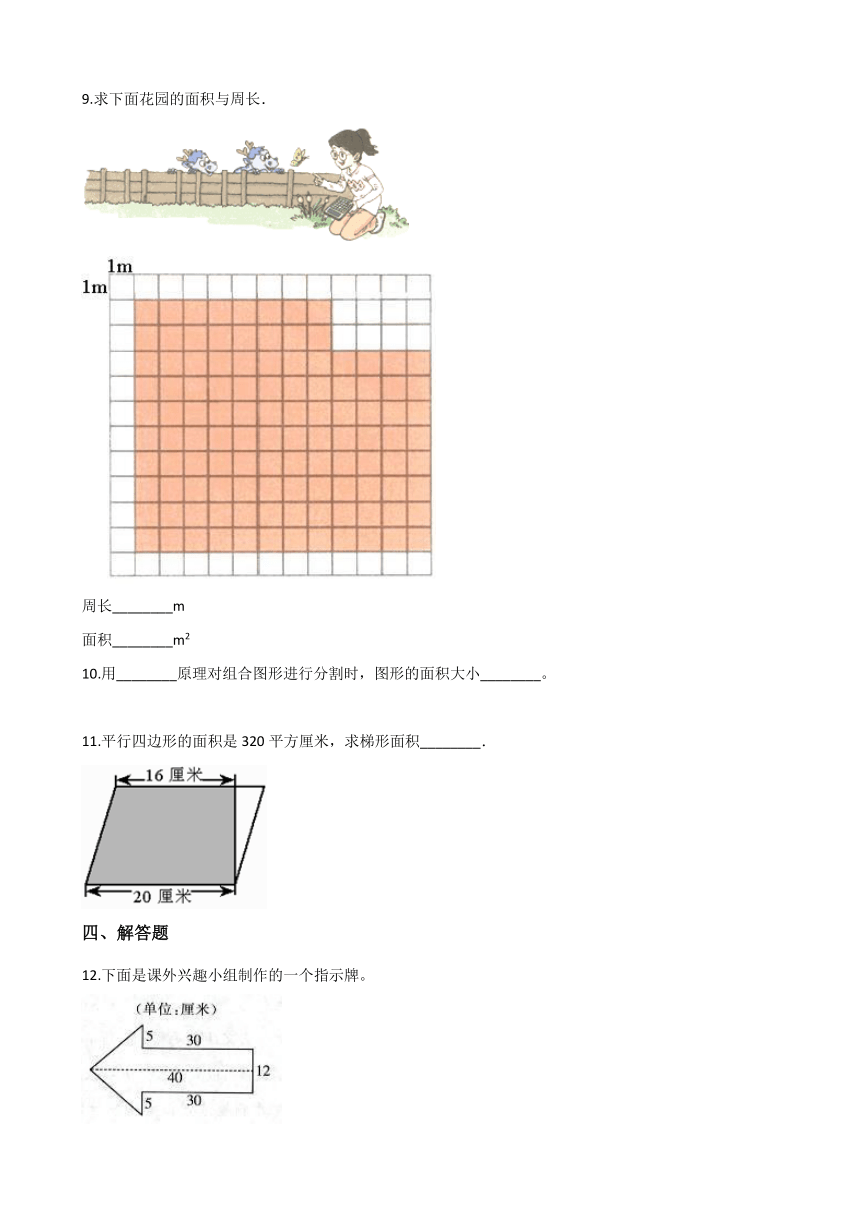
9.求下面花园的面积与周长.
周长________m
面积________m2
10.用________原理对组合图形进行分割时,图形的面积大小________。
11.平行四边形的面积是320平方厘米,求梯形面积________.
四、解答题
12.下面是课外兴趣小组制作的一个指示牌。
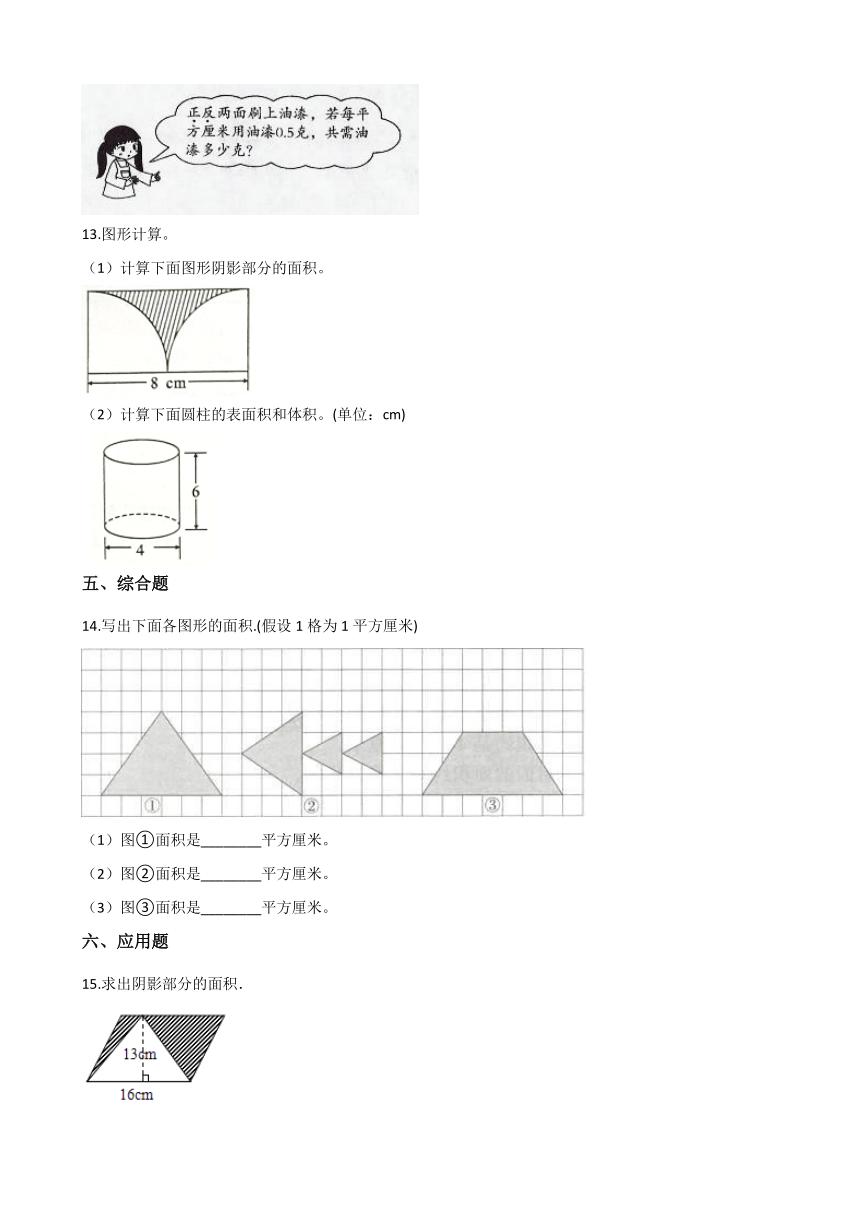
13.图形计算。
(1)计算下面图形阴影部分的面积。
(2)计算下面圆柱的表面积和体积。(单位:cm)
?
五、综合题
14.写出下面各图形的面积.(假设1格为1平方厘米)
(1)图①面积是________平方厘米。
(2)图②面积是________平方厘米。
(3)图③面积是________平方厘米。
六、应用题
15.求出阴影部分的面积.
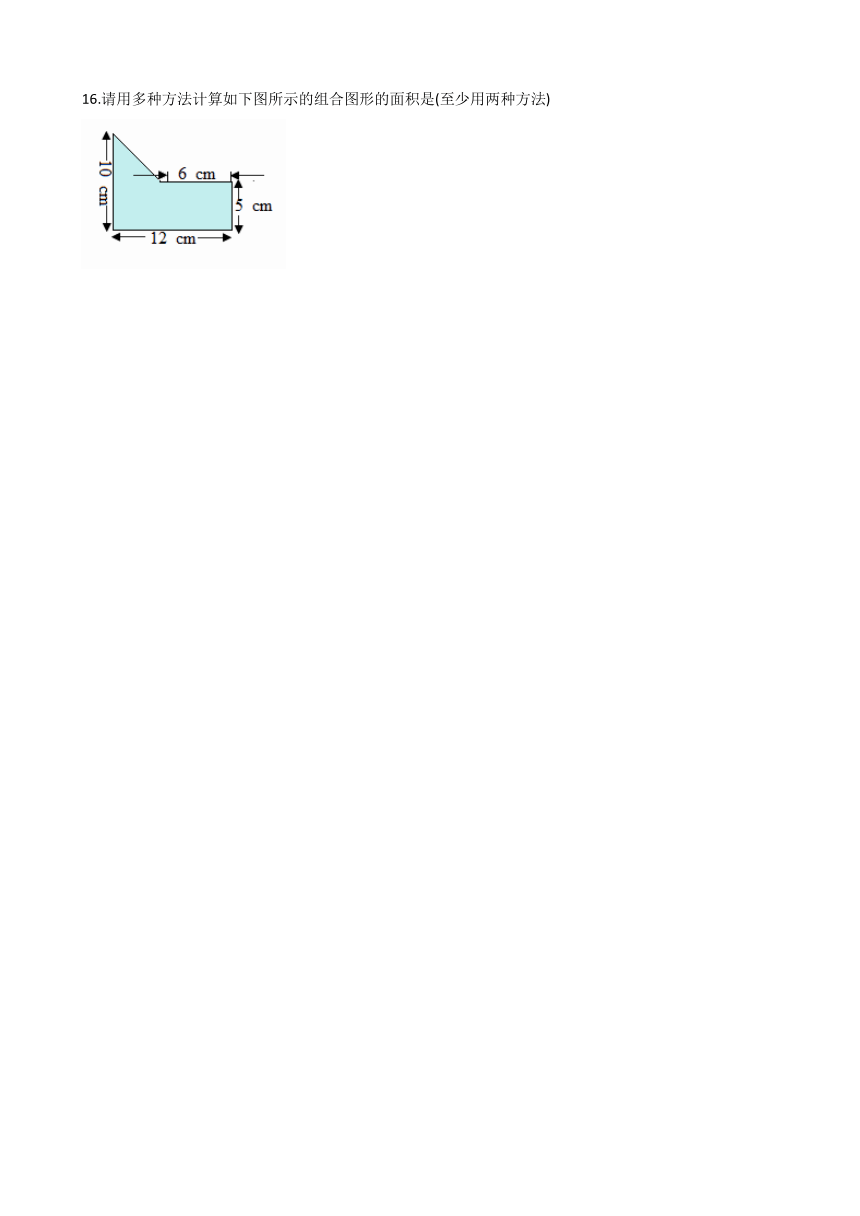
16.请用多种方法计算如下图所示的组合图形的面积是(至少用两种方法)
参考答案
一、单选题
1.【答案】 D
【解析】【解答】解:将一个圆柱体削制成一个最大的圆锥体,圆锥的体积是圆柱的, 削去部分的体积是圆柱体积的, 这里没说削成的圆锥是否最大,因此不能确定.
故选:D.
【分析】将一个圆柱体削制成一个最大的圆锥体,也就是说削成的圆锥与圆柱等底等高,圆锥的体积是圆柱的, 即削去部分的体积是圆柱体积的, 这里没说削成的圆锥是否最大,因此不能确定.
2.【答案】 A
【解析】【解答】 如图所示,长方形被分为甲、乙两部分,这两部分:周长相等,面积不相等。
故答案为:A. 【分析】观察图可知,甲、乙的周长都等于一条长+一条宽+中间的折线部分,所以周长相等; 对比面积可知,甲与乙的面积不相等,据此解答.
3.【答案】 B
【解析】【解答】解:A、阴影部分是一个三角形,三角形的底和高都与正方形的边长相等,所以三角形面积是正方形面积的一半;符合要求; B、阴影部分的面积和是2.5个小正方形的面积,大于大正方形面积的一半,不符合要求; C、阴影部分的面积之和相当于2个小正方形的面积,是大正方形面积的一半,符合要求; D、阴影部分重新组合后相当于两个小正方形的面积,是大正方形面积的一半,符合要求. 故答案为:B
【分析】根据大正方形平均分的份数结合阴影部分的大小判断出阴影部分的面积相当于几个小正方形的面积即可做出选择.
4.【答案】 B
【解析】【解答】根据题干可得,梯形的上底与下底的和为:96×2÷8=24(厘米)
梯形的腰长为:
(48-24)÷2
=24÷2
=12〔厘米〕
故选:B
【分析】根据题干,可以利用梯形的面积公式先求出上底加下底的和是多少,再利用周长求得两腰的长度。
二、判断题
5.【答案】 正确
【解析】【分析】单位越小越接近整数。
6.【答案】正确
【解析】【解答】因梯形的上底和下底平行,组成后图形的对边(上底+下底)等于(下底+上底),且平行,所以组成后的图形是平行四边形。 故答案为:正确。 【分析】因为平行四边形的对边平行且相等,两个完全一样的梯形可以以腰为公共边,其上底和下底分别对另一梯形的下底和上底,因梯形的上底和下底平行,组成后图形的对边(上底+下底)等于(下底+上底),且平行,据此解答。
7.【答案】正确
【解析】【解答】根据梯形的定义可知,有一组对边平行的四边形叫平行四边形。因为当梯形分成两个三角形时是以梯形的上底和下底为三角形的一条底边,又因为梯形的上下底是一组平行线,所以它们之间的距离是相等的,所以任何一个梯形都可以分成两个等高的三角形的说法是正确的。 故答案为:正确。 【分析】根据梯形的定义可知,有一组对边平行的四边形叫平行四边形;因为当梯形分成两个三角形时是以梯形的上底和下底为三角形的一条底边,又因为梯形的上下底是一组平行线,所以它们之间的距离是相等的,由此判断即可。
三、填空题
8.【答案】 35.7;89.3
【解析】【解答】3.14×10÷2+5×2+10 =31.4÷2+5×2+10 =15.7+10+10 =35.7(米) 3.14×(10÷2)2÷2+10×5 =3.14×52÷2+10×5 =3.14×25÷2+10×5 =78.5÷2+10×5 =39.25+50 =89.25 ≈89.3(平方米) 故答案为:35.7;89.3.
【分析】根据题意可知,要求这个隧道横截面的周长,用圆周长的一半+长+宽×2=组合图形的周长,要求组合图形的面积,用半圆的面积+长方形的面积=组合图形的面积,据此解答.
9.【答案】 44;112
【解析】【解答】解:观察图形可知:花园可补成长是12m,宽是10m的长方形与长是4m,宽是2m的长方形的差,花园的周长是:(12+10)×2=22×2=44(m);花园的面积是长是12m,宽是10m的长方形面积与长是4m,宽是2m的长方形面积的差,花园的面积是:12×10-4×2=120-8=112(m2)。 答:周长是44m;面积是112m2。 【分析】本题运用割补法,花园可补成长是12m,宽是10m的长方形与长是4m,宽是2m的长方形的差,计算周长时,花园的周长等于长是12m,宽是10m的长方形周长;再根据长方形周长=(长+宽)×2,长方形面积=长×宽,进行计算,即可解答此题。
10.【答案】出入相补;不变
【解析】【解答】用出入相补原理对组合图形进行分割时,图形的面积大小不变。 故答案为:出入相补;不变。
【分析】在计算组合图形的面积时,可利用出入相补的方法对图形进行移动、重组,而图形的面积大小不变,由此即可得出答案。
11.【答案】288平方厘米
【解析】
四、解答题
12.【答案】 解:12×30+(5+5+12)×(40-30)÷2 =360+22×10÷2 =360+110 =470(平方厘米)
470×2×0.5=470(克) 答:共需油漆470克。
【解析】【分析】指示牌的面积是左边三角形面积加上右边长方形面积。由于是两面刷漆,所以计算出面积后再乘2就是刷漆总面积,再乘每平方厘米需要油漆的重量就是需要油漆的总重量。
13.【答案】 (1)解:8÷2=4(cm) 8×4-3.14×42÷2 =32-25.12 =6.88(cm2) 答:阴影部分的面积是6.88cm2。 (2)解:表面积:3.14×(4÷2)2×2+3.14×4×6=100.48(cm2)
体积:3.14×(4÷2)2×6=75.36(cm3)
答:下面圆柱的表面积是100.48cm2和体积是75.36cm3。
【解析】【分析】(1)阴影部分的面积是长方形面积减去一个直径8cm的半圆的面积,注意长方形的宽与圆的半径相等; (2)圆柱的表面积=底面积×2+侧面积,根据圆面积公式计算底面积,用底面周长乘高求出侧面积;圆柱的体积=底面积×高,根据公式计算即可。
五、综合题
14.【答案】(1)12 (2)10 (3)15
【解析】【解答】解:(1)整格的6个,半格的12个,工12平方厘米; (2)整格的2个,半格的16个,共10平方厘米; (3)整格的11个,半格的8个,工15平方厘米. 故答案为:12;10;15
【分析】可以采用数方格的方法,先数出整格的,再数出不是整格的,把两个不是整格的合成一个整格的来判断总面积即可.
六、应用题
15.【答案】解:16×13÷2 =208÷2 =104(平方厘米) 答:阴影部分的面积是104平方厘米
【解析】【分析】根据等底等高的平行四边形的面积是三角形面积的2倍,可知图中平行四边形的面积是空白三角形面积的2倍,所以阴影部分的面积就是平行四边形面积的一半,根据平行四边形的面积公式:S=ah可求出阴影部分的面积是多少.
16.【答案】解:12×10-(6+12)×(10-5)÷2=75( )或12×5+(12-6)×(10-5)÷2=75( )。
【解析】
一、单选题
1.将一个圆柱体削制成一个圆锥体,削去部分的体积是圆柱体积的( )
A.??????????????????????????????????????B.??????????????????????????????????????C.?2倍?????????????????????????????????????D.?不能确定
2.如图所示,长方形被分为甲、乙两部分,这两部分(??? )。
A.?周长相等,面积不相等???????????????????????????????????????B.?周长和面积都不相等 C.?周长和面积都相等??????????????????????????????????????????????D.?面积相等,周长不相等
3.某正方形园地是由边长为1米的四个小正方形组成的,现要在园地上建一个花坛(阴影部分)使花坛面积是园地面积的一半,以下图中设计不合要求的是(?? ).
A.???????????????B.???????????????C.???????????????D.?
4.等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则腰长(????? )。
A.?24厘米???????????????????????????????B.?12厘米???????????????????????????????C.?18厘米???????????????????????????????D.?36厘米
二、判断题
5.不规则图形用单位方格纸测面积,单位越小测得结果越准确
6.两个完全一样的梯形可以拼成一个平行四边形。
7.任何一个梯形都可以分成两个等高的三角形。
三、填空题
8.一座隧道的入口上部是半圆,下部是个长方形(如下图).已知长方形的长是10米,宽是5米.这个隧道横截面的周长是________米?面积是________平方米?(保留一位小数)
9.求下面花园的面积与周长.
周长________m
面积________m2
10.用________原理对组合图形进行分割时,图形的面积大小________。
11.平行四边形的面积是320平方厘米,求梯形面积________.
四、解答题
12.下面是课外兴趣小组制作的一个指示牌。
13.图形计算。
(1)计算下面图形阴影部分的面积。
(2)计算下面圆柱的表面积和体积。(单位:cm)
?
五、综合题
14.写出下面各图形的面积.(假设1格为1平方厘米)
(1)图①面积是________平方厘米。
(2)图②面积是________平方厘米。
(3)图③面积是________平方厘米。
六、应用题
15.求出阴影部分的面积.
16.请用多种方法计算如下图所示的组合图形的面积是(至少用两种方法)
参考答案
一、单选题
1.【答案】 D
【解析】【解答】解:将一个圆柱体削制成一个最大的圆锥体,圆锥的体积是圆柱的, 削去部分的体积是圆柱体积的, 这里没说削成的圆锥是否最大,因此不能确定.
故选:D.
【分析】将一个圆柱体削制成一个最大的圆锥体,也就是说削成的圆锥与圆柱等底等高,圆锥的体积是圆柱的, 即削去部分的体积是圆柱体积的, 这里没说削成的圆锥是否最大,因此不能确定.
2.【答案】 A
【解析】【解答】 如图所示,长方形被分为甲、乙两部分,这两部分:周长相等,面积不相等。
故答案为:A. 【分析】观察图可知,甲、乙的周长都等于一条长+一条宽+中间的折线部分,所以周长相等; 对比面积可知,甲与乙的面积不相等,据此解答.
3.【答案】 B
【解析】【解答】解:A、阴影部分是一个三角形,三角形的底和高都与正方形的边长相等,所以三角形面积是正方形面积的一半;符合要求; B、阴影部分的面积和是2.5个小正方形的面积,大于大正方形面积的一半,不符合要求; C、阴影部分的面积之和相当于2个小正方形的面积,是大正方形面积的一半,符合要求; D、阴影部分重新组合后相当于两个小正方形的面积,是大正方形面积的一半,符合要求. 故答案为:B
【分析】根据大正方形平均分的份数结合阴影部分的大小判断出阴影部分的面积相当于几个小正方形的面积即可做出选择.
4.【答案】 B
【解析】【解答】根据题干可得,梯形的上底与下底的和为:96×2÷8=24(厘米)
梯形的腰长为:
(48-24)÷2
=24÷2
=12〔厘米〕
故选:B
【分析】根据题干,可以利用梯形的面积公式先求出上底加下底的和是多少,再利用周长求得两腰的长度。
二、判断题
5.【答案】 正确
【解析】【分析】单位越小越接近整数。
6.【答案】正确
【解析】【解答】因梯形的上底和下底平行,组成后图形的对边(上底+下底)等于(下底+上底),且平行,所以组成后的图形是平行四边形。 故答案为:正确。 【分析】因为平行四边形的对边平行且相等,两个完全一样的梯形可以以腰为公共边,其上底和下底分别对另一梯形的下底和上底,因梯形的上底和下底平行,组成后图形的对边(上底+下底)等于(下底+上底),且平行,据此解答。
7.【答案】正确
【解析】【解答】根据梯形的定义可知,有一组对边平行的四边形叫平行四边形。因为当梯形分成两个三角形时是以梯形的上底和下底为三角形的一条底边,又因为梯形的上下底是一组平行线,所以它们之间的距离是相等的,所以任何一个梯形都可以分成两个等高的三角形的说法是正确的。 故答案为:正确。 【分析】根据梯形的定义可知,有一组对边平行的四边形叫平行四边形;因为当梯形分成两个三角形时是以梯形的上底和下底为三角形的一条底边,又因为梯形的上下底是一组平行线,所以它们之间的距离是相等的,由此判断即可。
三、填空题
8.【答案】 35.7;89.3
【解析】【解答】3.14×10÷2+5×2+10 =31.4÷2+5×2+10 =15.7+10+10 =35.7(米) 3.14×(10÷2)2÷2+10×5 =3.14×52÷2+10×5 =3.14×25÷2+10×5 =78.5÷2+10×5 =39.25+50 =89.25 ≈89.3(平方米) 故答案为:35.7;89.3.
【分析】根据题意可知,要求这个隧道横截面的周长,用圆周长的一半+长+宽×2=组合图形的周长,要求组合图形的面积,用半圆的面积+长方形的面积=组合图形的面积,据此解答.
9.【答案】 44;112
【解析】【解答】解:观察图形可知:花园可补成长是12m,宽是10m的长方形与长是4m,宽是2m的长方形的差,花园的周长是:(12+10)×2=22×2=44(m);花园的面积是长是12m,宽是10m的长方形面积与长是4m,宽是2m的长方形面积的差,花园的面积是:12×10-4×2=120-8=112(m2)。 答:周长是44m;面积是112m2。 【分析】本题运用割补法,花园可补成长是12m,宽是10m的长方形与长是4m,宽是2m的长方形的差,计算周长时,花园的周长等于长是12m,宽是10m的长方形周长;再根据长方形周长=(长+宽)×2,长方形面积=长×宽,进行计算,即可解答此题。
10.【答案】出入相补;不变
【解析】【解答】用出入相补原理对组合图形进行分割时,图形的面积大小不变。 故答案为:出入相补;不变。
【分析】在计算组合图形的面积时,可利用出入相补的方法对图形进行移动、重组,而图形的面积大小不变,由此即可得出答案。
11.【答案】288平方厘米
【解析】
四、解答题
12.【答案】 解:12×30+(5+5+12)×(40-30)÷2 =360+22×10÷2 =360+110 =470(平方厘米)
470×2×0.5=470(克) 答:共需油漆470克。
【解析】【分析】指示牌的面积是左边三角形面积加上右边长方形面积。由于是两面刷漆,所以计算出面积后再乘2就是刷漆总面积,再乘每平方厘米需要油漆的重量就是需要油漆的总重量。
13.【答案】 (1)解:8÷2=4(cm) 8×4-3.14×42÷2 =32-25.12 =6.88(cm2) 答:阴影部分的面积是6.88cm2。 (2)解:表面积:3.14×(4÷2)2×2+3.14×4×6=100.48(cm2)
体积:3.14×(4÷2)2×6=75.36(cm3)
答:下面圆柱的表面积是100.48cm2和体积是75.36cm3。
【解析】【分析】(1)阴影部分的面积是长方形面积减去一个直径8cm的半圆的面积,注意长方形的宽与圆的半径相等; (2)圆柱的表面积=底面积×2+侧面积,根据圆面积公式计算底面积,用底面周长乘高求出侧面积;圆柱的体积=底面积×高,根据公式计算即可。
五、综合题
14.【答案】(1)12 (2)10 (3)15
【解析】【解答】解:(1)整格的6个,半格的12个,工12平方厘米; (2)整格的2个,半格的16个,共10平方厘米; (3)整格的11个,半格的8个,工15平方厘米. 故答案为:12;10;15
【分析】可以采用数方格的方法,先数出整格的,再数出不是整格的,把两个不是整格的合成一个整格的来判断总面积即可.
六、应用题
15.【答案】解:16×13÷2 =208÷2 =104(平方厘米) 答:阴影部分的面积是104平方厘米
【解析】【分析】根据等底等高的平行四边形的面积是三角形面积的2倍,可知图中平行四边形的面积是空白三角形面积的2倍,所以阴影部分的面积就是平行四边形面积的一半,根据平行四边形的面积公式:S=ah可求出阴影部分的面积是多少.
16.【答案】解:12×10-(6+12)×(10-5)÷2=75( )或12×5+(12-6)×(10-5)÷2=75( )。
【解析】
