北师大版九年级数学下册第一章 直角三角形的边角关系1.6 利用三角函数测高课件(共19张)
文档属性
| 名称 | 北师大版九年级数学下册第一章 直角三角形的边角关系1.6 利用三角函数测高课件(共19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-24 00:00:00 | ||
图片预览



文档简介
课件19张PPT。第一章
直角三角形的边角关系1.6 利用三角函数测高九年级数学北师版·下册教学目标1.能够设计测量方案,说明测量理由,能够综合运用直角三角形边角关系的知识解决实际问题.
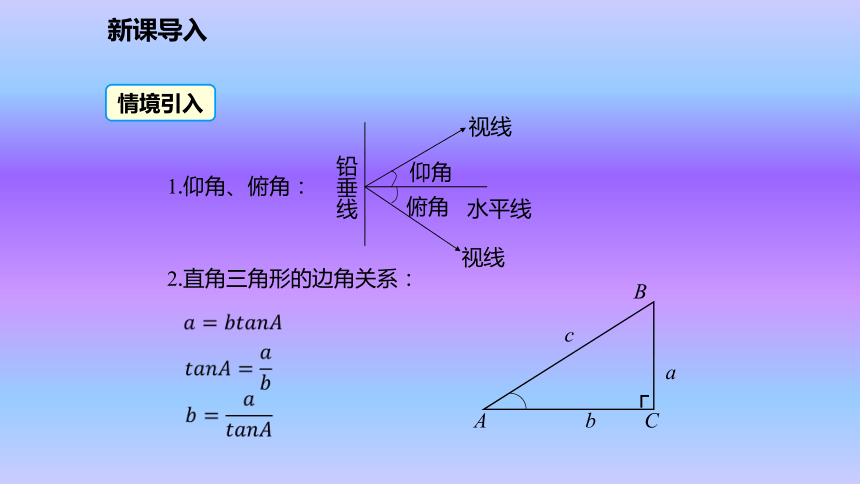
2.能对所得数据进行分析,对仪器进行调整和对测量的结果进行矫正,从而得出符合实际的结果.新课导入情境引入1.仰角、俯角:2.直角三角形的边角关系:新课导入活动课题:
利用直角三角形的边角关系测量物体的高度.
活动方式:
分组活动、全班交流研讨.
活动工具:
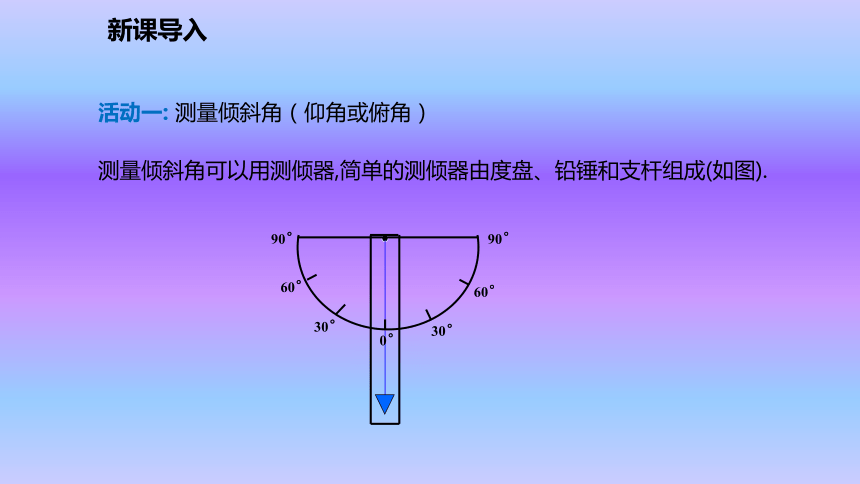
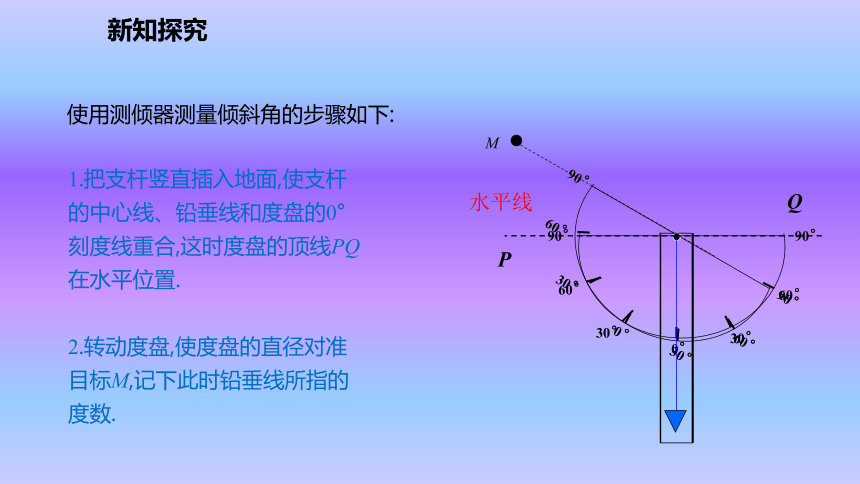
测倾器(或经纬仪、测角仪等)、皮尺等测量工具.新课导入活动一: 测量倾斜角(仰角或俯角)测量倾斜角可以用测倾器,简单的测倾器由度盘、铅锤和支杆组成(如图).新知探究水平线1.把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
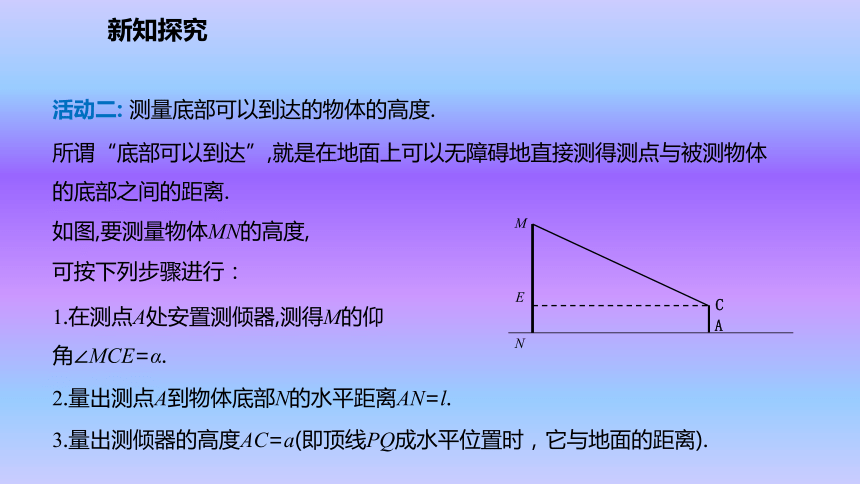
2.转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数.使用测倾器测量倾斜角的步骤如下:PQ新知探究活动二: 测量底部可以到达的物体的高度.所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.如图,要测量物体MN的高度, 1.在测点A处安置测倾器,测得M的仰角∠MCE=α.2.量出测点A到物体底部N的水平距离AN=l.3.量出测倾器的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).CAENM可按下列步骤进行:新知探究根据刚才测量的数据,你能求出物体MN的高度吗?说说你的理由.能.理由:在Rt△MCE中,
ME=EC·tanα=AN·tanα
=l·tanα,
MN=ME+EN=ME+AC=l·tanα+ a.aCAENMl议一议:新知探究所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体的底部之间的距离.要测量物体MN的高度,使用测倾器测一次仰角够吗?aECA活动三: 测量底部不可以到达的物体的高度.新知探究要测量物体MN的高度,测一次仰角是不够的.abECADB还需哪些条件?测量哪些数据?议一议:新知探究如图,要测量物体MN的高度,可以按下列步骤进行:1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α.2.在测点A与物体之间的B处安置测倾器(A,B与N在一条直线上,且A,B之间的距离可以直接测得), 测得此时M的仰角∠MDE=β.3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.根据测量数据,你能求出物体MN的高度吗?
说说你的理由.新知探究过程:根据测量数据,物体MN的高度计算过程为:在Rt△ MDE中,ED= ,
在Rt△MCE中,EC= ,
EC-ED= - =b,
课堂小结本课主要学习测量物体的高度的方法:1.测量底部可以到达的物体的高度.2.测量底部不可以到达的物体的高度.3.目前我们学习的测量物体高度的方法有相似法、全等法、三角函数法.规律方法:
根据实际情况,选择测量方法,画出几何图形,构造直角三角形,灵活运用三角函数的定义结合勾股定理等有关知识是进行解题的关键.课堂小测1.如图,在Rt△ABC中,∠C=90°, AM是BC边上的中线,则tan B的值为__________.解析:首先利用已知的正弦值,得出AC与MC之间的比值关系为4:3,再利用AM是BC的中线这一条件,求出AC与BC的比值,即可解题.?课堂小测2.如图,一艘船向正北航行,在A处看到灯塔S在船的北偏东30°的方向上,航行12海里到达B点,在B处看到灯塔S在船的北偏东60°的方向上,此船继续沿正北方向航行的过程中距灯塔S的最近距离是 海里(不作近似计算).解析:过S点作AB的垂线,交AB与N点,已知AB=12,利用等腰三角形的性质,可知BS=12,再利用30°所对的直角边等于斜边一半的原理,得出BN=6,进而利用勾股定理求出NS即可.N课堂小测?课堂小测∵AD平分∠BAC,解: 在Rt△ABC中,∴在Rt△ACD中,∠CAD=30°.∵∠B=30°,课堂小测(参考数据: )4.小明家所在居民楼的对面有一座大厦AB,AB=80米.为测量居民楼与这座大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.(结果保留整数)课堂小测∵AD+BD = AB,
∴在Rt△BCD中,tan48°= 解得x≈43.
答:小明家所在居民楼与大厦的距离CD大约是43米. , 则则
2.能对所得数据进行分析,对仪器进行调整和对测量的结果进行矫正,从而得出符合实际的结果.新课导入情境引入1.仰角、俯角:2.直角三角形的边角关系:新课导入活动课题:
利用直角三角形的边角关系测量物体的高度.
活动方式:
分组活动、全班交流研讨.
活动工具:
测倾器(或经纬仪、测角仪等)、皮尺等测量工具.新课导入活动一: 测量倾斜角(仰角或俯角)测量倾斜角可以用测倾器,简单的测倾器由度盘、铅锤和支杆组成(如图).新知探究水平线1.把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
2.转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数.使用测倾器测量倾斜角的步骤如下:PQ新知探究活动二: 测量底部可以到达的物体的高度.所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.如图,要测量物体MN的高度, 1.在测点A处安置测倾器,测得M的仰角∠MCE=α.2.量出测点A到物体底部N的水平距离AN=l.3.量出测倾器的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).CAENM可按下列步骤进行:新知探究根据刚才测量的数据,你能求出物体MN的高度吗?说说你的理由.能.理由:在Rt△MCE中,
ME=EC·tanα=AN·tanα
=l·tanα,
MN=ME+EN=ME+AC=l·tanα+ a.aCAENMl议一议:新知探究所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体的底部之间的距离.要测量物体MN的高度,使用测倾器测一次仰角够吗?aECA活动三: 测量底部不可以到达的物体的高度.新知探究要测量物体MN的高度,测一次仰角是不够的.abECADB还需哪些条件?测量哪些数据?议一议:新知探究如图,要测量物体MN的高度,可以按下列步骤进行:1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α.2.在测点A与物体之间的B处安置测倾器(A,B与N在一条直线上,且A,B之间的距离可以直接测得), 测得此时M的仰角∠MDE=β.3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.根据测量数据,你能求出物体MN的高度吗?
说说你的理由.新知探究过程:根据测量数据,物体MN的高度计算过程为:在Rt△ MDE中,ED= ,
在Rt△MCE中,EC= ,
EC-ED= - =b,
课堂小结本课主要学习测量物体的高度的方法:1.测量底部可以到达的物体的高度.2.测量底部不可以到达的物体的高度.3.目前我们学习的测量物体高度的方法有相似法、全等法、三角函数法.规律方法:
根据实际情况,选择测量方法,画出几何图形,构造直角三角形,灵活运用三角函数的定义结合勾股定理等有关知识是进行解题的关键.课堂小测1.如图,在Rt△ABC中,∠C=90°, AM是BC边上的中线,则tan B的值为__________.解析:首先利用已知的正弦值,得出AC与MC之间的比值关系为4:3,再利用AM是BC的中线这一条件,求出AC与BC的比值,即可解题.?课堂小测2.如图,一艘船向正北航行,在A处看到灯塔S在船的北偏东30°的方向上,航行12海里到达B点,在B处看到灯塔S在船的北偏东60°的方向上,此船继续沿正北方向航行的过程中距灯塔S的最近距离是 海里(不作近似计算).解析:过S点作AB的垂线,交AB与N点,已知AB=12,利用等腰三角形的性质,可知BS=12,再利用30°所对的直角边等于斜边一半的原理,得出BN=6,进而利用勾股定理求出NS即可.N课堂小测?课堂小测∵AD平分∠BAC,解: 在Rt△ABC中,∴在Rt△ACD中,∠CAD=30°.∵∠B=30°,课堂小测(参考数据: )4.小明家所在居民楼的对面有一座大厦AB,AB=80米.为测量居民楼与这座大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.(结果保留整数)课堂小测∵AD+BD = AB,
∴在Rt△BCD中,tan48°= 解得x≈43.
答:小明家所在居民楼与大厦的距离CD大约是43米. , 则则
