冀教版数学五年级下册5.4《解决问题》(课件20张ppt)
文档属性
| 名称 | 冀教版数学五年级下册5.4《解决问题》(课件20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 378.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 18:24:21 | ||
图片预览







文档简介
课件20张PPT。小学数学冀教版五年级下册第五单元第4课回忆长方体和正方体体积的计算方法: 导入新课 导入新课1立方米=1000立方分米1立方分米=1000立方厘米1立方米=1000立方分米=1000000立方厘米回忆体积单位之间的换算:长方体和正方体的体积解决问题 导入新课 新课学习 李大伯计划挖一个长是2米,宽是1.6米,深是1.5米的地窖。要挖出多少立方米的土?生活中,计量沙、土、石子等的体积时,常常把“立方米”简称为“方”。 分析:地窖是呈长方体状的,地窖的长、宽、深相当于长方体的长、宽、高,直接带入公式计算结果即可。 新课学习2×1.6×1.5=4.8(立方米)
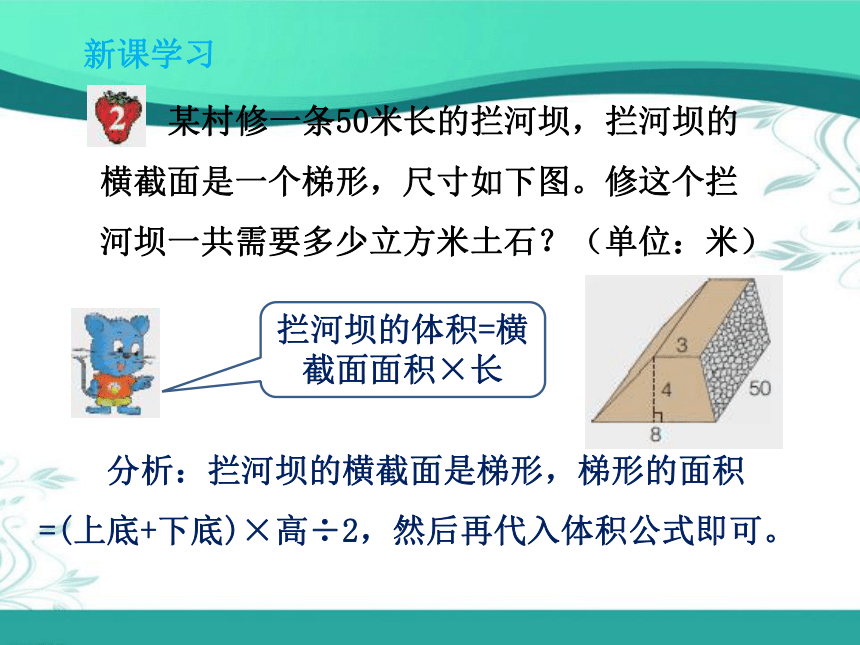
答:要挖出4.8立方米的土。 李大伯计划挖一个长是2米,宽是1.6米,深是1.5米的地窖。要挖出多少立方米的土? 新课学习 某村修一条50米长的拦河坝,拦河坝的横截面是一个梯形,尺寸如下图。修这个拦河坝一共需要多少立方米土石?(单位:米)拦河坝的体积=横截面面积×长 分析:拦河坝的横截面是梯形,梯形的面积=(上底+下底)×高÷2,然后再代入体积公式即可。 新课学习 某村修一条50米长的拦河坝,拦河坝的横截面是一个梯形,尺寸如下图。修这个拦河坝一共需要多少立方米土石?(单位:米)S =(3+8)×4÷2
=11×4÷2
=22(米)
V = Sh = 22×50 = 1100(立方米)
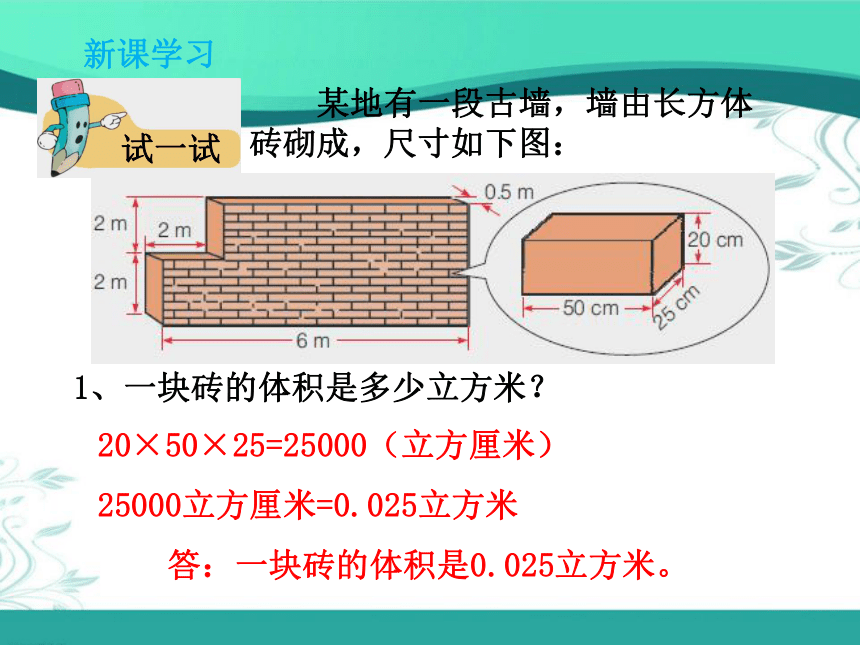
答:一共需要1100立方米的土石。 新课学习 某地有一段古墙,墙由长方体砖砌成,尺寸如下图:1、一块砖的体积是多少立方米?20×50×25=25000(立方厘米)
25000立方厘米=0.025立方米
答:一块砖的体积是0.025立方米。 新课学习2、空缺部分的体积是多少?需要多少块砖才 能补齐?2×2×0.5=2(立方米)
2÷0.025=80(块)
答:空缺部分的体积是2立方米,
需要80块砖。 新课学习3、古墙的体积是多少?一共有多少块砖?6×(2+2)×0.5-2=10(立方米)
10÷0.025=400(块)
答:古墙的体积是10立方米,
一共有400块砖。(古墙的体积=长方体体积-空缺部分体积) 新课学习3、古墙的体积是多少?一共有多少块砖?6×2×0.5+(6-2)×2×0.5=10(立方米)
10÷0.025=400(块)
答:古墙的体积是10立方米,
一共有400块砖。(古墙的体积=上下两个长方体体积之和) 新课学习3、古墙的体积是多少?一共有多少块砖?2×2×0.5+(6-2)×(2+2)×0.5=10(立方米)
10÷0.025=400(块)
答:古墙的体积是10立方米,
一共有400块砖。(古墙的体积=左右两个长方体体积之和) 结论总结解决问题的步骤:
1、找出题中的长方体或正方体;
2、找出长方体的 长、宽、高或 正方体的棱长;
3、代入体积公式。 结论总结求组合图形体积的方法:
1、把组合图形分解或补全;
2、分解:把组合图形分解成规则的正方体或长方体,求体积之和;
3、补全:求出补全后的规则的长方体或正方体的体积,减去补充部分的体积。 课堂练习练一练1、下面是一根混凝土的铁路轨枕,求它的体积。18m=1800cm
S=(16+28)×16÷2=352(cm2)
V=Sh=352×1800=633600(cm2)
633600cm2=0.6336m2
答:轨枕的体积是0.6336m2。 课堂练习2、下面是一个喂马的木槽,尺寸如下图:(单位:米) 如果把这个木槽中装满饲料,饲料的体积是多少?(木槽厚度不计)S=(0.5+0.36)×0.32÷2=0.1376(平方米)
V= Sh =0.1376×1.5=0.2064(平方米)
答:饲料的体积是0.2064平方米。 作业布置课本66页练一练第3、4、5题
69页练习第3、4题 板书设计解决问题
1、拦河坝的体积=横截面面积×长
2、解决问题的步骤:
找出长方体的 长、宽、高或正方体的棱长代入体积公式。
3、求组合图形体积的方法:分解或补全。谢谢!
答:要挖出4.8立方米的土。 李大伯计划挖一个长是2米,宽是1.6米,深是1.5米的地窖。要挖出多少立方米的土? 新课学习 某村修一条50米长的拦河坝,拦河坝的横截面是一个梯形,尺寸如下图。修这个拦河坝一共需要多少立方米土石?(单位:米)拦河坝的体积=横截面面积×长 分析:拦河坝的横截面是梯形,梯形的面积=(上底+下底)×高÷2,然后再代入体积公式即可。 新课学习 某村修一条50米长的拦河坝,拦河坝的横截面是一个梯形,尺寸如下图。修这个拦河坝一共需要多少立方米土石?(单位:米)S =(3+8)×4÷2
=11×4÷2
=22(米)
V = Sh = 22×50 = 1100(立方米)
答:一共需要1100立方米的土石。 新课学习 某地有一段古墙,墙由长方体砖砌成,尺寸如下图:1、一块砖的体积是多少立方米?20×50×25=25000(立方厘米)
25000立方厘米=0.025立方米
答:一块砖的体积是0.025立方米。 新课学习2、空缺部分的体积是多少?需要多少块砖才 能补齐?2×2×0.5=2(立方米)
2÷0.025=80(块)
答:空缺部分的体积是2立方米,
需要80块砖。 新课学习3、古墙的体积是多少?一共有多少块砖?6×(2+2)×0.5-2=10(立方米)
10÷0.025=400(块)
答:古墙的体积是10立方米,
一共有400块砖。(古墙的体积=长方体体积-空缺部分体积) 新课学习3、古墙的体积是多少?一共有多少块砖?6×2×0.5+(6-2)×2×0.5=10(立方米)
10÷0.025=400(块)
答:古墙的体积是10立方米,
一共有400块砖。(古墙的体积=上下两个长方体体积之和) 新课学习3、古墙的体积是多少?一共有多少块砖?2×2×0.5+(6-2)×(2+2)×0.5=10(立方米)
10÷0.025=400(块)
答:古墙的体积是10立方米,
一共有400块砖。(古墙的体积=左右两个长方体体积之和) 结论总结解决问题的步骤:
1、找出题中的长方体或正方体;
2、找出长方体的 长、宽、高或 正方体的棱长;
3、代入体积公式。 结论总结求组合图形体积的方法:
1、把组合图形分解或补全;
2、分解:把组合图形分解成规则的正方体或长方体,求体积之和;
3、补全:求出补全后的规则的长方体或正方体的体积,减去补充部分的体积。 课堂练习练一练1、下面是一根混凝土的铁路轨枕,求它的体积。18m=1800cm
S=(16+28)×16÷2=352(cm2)
V=Sh=352×1800=633600(cm2)
633600cm2=0.6336m2
答:轨枕的体积是0.6336m2。 课堂练习2、下面是一个喂马的木槽,尺寸如下图:(单位:米) 如果把这个木槽中装满饲料,饲料的体积是多少?(木槽厚度不计)S=(0.5+0.36)×0.32÷2=0.1376(平方米)
V= Sh =0.1376×1.5=0.2064(平方米)
答:饲料的体积是0.2064平方米。 作业布置课本66页练一练第3、4、5题
69页练习第3、4题 板书设计解决问题
1、拦河坝的体积=横截面面积×长
2、解决问题的步骤:
找出长方体的 长、宽、高或正方体的棱长代入体积公式。
3、求组合图形体积的方法:分解或补全。谢谢!
