人教A版高中数学必修三 课件:1.3 算法案例 :25张PPT
文档属性
| 名称 | 人教A版高中数学必修三 课件:1.3 算法案例 :25张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 07:18:06 | ||
图片预览








文档简介
课件25张PPT。1.3 算法案例[目标导航]新知导学·素养养成1.求两个正整数的最大公约数的算法
(1)辗转相除法(欧几里得算法)的算法步骤:
第一步,给定 .
第二步,计算 .
第三步, .
第四步,若r=0,则m,n的最大公约数等于 ;否则返回 .
(2)更相减损术的算法步骤
第一步,任意给定两个正整数,判断它们是否都是 .若是, ;若不是,执行 .
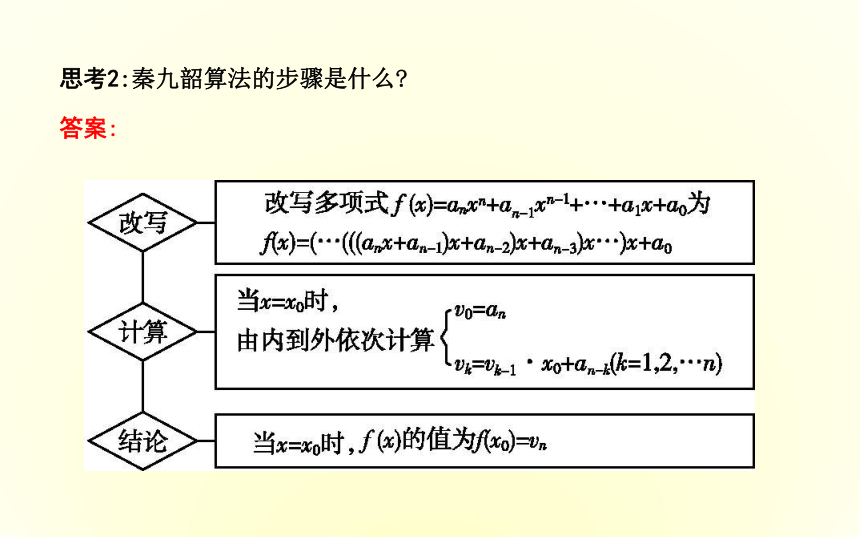
第二步,以 的数减去 的数,接着把所得的差与 的数比较,并以大数减小数,继续这个操作,直到所得的数 为止,则这个数(等数)或这个数与约简的数的乘积就是所求的最大公约数.两个正整数m,nm除以n所得的余数rm=n,n=rm第二步偶数用2约简第二步较大较小较小相等思考1:辗转相除法与更相减损术有何异同?答案:2.秦九韶算法
把一个n次多项式f(x)=anxn+an-1xn-1+…+a1x+a0改写成如下形式:
f(x)=anxn+an-1xn-1+…+a1x+a0
=(anxn-1+an-1xn-2+…+a1)x+a0
=((anxn-2+an-1xn-3+…+a2)x+a1)x+a0
=…
=(…((anx+an-1)x+an-2)x+…+a1)x+a0.
求多项式的值时,首先计算最内层括号内一次多项式的值,即v1=anx+an-1,
然后由内向外逐层计算一次多项式的值,即
v2=v1x+an-2,v3=v2x+an-3,…vn=vn-1x+a0.
这样,求n次多项式f(x)的值就转化为求n个一次多项式的值.思考2:秦九韶算法的步骤是什么?答案:3.进位制
(1)概念:进位制是为了 而约定的记数系统,“满几进一”就是几进制,几进制的基数就是 .
(2)不同进位制之间的互化:①k进制化为十进制的方法:
anan-1…a1a0(k)= (an,an-1,…,a1,a0∈N,
0(1)二进制:①只使用0和1两个数字;②满二进一,如1+1=10.
(2)八进制:①使用0,1,2,3,4,5,6,7八个不同的数字;②满八进一,如7+1=10.
(3)十六进制:①使用0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F这十六个不同的数码,其中A,B,C,D,E,F分别代表十进制中的10,11,12,13,14,15;②满十六进一,如F+1=2+E=10.课堂探究·素养提升题型一 求最大公约数
[例1] 分别用辗转相除法和更相减损术求779与209的最大公约数.解:法一 辗转相除法:
779=209×3+152,
209=152×1+57,
152=57×2+38,
57=38×1+19,
38=19×2.
所以,779与209的最大公约数为19.法二 更相减损术法:
779-209=570,570-209=361,361-209=152,209-152=57,152-57=95,
95-57=38,57-38=19,38-19=19.
所以779和209的最大公约数为19.方法技巧求两个正整数的最大公约数的问题,可以用辗转相除法,也可以用更相减损术.即时训练1-1:(2019·安徽省屯溪第一中学月考)数612和486的最大公约数是( )
(A)12 (B)14 (C)16 (D)18解析:612-486=126,486-126=360,360-126=234,234-126=108,
126-108=18,108-18=90,90-18=72,72-18=54,54-18=36,36-18=18.
因此612与486的最大公约数是18.故选D.解:f(x)=(((((6x+5)x+4)x+3)x+2)x+1)x,
当x=2时,有
v0=6,
v1=6×2+5=17,
v2=17×2+4=38,
v3=38×2+3=79,
v4=79×2+2=160,
v5=160×2+1=321,
v6=321×2=642,
故当x=2时,多项式f(x)=6x6+5x5+4x4+3x3+2x2+x的值为642.题型二 秦九韶算法
[例2] 用秦九韶算法求多项式f(x)=6x6+5x5+4x4+3x3+2x2+x,当x=2时的值.方法技巧在运用秦九韶算法进行计算时,应注意每一步的运算结果,像这种一环扣一环的运算,如果错一步,那么下一步,一直到最后一步就会全部算错,在计算这种题时应格外小心.即时训练2-1:(2019·福建仙游一中月考)利用秦九韶算法计算f(x)=x5+4x4-3x2+x+5,x=2,v3等于( )
(A)43 (B)19 (C)12 (D)6解析:由题意可知:f(x)=(((x+4)x-3)x+1)x+5,
当x=2时,v0=1,v1=v0x+4=1×2+4=6,
v2=v1x-3=6×2-3=9,v3=v2x+1=9×2+1=19.故选B.解:(1)101 111 011(2)=1×28+0×27+1×26+1×25+1×24+1×23+0×22+
1×21+1×20=379.
(2)235(7)=2×72+3×71+5×70=124.题型三 进位制
[例3] (1)将101 111 011(2)转化为十进制数;
(2)将235(7)转化为十进制数;解:(3)因为137=3×62+4×6+5,
所以137=345(6).(3)将137转化为六进制数;解:(4)53(8)=5×81+3×80=43.
所以53(8)=101 011(2).(4)将53(8)转化为二进制数.方法技巧k进制数化为十进制数的步骤
(1)把k进制数写成不同数位上的数字与k的幂的乘积之和的形式.
(2)按十进制数的运算规则采用短除法运算出结果.即时训练3-1:(1)(2019·安徽屯溪一中学月考)729化成六进制,其结果是( )
(A)3 321(6) (B)3 223(6)
(C)3 213(6) (D)3 123(6)(1)解析:由题得
则729=3 213(6).故选C.(2)若六进制数13m502(6)化为十进制数等于12 710,求数字m的值.(2)解:因为13m502(6)
=1×65+3×64+m×63+5×62+0×61+2×60
=216m+11 846,
令216m+11 846=12 710,
所以m=4.课堂达标解析:f(x)=(((((3x+4)x+5)x+6)x+7)x+8)x+1,所以需要进行6次乘法和6次加法.1.用秦九韶算法计算多项式f(x)=3x6+4x5+5x4+6x3+7x2+8x+1.当x=0.4时的值时,需要做乘法和加法的次数分别是( )
(A)6,6 (B)5,6 (C)5,5 (D)6,5A2.(2019·河南林州一中月考)用秦九韶算法求多项式f(x)=12+35x-8x2+
79x3+6x4+5x5+3x6在x=-4时的值时,其中v4的值为( )
(A)-57 (B)124 (C)-845 (D)220解析:f(x)=(((((3x+5)x+6)x+79)x-8)x+35)x+12
当x=-4时v4=(((3x+5)x+6)x+79)x-8=220.故选D.D3.(2019·河南省开封一中月考)下列各数中与1 010(4)相等的数是( )
(A)76(9) (B)103(8)
(C)1 000 100(2) (D)2 111(3)解析:1 010(4)=1×43+0×42+1×41+0×40=68(10),
1 000 100(2)=1×26+1×22=68(10).故选C.C4.用辗转相除法和更相减损术求1 515与600的最大公约数,需要运算的次数分别为( )
(A)4,15 (B)5,14 (C)5,13 (D)4,12解析:辗转相除法:1 515=600×2+315;600=315×1+285,315=285×1
+30,285=30×9+15,30=15×2,故最大公约数为15,且需计算5次.用更相减损术法:1 515-600=915,915-600=315,600-315=285,315-285=30,
285-30=255,255-30=225,225-30=195,195-30=165,165-30=135,135-30=105,105-30=75,75-30=45,45-30=15,30-15=15,故最大公约数为15,且需计算14次.故选B.B
(1)辗转相除法(欧几里得算法)的算法步骤:
第一步,给定 .
第二步,计算 .
第三步, .
第四步,若r=0,则m,n的最大公约数等于 ;否则返回 .
(2)更相减损术的算法步骤
第一步,任意给定两个正整数,判断它们是否都是 .若是, ;若不是,执行 .
第二步,以 的数减去 的数,接着把所得的差与 的数比较,并以大数减小数,继续这个操作,直到所得的数 为止,则这个数(等数)或这个数与约简的数的乘积就是所求的最大公约数.两个正整数m,nm除以n所得的余数rm=n,n=rm第二步偶数用2约简第二步较大较小较小相等思考1:辗转相除法与更相减损术有何异同?答案:2.秦九韶算法
把一个n次多项式f(x)=anxn+an-1xn-1+…+a1x+a0改写成如下形式:
f(x)=anxn+an-1xn-1+…+a1x+a0
=(anxn-1+an-1xn-2+…+a1)x+a0
=((anxn-2+an-1xn-3+…+a2)x+a1)x+a0
=…
=(…((anx+an-1)x+an-2)x+…+a1)x+a0.
求多项式的值时,首先计算最内层括号内一次多项式的值,即v1=anx+an-1,
然后由内向外逐层计算一次多项式的值,即
v2=v1x+an-2,v3=v2x+an-3,…vn=vn-1x+a0.
这样,求n次多项式f(x)的值就转化为求n个一次多项式的值.思考2:秦九韶算法的步骤是什么?答案:3.进位制
(1)概念:进位制是为了 而约定的记数系统,“满几进一”就是几进制,几进制的基数就是 .
(2)不同进位制之间的互化:①k进制化为十进制的方法:
anan-1…a1a0(k)= (an,an-1,…,a1,a0∈N,
0
(2)八进制:①使用0,1,2,3,4,5,6,7八个不同的数字;②满八进一,如7+1=10.
(3)十六进制:①使用0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F这十六个不同的数码,其中A,B,C,D,E,F分别代表十进制中的10,11,12,13,14,15;②满十六进一,如F+1=2+E=10.课堂探究·素养提升题型一 求最大公约数
[例1] 分别用辗转相除法和更相减损术求779与209的最大公约数.解:法一 辗转相除法:
779=209×3+152,
209=152×1+57,
152=57×2+38,
57=38×1+19,
38=19×2.
所以,779与209的最大公约数为19.法二 更相减损术法:
779-209=570,570-209=361,361-209=152,209-152=57,152-57=95,
95-57=38,57-38=19,38-19=19.
所以779和209的最大公约数为19.方法技巧求两个正整数的最大公约数的问题,可以用辗转相除法,也可以用更相减损术.即时训练1-1:(2019·安徽省屯溪第一中学月考)数612和486的最大公约数是( )
(A)12 (B)14 (C)16 (D)18解析:612-486=126,486-126=360,360-126=234,234-126=108,
126-108=18,108-18=90,90-18=72,72-18=54,54-18=36,36-18=18.
因此612与486的最大公约数是18.故选D.解:f(x)=(((((6x+5)x+4)x+3)x+2)x+1)x,
当x=2时,有
v0=6,
v1=6×2+5=17,
v2=17×2+4=38,
v3=38×2+3=79,
v4=79×2+2=160,
v5=160×2+1=321,
v6=321×2=642,
故当x=2时,多项式f(x)=6x6+5x5+4x4+3x3+2x2+x的值为642.题型二 秦九韶算法
[例2] 用秦九韶算法求多项式f(x)=6x6+5x5+4x4+3x3+2x2+x,当x=2时的值.方法技巧在运用秦九韶算法进行计算时,应注意每一步的运算结果,像这种一环扣一环的运算,如果错一步,那么下一步,一直到最后一步就会全部算错,在计算这种题时应格外小心.即时训练2-1:(2019·福建仙游一中月考)利用秦九韶算法计算f(x)=x5+4x4-3x2+x+5,x=2,v3等于( )
(A)43 (B)19 (C)12 (D)6解析:由题意可知:f(x)=(((x+4)x-3)x+1)x+5,
当x=2时,v0=1,v1=v0x+4=1×2+4=6,
v2=v1x-3=6×2-3=9,v3=v2x+1=9×2+1=19.故选B.解:(1)101 111 011(2)=1×28+0×27+1×26+1×25+1×24+1×23+0×22+
1×21+1×20=379.
(2)235(7)=2×72+3×71+5×70=124.题型三 进位制
[例3] (1)将101 111 011(2)转化为十进制数;
(2)将235(7)转化为十进制数;解:(3)因为137=3×62+4×6+5,
所以137=345(6).(3)将137转化为六进制数;解:(4)53(8)=5×81+3×80=43.
所以53(8)=101 011(2).(4)将53(8)转化为二进制数.方法技巧k进制数化为十进制数的步骤
(1)把k进制数写成不同数位上的数字与k的幂的乘积之和的形式.
(2)按十进制数的运算规则采用短除法运算出结果.即时训练3-1:(1)(2019·安徽屯溪一中学月考)729化成六进制,其结果是( )
(A)3 321(6) (B)3 223(6)
(C)3 213(6) (D)3 123(6)(1)解析:由题得
则729=3 213(6).故选C.(2)若六进制数13m502(6)化为十进制数等于12 710,求数字m的值.(2)解:因为13m502(6)
=1×65+3×64+m×63+5×62+0×61+2×60
=216m+11 846,
令216m+11 846=12 710,
所以m=4.课堂达标解析:f(x)=(((((3x+4)x+5)x+6)x+7)x+8)x+1,所以需要进行6次乘法和6次加法.1.用秦九韶算法计算多项式f(x)=3x6+4x5+5x4+6x3+7x2+8x+1.当x=0.4时的值时,需要做乘法和加法的次数分别是( )
(A)6,6 (B)5,6 (C)5,5 (D)6,5A2.(2019·河南林州一中月考)用秦九韶算法求多项式f(x)=12+35x-8x2+
79x3+6x4+5x5+3x6在x=-4时的值时,其中v4的值为( )
(A)-57 (B)124 (C)-845 (D)220解析:f(x)=(((((3x+5)x+6)x+79)x-8)x+35)x+12
当x=-4时v4=(((3x+5)x+6)x+79)x-8=220.故选D.D3.(2019·河南省开封一中月考)下列各数中与1 010(4)相等的数是( )
(A)76(9) (B)103(8)
(C)1 000 100(2) (D)2 111(3)解析:1 010(4)=1×43+0×42+1×41+0×40=68(10),
1 000 100(2)=1×26+1×22=68(10).故选C.C4.用辗转相除法和更相减损术求1 515与600的最大公约数,需要运算的次数分别为( )
(A)4,15 (B)5,14 (C)5,13 (D)4,12解析:辗转相除法:1 515=600×2+315;600=315×1+285,315=285×1
+30,285=30×9+15,30=15×2,故最大公约数为15,且需计算5次.用更相减损术法:1 515-600=915,915-600=315,600-315=285,315-285=30,
285-30=255,255-30=225,225-30=195,195-30=165,165-30=135,135-30=105,105-30=75,75-30=45,45-30=15,30-15=15,故最大公约数为15,且需计算14次.故选B.B
