人教A版高中数学必修三 课件:第1章末总结 :31张PPT
文档属性
| 名称 | 人教A版高中数学必修三 课件:第1章末总结 :31张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 19:41:23 | ||
图片预览









文档简介
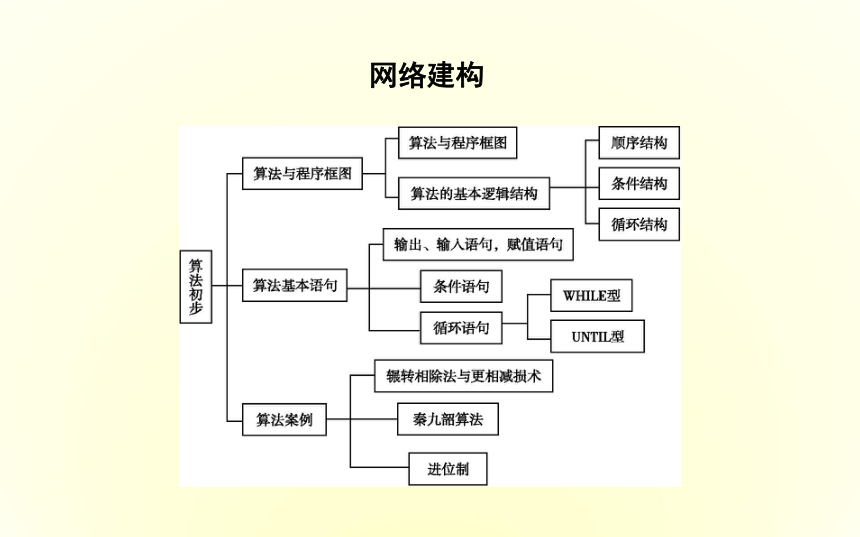
课件31张PPT。章末总结网络建构2.在程序框图中的判断框都有两个出口,按照条件成立与否确定不同的执行方向.( )
3.在算法语句中“=”是赋值符号,它把表达式右端的值赋予左端.( )
4.只有辗转相除法和更相减损术能够求两个正整数的最大值公约数.
( )
5.只有秦九韶算法能够计算多项式的值.( )
6.不同进位制之间的数不能直接比较大小.( )知识辨析判断下列说法是否正确(请在括号内填“√”或“×”)
1.任何程序都有终端框,它表示一个算法的结束.( )√√√××√题型归纳·素养提升题型一 算法的设计
[典例1] 已知一次函数图象过点A(1,1),B(2,4),写出求一次函数解析式的算法.解:算法分析:一次函数解析式是y=kx+b,设出这个解析式,图象上点的坐标适合这个解析式,代入后组成方程组求解k,b即可.规律方法一般地,设计算法有两个步骤,第一步进行算法分析,即分析这个问题是如何解决的,第二步写出算法,即把解决问题的方法,按照其各个步骤的先后顺序写出解决问题的步骤.题型二 程序框图的运行
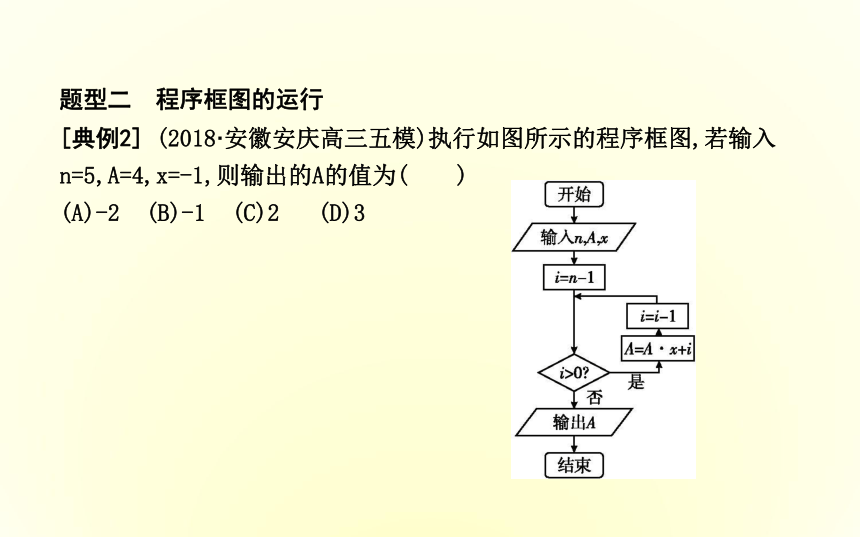
[典例2] (2018·安徽安庆高三五模)执行如图所示的程序框图,若输入n=5,A=4,x=-1,则输出的A的值为( )
(A)-2 (B)-1 (C)2 (D)3解析:输入n=5,A=4,x=-1,i=4;
第一次循环,A=0,i=3;
第二次循环,A=3,i=2;
第三次循环,A=-1,i=1;
第四次循环,A=2,i=0;
退出循环,输出A=2,故选C.规律方法只需根据框图给出的算法一步一步计算即可,要特别注意判断条件的应用.规律方法根据框图给出的算法和输出结果,结合选项填写判断条件,最好把选项中判断条件直接填入,运行程序,看输出结果是否与已知相符.题型四 算法基本语句
[典例4] (2019·福建永春一中月考)根据下列算法语句,当输入x为60时,输出y的值为( )INPUT x
IF x<=50 THEN
y=0.5*x
ELSE
y=25+0.6*(x-50)
END IF
PRINT y
END(A)25 (B)30 (C)31 (D)61解析:因为x=60>50,所以y=25+0.6×(60-50)=31,故选C.规律方法算法语句类似程序框图,只需根据由算法语句编写的算法,执行计算即可.题型五 算法案例
[典例5] (1)(2019·贵州铜仁一中期中)用秦九韶算法计算多项式f(x)=7x7+6x6+5x5+4x4+3x3+2x2+x在x=3时,求v4(v4表示由内到外第四个一次多项式的值)( )
(A)789 (B)-86 (C)262 (D)-262解析:
(1)f(x)=7x7+6x6+5x5+4x4+3x3+2x2+x=((((((7x+6)x+5)x+4)x+3)x+2)x
+1)x,
故v4=(((7x+6)x+5)x+4)x+3,
当x=3时,v4=(((7×3+6)×3+5)×3+4)×3+3=789.故选A.(2)(2019·哈师青冈实验中学期中)如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”.若输入的m,n分别为385,105,执行该程序框图(图中“m MOD n”表示m除以n的余数,例:11 MOD 7=4),则输出的m等于( )(A)0 (B)15 (C)35 (D)70解析:(2)模拟执行程序,可得m=385,n=105,
执行循环体,r=70,m=105,n=70,
不满足条件r=0,执行循环体,r=35,m=70,n=35,
不满足条件r=0,执行循环体,r=0,m=35,n=0,
满足条件r=0,退出循环,输出的m值为35,
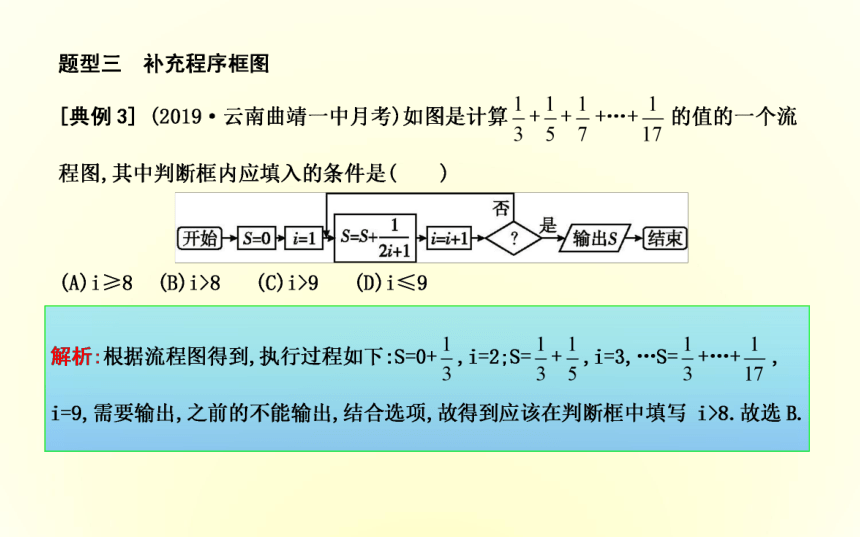
故选C.规律方法(1)注意进位制的转化;(2)注意改写多项式后,解决秦九韶算法中相关的问题,其中缺少的多项式系数用0补全;(3)辗转相除法和更相减损术是求两个正整数的最大公约数的算法,输出结果也可以通过直接计算两个正整数的最大公约数得出.真题体验·素养升级(A)i=i+1 (B)i=i+2
(C)i=i+3 (D)i=i+4B 解析:把各循环变量在各次循环中的值用表格表示如下.2.(2018·天津卷)阅读如图所示的程序框图,运行相应的程序,若输入N的值为20,则输出T的值为( )B(A)1 (B)2 (C)3 (D)43.(2017·全国Ⅱ卷)执行如图所示的程序框图,如果输入的a=-1,则输出的S等于( )(A)2 (B)3 (C)4 (D)5B解析:程序执行如下
a=-1,S=0,K=1?S=0+(-1)×1=-1,a=1,K=2.
?S=-1+1×2=1,a=-1,K=3,
?S=1+(-1)×3=-2,a=1,K=4,
?S=-2+1×4=2,a=-1,K=5,
?S=2+(-1)×5=-3,a=1,K=6,
?S=-3+1×6=3,a=-1,K=7>6,
?输出S=3.故选B.D (A)A>1 000和n=n+1 (B)A>1 000和n=n+2
(C)A≤1 000和n=n+1 (D)A≤1 000和n=n+2解析:由于本题是求满足3n-2n>1 000的最小偶数,
因此菱形框中应填A≤1 000,而矩形框中应填n=n+2.故选D.5.(2017·全国Ⅲ卷)执行如图的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )(A)5 (B)4 (C)3 (D)2D解析:执行程序:t=1,S=100,M=-10;
t=2,S=90,M=1,t=3;
知S=90<91时,t=3.
故N的最小值为2.
选D.6.(2017·北京卷)执行如图所示的程序框图,输出的s值为( )C
3.在算法语句中“=”是赋值符号,它把表达式右端的值赋予左端.( )
4.只有辗转相除法和更相减损术能够求两个正整数的最大值公约数.
( )
5.只有秦九韶算法能够计算多项式的值.( )
6.不同进位制之间的数不能直接比较大小.( )知识辨析判断下列说法是否正确(请在括号内填“√”或“×”)
1.任何程序都有终端框,它表示一个算法的结束.( )√√√××√题型归纳·素养提升题型一 算法的设计
[典例1] 已知一次函数图象过点A(1,1),B(2,4),写出求一次函数解析式的算法.解:算法分析:一次函数解析式是y=kx+b,设出这个解析式,图象上点的坐标适合这个解析式,代入后组成方程组求解k,b即可.规律方法一般地,设计算法有两个步骤,第一步进行算法分析,即分析这个问题是如何解决的,第二步写出算法,即把解决问题的方法,按照其各个步骤的先后顺序写出解决问题的步骤.题型二 程序框图的运行
[典例2] (2018·安徽安庆高三五模)执行如图所示的程序框图,若输入n=5,A=4,x=-1,则输出的A的值为( )
(A)-2 (B)-1 (C)2 (D)3解析:输入n=5,A=4,x=-1,i=4;
第一次循环,A=0,i=3;
第二次循环,A=3,i=2;
第三次循环,A=-1,i=1;
第四次循环,A=2,i=0;
退出循环,输出A=2,故选C.规律方法只需根据框图给出的算法一步一步计算即可,要特别注意判断条件的应用.规律方法根据框图给出的算法和输出结果,结合选项填写判断条件,最好把选项中判断条件直接填入,运行程序,看输出结果是否与已知相符.题型四 算法基本语句
[典例4] (2019·福建永春一中月考)根据下列算法语句,当输入x为60时,输出y的值为( )INPUT x
IF x<=50 THEN
y=0.5*x
ELSE
y=25+0.6*(x-50)
END IF
PRINT y
END(A)25 (B)30 (C)31 (D)61解析:因为x=60>50,所以y=25+0.6×(60-50)=31,故选C.规律方法算法语句类似程序框图,只需根据由算法语句编写的算法,执行计算即可.题型五 算法案例
[典例5] (1)(2019·贵州铜仁一中期中)用秦九韶算法计算多项式f(x)=7x7+6x6+5x5+4x4+3x3+2x2+x在x=3时,求v4(v4表示由内到外第四个一次多项式的值)( )
(A)789 (B)-86 (C)262 (D)-262解析:
(1)f(x)=7x7+6x6+5x5+4x4+3x3+2x2+x=((((((7x+6)x+5)x+4)x+3)x+2)x
+1)x,
故v4=(((7x+6)x+5)x+4)x+3,
当x=3时,v4=(((7×3+6)×3+5)×3+4)×3+3=789.故选A.(2)(2019·哈师青冈实验中学期中)如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”.若输入的m,n分别为385,105,执行该程序框图(图中“m MOD n”表示m除以n的余数,例:11 MOD 7=4),则输出的m等于( )(A)0 (B)15 (C)35 (D)70解析:(2)模拟执行程序,可得m=385,n=105,
执行循环体,r=70,m=105,n=70,
不满足条件r=0,执行循环体,r=35,m=70,n=35,
不满足条件r=0,执行循环体,r=0,m=35,n=0,
满足条件r=0,退出循环,输出的m值为35,
故选C.规律方法(1)注意进位制的转化;(2)注意改写多项式后,解决秦九韶算法中相关的问题,其中缺少的多项式系数用0补全;(3)辗转相除法和更相减损术是求两个正整数的最大公约数的算法,输出结果也可以通过直接计算两个正整数的最大公约数得出.真题体验·素养升级(A)i=i+1 (B)i=i+2
(C)i=i+3 (D)i=i+4B 解析:把各循环变量在各次循环中的值用表格表示如下.2.(2018·天津卷)阅读如图所示的程序框图,运行相应的程序,若输入N的值为20,则输出T的值为( )B(A)1 (B)2 (C)3 (D)43.(2017·全国Ⅱ卷)执行如图所示的程序框图,如果输入的a=-1,则输出的S等于( )(A)2 (B)3 (C)4 (D)5B解析:程序执行如下
a=-1,S=0,K=1?S=0+(-1)×1=-1,a=1,K=2.
?S=-1+1×2=1,a=-1,K=3,
?S=1+(-1)×3=-2,a=1,K=4,
?S=-2+1×4=2,a=-1,K=5,
?S=2+(-1)×5=-3,a=1,K=6,
?S=-3+1×6=3,a=-1,K=7>6,
?输出S=3.故选B.D (A)A>1 000和n=n+1 (B)A>1 000和n=n+2
(C)A≤1 000和n=n+1 (D)A≤1 000和n=n+2解析:由于本题是求满足3n-2n>1 000的最小偶数,
因此菱形框中应填A≤1 000,而矩形框中应填n=n+2.故选D.5.(2017·全国Ⅲ卷)执行如图的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )(A)5 (B)4 (C)3 (D)2D解析:执行程序:t=1,S=100,M=-10;
t=2,S=90,M=1,t=3;
知S=90<91时,t=3.
故N的最小值为2.
选D.6.(2017·北京卷)执行如图所示的程序框图,输出的s值为( )C
