人教A版高中数学必修三 课件:2.2.2 用样本的数字特征估计总体的数字特征 :44张PPT
文档属性
| 名称 | 人教A版高中数学必修三 课件:2.2.2 用样本的数字特征估计总体的数字特征 :44张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 19:51:37 | ||
图片预览











文档简介
课件44张PPT。2.2.2 用样本的数字特征估计总体的数字特征[目标导航]新知导学·素养养成1.众数、中位数、平均数最多底边中点集中趋势相等底边中点的横坐标 思考1:平均数、中位数、众数中,哪个量与样本的每一个数据有关,它有何缺点?
答案:平均数与样本的每一个数据有关,它可以反映出更多的关于样本数据总体的信息,但是平均数受数据中极端值的影响较大.2.标准差与方差的概念
(1)标准差
①定义:标准差是样本数据到平均数的一种 ,一般用s表示.
②计算公式:
s= .?
(2)方差
①定义:标准差的平方.
②计算公式:
s2= .平均距离思考2:当样本数据的标准差为0时,该组数据有何特点?
答案:当样本数据的标准差为0时,该组数据都相等.
思考3:标准差、方差的意义是什么?
答案:标准差、方差描述了一组数据围绕平均数波动的大小.标准差、方差越大,数据的离散程度越大;标准差、方差越小,数据的离散程度越小.名师点津(2)用样本的基本数字特征估计总体的基本数字特征的理解
①样本的基本数字特征包括众数、中位数、平均数、标准差.②平均数向我们提供了样本数据的重要信息,但是平均数有时也会使我们作出对总体的片面判断,因为这个平均数掩盖了一些极端的情况,而这些极端情况显然是不能忽视的.因此,还需要用标准差来反映数据的分散程度.
③现实中的总体所包含的个体数往往是很多的,虽然总体的平均数与标准差客观存在,但是我们无从知道.所以通常的做法是用样本的平均数和标准差去估计总体的平均数与标准差.虽然样本具有随机性,不同的样本测得的数据不一样,与总体的数字特征也可能不同,但只要样本的代表性好,这样做就是合理的,也是可以接受的.课堂探究·素养提升题型一 求众数、中位数、平均数
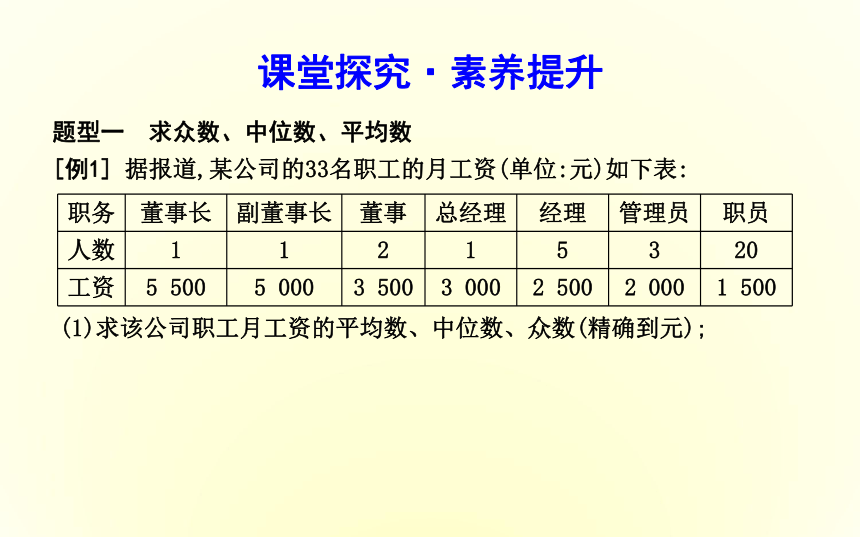
[例1] 据报道,某公司的33名职工的月工资(单位:元)如下表:(1)求该公司职工月工资的平均数、中位数、众数(精确到元);(2)假设副董事长的工资从5 000元提升到20 000元,董事长的工资从5 500元提升到30 000元,那么新的平均数、中位数、众数又是多少?(精确到元)
(3)你认为哪个统计量更能反映这个公司职工的工资水平?结合此问题谈一谈你的看法.(3)在这个问题中,中位数或众数均能反映该公司员工的工资水平.因为公司中少数人的工资额与大多数人的工资额差别较大,这样导致平均数与中位数偏差较大,所以平均数不能反映这个公司职工的工资水平.误区警示(1)众数、中位数及平均数都是描述一组数据集中趋势的量,平均数是最重要的量.由于平均数与每一个样本数据有关,因此,任何一个样本数据的改变都会引起平均数的改变.这是中位数、众数都不具有的性质.
(2)众数反映各数据出现的频率,其大小只与这组数据中的部分数据有关,当一组数据中有数据多次重复出现时,其众数往往更能反映问题.
(3)中位数仅与数据的排列位置有关,某些数据的变动对中位数没有影响,中位数可能出现在所给数据中,也可能不在所给数据中.当一组数据中仅有个别数据变动较大时,可用中位数描述其集中趋势.即时训练1-1:对于数据3,3,2,3,6,3,10,3,6,3,2,有以下结论:
①这组数据的众数是3;②这组数据的众数与中位数的数值不相等;③这组数据的中位数与平均数的数值相等;④这组数据的平均数与众数的数值相等.
其中正确的结论有( )
(A)1个 (B)2个 (C)3个 (D)4个题型二 方差、标准差的应用
[例2] (1)如图是Ⅰ,Ⅱ两组各7名同学体重(单位:kg)数据的茎叶图.设Ⅰ,Ⅱ两组数据的平均数依次为和,标准差依次为s1和s2,那么( )答案:(1)D (2)在某电视台举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图如图所示,去掉一个最高分和一个最低分后,所剩数据的方差是 .?方法技巧标准差(方差)的两个作用
(1)标准差(方差)较大,数据的离散程度较大;标准差(方差)较小,数据的离散程度较小.
(2)在实际应用中,常常把平均数与标准差结合起来进行决策.在平均值相等的情况下,比较方差或标准差以确定稳定性.即时训练2-1:已知母鸡产蛋的最佳温度在10 ℃左右,下面是在甲、乙两地六个时刻测得的温度,你认为甲、乙两地哪个地方更适合母鸡产蛋?②极差:甲地温度极差为15-(-5)=20;
乙地温度极差为10-0=10.[备用例2] 某市有210名初中生参加数学竞赛预赛,随机调阅了60名学生的答卷,成绩如表:(1)求样本的平均成绩和标准差(精确到0.01分);(2)若规定预赛成绩在7分或7分以上的学生参加复赛,试估计有多少名学生可以进入复赛.题型三 频率分布直方图中的样本数字特征
[例3] 从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:(1)作出这些数据的频率分布直方图;解:(1)(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定?(3)质量指标值不低于95的产品所占比例的估计值为0.38+0.22+0.08=0.68.
由于该估计值小于0.8,故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定.方法技巧(1)频率分布直方图中的众数是最高小长方形底边中点的横坐标,中位数是平分频率分布直方图面积且垂直于横轴的直线与横轴交点的横坐标,即累积频率为0.5的样本数据值.
(2)根据频率分布直方图求平均数的方法:频率分布直方图中每个小长方形的面积乘小长方形底边中点的横坐标之和.即时训练3-1:某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.(1)求这次测试数学成绩的众数;解:(1)由众数的概念可知,众数是出现次数最多的数,在直方图中,高度最高的小矩形的中间值的横坐标即为所求,所以成绩的众数是75.(2)求这次测试数学成绩的中位数;(3)求这次测试数学成绩的平均分.解:(3)平均数等于频率分布直方图中每个小矩形的面积乘小矩形底边中点的横坐标之和.
所以平均成绩为45×(0.005×10)+55×(0.015×10)+65×(0.020×10)+
75×(0.030×10)+85×(0.025×10)+95×(0.005×10)=72.
所以成绩的平均分为72分.[备用例1] 某学校1 800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个作为样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按分组方法得到的频率分布直方图.(1)若成绩小于15秒认为良好,求该样本在这次百米测试中成绩良好的人数;
(2)请估计学校1 800名学生中,成绩属于第四组的人数;解:(1)样本在这次百米测试中成绩良好的人数为0.22×50=11(人).(2)学校1 800名学生中,成绩属于第四组的人数为0.32×1 800=576(人).(3)请根据频率分布直方图,求样本数据的众数、中位数、平均数和方差.题型四 茎叶图中的样本数字特征
[例4] (2015·山东卷)为比较甲、乙两地某月14时的气温情况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的统计结论的编号为( )
(A)①③ (B)①④ (C)②③ (D)②④方法技巧通过茎叶图求解样本数据的众数、中位数、平均数、标准差及方差的过程与通过频率分布直方图求解不完全相同,但是各个数据所表示的数学含义完全相同.即时训练4-1:某市为了考核甲、乙两部门的工作情况,随机访问了50位市民.根据这50位市民对这两部门的评分(评分越高表明市民的评价越高),绘制茎叶图如下:(1)分别估计该市的市民对甲、乙两部门评分的中位数;
(2)分别估计该市的市民对甲、乙两部门的评分高于90的概率;(3)根据茎叶图分析该市的市民对甲、乙两部门的评价.解:(3)由所给茎叶图知,市民对甲部门的评分的中位数高于对乙部门的评分的中位数,而且由茎叶图可以大致看出对甲部门的评分的标准差要小于对乙部门的评分的标准差,说明该市市民对甲部门的评价较高、评价较为一致,对乙部门的评价较低、评价差异较大.[备用例2] 从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:
mm),结果如下:
甲品种:271,273,280,285,285,287,292,294,295,301,303,303,307,308,
310,314,319,323,325,325,328,331,334,337,352
乙品种:284,292,295,304,306,307,312,313,315,315,316,318,318,320,
322,322,324,327,329,331,333,336,337,343,356
由以上数据设计茎叶图,并根据茎叶图写出统计结论.解:茎叶图如图.
统计结论如下.
(1)乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度(或:乙品种棉花的纤维长度普遍大于甲品种棉花的纤维长度).
(2)甲品种棉花的纤维长度较乙品种棉花的纤维长度更分散(或:乙品种棉花的纤维长度较甲品种棉花的纤维长度更集中(稳定).甲品种棉花的纤维长度的分散程度更大).
(3)甲品种棉花的纤维长度的中位数是307 mm,乙品种棉花的纤维长度的中位数为318 mm.学霸经验分享区众数容易得出,但只能表达样本数据中的很少一部分信息,不一定唯一;中位数仅利用了数据中排在中间数据的信息,与数据的排列位置有关;平均数代表了数据更多的信息,描述了数据的平均水平,是一组数据的“重心”.课堂达标1.给出下列数据:3,9,8,3,4,3,5,则众数与极差分别是( )
(A)3,9 (B)3,6 (C)5,1 (D)9,9B解析:出现次数最多的是3,即众数是3.最大值9与最小值3的差为6,即极差是6.故选B.2.某校高一年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数和平均数分别是( )
(A)91.5和91.5 (B)91.5和92
(C)91和91.5 (D)92和92AA 4.某班十名同学的数学成绩:82,91,73,84,98,110,99,101,98,118,则该组数据的众数、中位数分别是( )
(A)98,98 (B)118,98 (C)74,85 (D)98,110A5.在如图所示的茎叶图中,甲、乙两组数据的中位数分别是 、
.?解析:甲位于中间的数是45,把乙的数据排序后,位于中间的数是46.答案:45 46
答案:平均数与样本的每一个数据有关,它可以反映出更多的关于样本数据总体的信息,但是平均数受数据中极端值的影响较大.2.标准差与方差的概念
(1)标准差
①定义:标准差是样本数据到平均数的一种 ,一般用s表示.
②计算公式:
s= .?
(2)方差
①定义:标准差的平方.
②计算公式:
s2= .平均距离思考2:当样本数据的标准差为0时,该组数据有何特点?
答案:当样本数据的标准差为0时,该组数据都相等.
思考3:标准差、方差的意义是什么?
答案:标准差、方差描述了一组数据围绕平均数波动的大小.标准差、方差越大,数据的离散程度越大;标准差、方差越小,数据的离散程度越小.名师点津(2)用样本的基本数字特征估计总体的基本数字特征的理解
①样本的基本数字特征包括众数、中位数、平均数、标准差.②平均数向我们提供了样本数据的重要信息,但是平均数有时也会使我们作出对总体的片面判断,因为这个平均数掩盖了一些极端的情况,而这些极端情况显然是不能忽视的.因此,还需要用标准差来反映数据的分散程度.
③现实中的总体所包含的个体数往往是很多的,虽然总体的平均数与标准差客观存在,但是我们无从知道.所以通常的做法是用样本的平均数和标准差去估计总体的平均数与标准差.虽然样本具有随机性,不同的样本测得的数据不一样,与总体的数字特征也可能不同,但只要样本的代表性好,这样做就是合理的,也是可以接受的.课堂探究·素养提升题型一 求众数、中位数、平均数
[例1] 据报道,某公司的33名职工的月工资(单位:元)如下表:(1)求该公司职工月工资的平均数、中位数、众数(精确到元);(2)假设副董事长的工资从5 000元提升到20 000元,董事长的工资从5 500元提升到30 000元,那么新的平均数、中位数、众数又是多少?(精确到元)
(3)你认为哪个统计量更能反映这个公司职工的工资水平?结合此问题谈一谈你的看法.(3)在这个问题中,中位数或众数均能反映该公司员工的工资水平.因为公司中少数人的工资额与大多数人的工资额差别较大,这样导致平均数与中位数偏差较大,所以平均数不能反映这个公司职工的工资水平.误区警示(1)众数、中位数及平均数都是描述一组数据集中趋势的量,平均数是最重要的量.由于平均数与每一个样本数据有关,因此,任何一个样本数据的改变都会引起平均数的改变.这是中位数、众数都不具有的性质.
(2)众数反映各数据出现的频率,其大小只与这组数据中的部分数据有关,当一组数据中有数据多次重复出现时,其众数往往更能反映问题.
(3)中位数仅与数据的排列位置有关,某些数据的变动对中位数没有影响,中位数可能出现在所给数据中,也可能不在所给数据中.当一组数据中仅有个别数据变动较大时,可用中位数描述其集中趋势.即时训练1-1:对于数据3,3,2,3,6,3,10,3,6,3,2,有以下结论:
①这组数据的众数是3;②这组数据的众数与中位数的数值不相等;③这组数据的中位数与平均数的数值相等;④这组数据的平均数与众数的数值相等.
其中正确的结论有( )
(A)1个 (B)2个 (C)3个 (D)4个题型二 方差、标准差的应用
[例2] (1)如图是Ⅰ,Ⅱ两组各7名同学体重(单位:kg)数据的茎叶图.设Ⅰ,Ⅱ两组数据的平均数依次为和,标准差依次为s1和s2,那么( )答案:(1)D (2)在某电视台举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图如图所示,去掉一个最高分和一个最低分后,所剩数据的方差是 .?方法技巧标准差(方差)的两个作用
(1)标准差(方差)较大,数据的离散程度较大;标准差(方差)较小,数据的离散程度较小.
(2)在实际应用中,常常把平均数与标准差结合起来进行决策.在平均值相等的情况下,比较方差或标准差以确定稳定性.即时训练2-1:已知母鸡产蛋的最佳温度在10 ℃左右,下面是在甲、乙两地六个时刻测得的温度,你认为甲、乙两地哪个地方更适合母鸡产蛋?②极差:甲地温度极差为15-(-5)=20;
乙地温度极差为10-0=10.[备用例2] 某市有210名初中生参加数学竞赛预赛,随机调阅了60名学生的答卷,成绩如表:(1)求样本的平均成绩和标准差(精确到0.01分);(2)若规定预赛成绩在7分或7分以上的学生参加复赛,试估计有多少名学生可以进入复赛.题型三 频率分布直方图中的样本数字特征
[例3] 从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:(1)作出这些数据的频率分布直方图;解:(1)(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定?(3)质量指标值不低于95的产品所占比例的估计值为0.38+0.22+0.08=0.68.
由于该估计值小于0.8,故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定.方法技巧(1)频率分布直方图中的众数是最高小长方形底边中点的横坐标,中位数是平分频率分布直方图面积且垂直于横轴的直线与横轴交点的横坐标,即累积频率为0.5的样本数据值.
(2)根据频率分布直方图求平均数的方法:频率分布直方图中每个小长方形的面积乘小长方形底边中点的横坐标之和.即时训练3-1:某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.(1)求这次测试数学成绩的众数;解:(1)由众数的概念可知,众数是出现次数最多的数,在直方图中,高度最高的小矩形的中间值的横坐标即为所求,所以成绩的众数是75.(2)求这次测试数学成绩的中位数;(3)求这次测试数学成绩的平均分.解:(3)平均数等于频率分布直方图中每个小矩形的面积乘小矩形底边中点的横坐标之和.
所以平均成绩为45×(0.005×10)+55×(0.015×10)+65×(0.020×10)+
75×(0.030×10)+85×(0.025×10)+95×(0.005×10)=72.
所以成绩的平均分为72分.[备用例1] 某学校1 800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个作为样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按分组方法得到的频率分布直方图.(1)若成绩小于15秒认为良好,求该样本在这次百米测试中成绩良好的人数;
(2)请估计学校1 800名学生中,成绩属于第四组的人数;解:(1)样本在这次百米测试中成绩良好的人数为0.22×50=11(人).(2)学校1 800名学生中,成绩属于第四组的人数为0.32×1 800=576(人).(3)请根据频率分布直方图,求样本数据的众数、中位数、平均数和方差.题型四 茎叶图中的样本数字特征
[例4] (2015·山东卷)为比较甲、乙两地某月14时的气温情况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的统计结论的编号为( )
(A)①③ (B)①④ (C)②③ (D)②④方法技巧通过茎叶图求解样本数据的众数、中位数、平均数、标准差及方差的过程与通过频率分布直方图求解不完全相同,但是各个数据所表示的数学含义完全相同.即时训练4-1:某市为了考核甲、乙两部门的工作情况,随机访问了50位市民.根据这50位市民对这两部门的评分(评分越高表明市民的评价越高),绘制茎叶图如下:(1)分别估计该市的市民对甲、乙两部门评分的中位数;
(2)分别估计该市的市民对甲、乙两部门的评分高于90的概率;(3)根据茎叶图分析该市的市民对甲、乙两部门的评价.解:(3)由所给茎叶图知,市民对甲部门的评分的中位数高于对乙部门的评分的中位数,而且由茎叶图可以大致看出对甲部门的评分的标准差要小于对乙部门的评分的标准差,说明该市市民对甲部门的评价较高、评价较为一致,对乙部门的评价较低、评价差异较大.[备用例2] 从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:
mm),结果如下:
甲品种:271,273,280,285,285,287,292,294,295,301,303,303,307,308,
310,314,319,323,325,325,328,331,334,337,352
乙品种:284,292,295,304,306,307,312,313,315,315,316,318,318,320,
322,322,324,327,329,331,333,336,337,343,356
由以上数据设计茎叶图,并根据茎叶图写出统计结论.解:茎叶图如图.
统计结论如下.
(1)乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度(或:乙品种棉花的纤维长度普遍大于甲品种棉花的纤维长度).
(2)甲品种棉花的纤维长度较乙品种棉花的纤维长度更分散(或:乙品种棉花的纤维长度较甲品种棉花的纤维长度更集中(稳定).甲品种棉花的纤维长度的分散程度更大).
(3)甲品种棉花的纤维长度的中位数是307 mm,乙品种棉花的纤维长度的中位数为318 mm.学霸经验分享区众数容易得出,但只能表达样本数据中的很少一部分信息,不一定唯一;中位数仅利用了数据中排在中间数据的信息,与数据的排列位置有关;平均数代表了数据更多的信息,描述了数据的平均水平,是一组数据的“重心”.课堂达标1.给出下列数据:3,9,8,3,4,3,5,则众数与极差分别是( )
(A)3,9 (B)3,6 (C)5,1 (D)9,9B解析:出现次数最多的是3,即众数是3.最大值9与最小值3的差为6,即极差是6.故选B.2.某校高一年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数和平均数分别是( )
(A)91.5和91.5 (B)91.5和92
(C)91和91.5 (D)92和92AA 4.某班十名同学的数学成绩:82,91,73,84,98,110,99,101,98,118,则该组数据的众数、中位数分别是( )
(A)98,98 (B)118,98 (C)74,85 (D)98,110A5.在如图所示的茎叶图中,甲、乙两组数据的中位数分别是 、
.?解析:甲位于中间的数是45,把乙的数据排序后,位于中间的数是46.答案:45 46
