人教A版高中数学必修四 课件:1.2.1 任意角的三角函数 :34张PPT
文档属性
| 名称 | 人教A版高中数学必修四 课件:1.2.1 任意角的三角函数 :34张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 20:14:22 | ||
图片预览











文档简介
课件34张PPT。1.2 任意角的三角函数
1.2.1 任意角的三角函数目标导航新知导学课堂探究新知导学·素养养成1.三角函数的定义
(1)单位圆中三角函数的定义:
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
①y叫做α的 ,记作 ,即sin α=y;?
②x叫做α的 ,记作 ,即cos α=x;?正弦sin α余弦 cos α正切tan α(2)任意角的三角函数的定义:
一般地,设角α终边上任意一点的坐标为(x,y),它与原点的距离为r,则sin α= ,cos α= ,tan α= (x≠0).2.正弦、余弦、正切函数值在各象限的符号思考:若sin θ>0,tan θ<0,则θ是第几象限角?
提示:由sin θ>0,tan θ<0,知θ是第二象限角.
3.终边相同的角的同一三角函数的值
(1)结论:终边相同的角的同一三角函数的值 .
(2)公式一:sin (α+k·2π)= .?
cos (α+k·2π)= .?
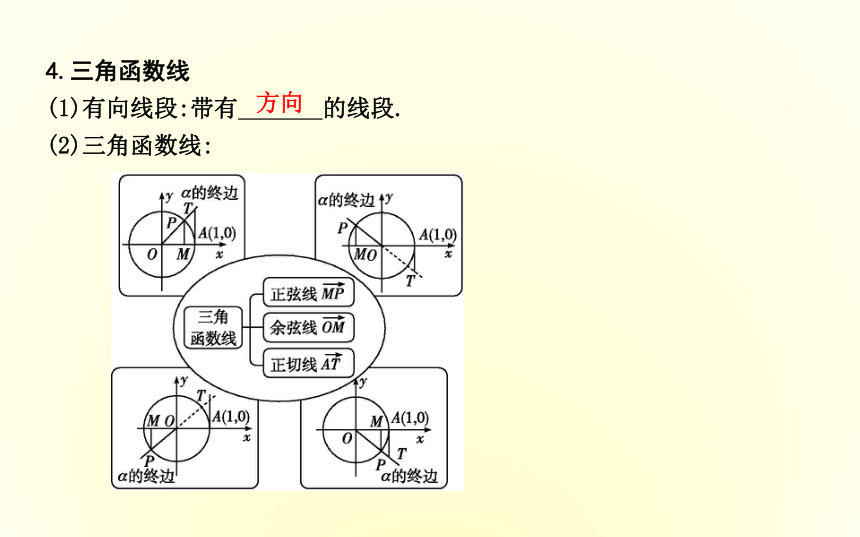
tan (α+k·2π)= .其中k∈Z.?相等sin α cos α tan α 4.三角函数线
(1)有向线段:带有 的线段.方向(2)三角函数线:课堂探究·素养提升题型一 用三角函数的定义求三角函数值
[例1] 已知角α的终边经过点P(-4a,3a)(a≠0),求sin α,cos α,tanα的值.互动探究:(教师备用)将本例中点P的坐标改为(-3a,4a)(a≠0),求2sinα+
cos α的值.方法技巧(1)求一个角的三角函数值,需确定三个量:角的终边上异于原点的点的横、纵坐标及其到原点的距离.当已知坐标含参数时需注意分类讨论;
(2)若终边在直线上时,因为角的终边是射线,应分两种情况处理;
(3)已知角求值时,可依据定义先确定出角的终边与单位圆的交点坐标再求值.[备用例1] 已知θ的终边经过点P(a,a)(a≠0),求sin θ,cos θ,tan θ的值.题型二 三角函数的符号问题
[例2] 判断下列各式的符号:
(1)α是第二象限角,sin α·cos α;
(2)sin 3·cos 4·tan (- ).解:(1)因为α是第二象限角,
所以sin α>0,cos α<0,所以sin α·cos α<0.方法技巧确定三角函数值在各象限内符号的方法
(1)三角函数值的符号是根据三角函数的定义,由各象限内的点的坐标的符号得出的;
(2)对正弦、余弦、正切函数的符号可用下列口诀记忆:“一全正,二正弦,三正切,四余弦”,该口诀表示:第一象限全是正值,第二象限正弦值是正值,第三象限正切值是正值,第四象限余弦值是正值.即时训练2-1:(2018·丹东市期末)若sin α>0且tan α<0,则 的终边在( )
(A)第一象限
(B)第二象限
(C)第一象限或第三象限
(D)第三象限或第四象限[备用例2] (1)α是第四象限角,则下列数值中一定是正值的是( )
(A)sin α (B)cos α
(C)tan α (D)cos α或tan α
(2)若sin θ·tan θ>0,cos θ·tan θ<0,则sin θ·cos θ 0
(填“>”“<”或“=”).?解析:(1)α是第四象限角,则cos α为正.故选B.
(2)由sin θ·tan θ>0,知sin θ与tan θ同号,θ是第一或第四象限角.又cos θ·tan θ<0,得θ是第三或第四象限角.
所以θ只能是第四象限角.
所以sin θ<0,cos θ>0.所以sin θ·cos θ<0.答案:(1)B (2)<题型三 诱导公式一的运用
[例3] 求下列各式的值:
(1)a2sin (-1 350°)+b2tan 405°-2abcos (-1 080°);解:(1)原式=a2sin (-4×360°+90°)+b2tan (360°+45°)-2abcos (-3×360°)
=a2sin 90°+b2tan 45°-2abcos 0°
=a2+b2-2ab=(a-b)2.方法技巧(1)诱导公式一可以统一写成f(k·360°+α)=f(α)或f(k·2π+α)=
f(α)(k∈Z)的形式,它的实质是终边相同的角的同一三角函数值相等;
(2)利用它可把任意角的三角函数值转化为0~2π角的三角函数值,即可把负角的三角函数化为0到2π间的三角函数,亦可把大于2π的角的三角函数化为0到2π间的三角函数,即把角实现大化小,负化正的转化.即时训练3-1:求下列各三角函数的值.[备用例3] 求值:(1)tan 405°-sin 450°+cos 750°;题型四 三角函数线及其应用
[例4] 在单位圆中画出适合下列条件的角α的终边范围,并由此写出角α的集合.(1)sin α≥ ; (2)cos α≤- .方法技巧(1)三角函数线是利用数形结合思想解决有关问题的工具,要注意利用其来解决问题;
(2)三角函数线的主要作用是解三角不等式、比较大小及求函数的定义域,在求三角函数定义域时,一般转化为不等式(组),因此必须牢固掌握三角函数线的画法及意义.题型五 易错辨析
[例5] 已知角α的终边过点P(-3m,m)(m≠0),则sin α= .?纠错:本例应按照m>0和m<0两种情况讨论.课堂达标C D 3.已知角α的终边在直线y=2x上,则sin α+2cos α的值为 .?4.若sin θ≥0,则θ的取值范围是 .? 解析:sin θ≥0,如图利用三角函数线可得2kπ≤θ≤2kπ+π,k∈Z.答案:[2kπ,2kπ+π](k∈Z)点击进入 课时作业
1.2.1 任意角的三角函数目标导航新知导学课堂探究新知导学·素养养成1.三角函数的定义
(1)单位圆中三角函数的定义:
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
①y叫做α的 ,记作 ,即sin α=y;?
②x叫做α的 ,记作 ,即cos α=x;?正弦sin α余弦 cos α正切tan α(2)任意角的三角函数的定义:
一般地,设角α终边上任意一点的坐标为(x,y),它与原点的距离为r,则sin α= ,cos α= ,tan α= (x≠0).2.正弦、余弦、正切函数值在各象限的符号思考:若sin θ>0,tan θ<0,则θ是第几象限角?
提示:由sin θ>0,tan θ<0,知θ是第二象限角.
3.终边相同的角的同一三角函数的值
(1)结论:终边相同的角的同一三角函数的值 .
(2)公式一:sin (α+k·2π)= .?
cos (α+k·2π)= .?
tan (α+k·2π)= .其中k∈Z.?相等sin α cos α tan α 4.三角函数线
(1)有向线段:带有 的线段.方向(2)三角函数线:课堂探究·素养提升题型一 用三角函数的定义求三角函数值
[例1] 已知角α的终边经过点P(-4a,3a)(a≠0),求sin α,cos α,tanα的值.互动探究:(教师备用)将本例中点P的坐标改为(-3a,4a)(a≠0),求2sinα+
cos α的值.方法技巧(1)求一个角的三角函数值,需确定三个量:角的终边上异于原点的点的横、纵坐标及其到原点的距离.当已知坐标含参数时需注意分类讨论;
(2)若终边在直线上时,因为角的终边是射线,应分两种情况处理;
(3)已知角求值时,可依据定义先确定出角的终边与单位圆的交点坐标再求值.[备用例1] 已知θ的终边经过点P(a,a)(a≠0),求sin θ,cos θ,tan θ的值.题型二 三角函数的符号问题
[例2] 判断下列各式的符号:
(1)α是第二象限角,sin α·cos α;
(2)sin 3·cos 4·tan (- ).解:(1)因为α是第二象限角,
所以sin α>0,cos α<0,所以sin α·cos α<0.方法技巧确定三角函数值在各象限内符号的方法
(1)三角函数值的符号是根据三角函数的定义,由各象限内的点的坐标的符号得出的;
(2)对正弦、余弦、正切函数的符号可用下列口诀记忆:“一全正,二正弦,三正切,四余弦”,该口诀表示:第一象限全是正值,第二象限正弦值是正值,第三象限正切值是正值,第四象限余弦值是正值.即时训练2-1:(2018·丹东市期末)若sin α>0且tan α<0,则 的终边在( )
(A)第一象限
(B)第二象限
(C)第一象限或第三象限
(D)第三象限或第四象限[备用例2] (1)α是第四象限角,则下列数值中一定是正值的是( )
(A)sin α (B)cos α
(C)tan α (D)cos α或tan α
(2)若sin θ·tan θ>0,cos θ·tan θ<0,则sin θ·cos θ 0
(填“>”“<”或“=”).?解析:(1)α是第四象限角,则cos α为正.故选B.
(2)由sin θ·tan θ>0,知sin θ与tan θ同号,θ是第一或第四象限角.又cos θ·tan θ<0,得θ是第三或第四象限角.
所以θ只能是第四象限角.
所以sin θ<0,cos θ>0.所以sin θ·cos θ<0.答案:(1)B (2)<题型三 诱导公式一的运用
[例3] 求下列各式的值:
(1)a2sin (-1 350°)+b2tan 405°-2abcos (-1 080°);解:(1)原式=a2sin (-4×360°+90°)+b2tan (360°+45°)-2abcos (-3×360°)
=a2sin 90°+b2tan 45°-2abcos 0°
=a2+b2-2ab=(a-b)2.方法技巧(1)诱导公式一可以统一写成f(k·360°+α)=f(α)或f(k·2π+α)=
f(α)(k∈Z)的形式,它的实质是终边相同的角的同一三角函数值相等;
(2)利用它可把任意角的三角函数值转化为0~2π角的三角函数值,即可把负角的三角函数化为0到2π间的三角函数,亦可把大于2π的角的三角函数化为0到2π间的三角函数,即把角实现大化小,负化正的转化.即时训练3-1:求下列各三角函数的值.[备用例3] 求值:(1)tan 405°-sin 450°+cos 750°;题型四 三角函数线及其应用
[例4] 在单位圆中画出适合下列条件的角α的终边范围,并由此写出角α的集合.(1)sin α≥ ; (2)cos α≤- .方法技巧(1)三角函数线是利用数形结合思想解决有关问题的工具,要注意利用其来解决问题;
(2)三角函数线的主要作用是解三角不等式、比较大小及求函数的定义域,在求三角函数定义域时,一般转化为不等式(组),因此必须牢固掌握三角函数线的画法及意义.题型五 易错辨析
[例5] 已知角α的终边过点P(-3m,m)(m≠0),则sin α= .?纠错:本例应按照m>0和m<0两种情况讨论.课堂达标C D 3.已知角α的终边在直线y=2x上,则sin α+2cos α的值为 .?4.若sin θ≥0,则θ的取值范围是 .? 解析:sin θ≥0,如图利用三角函数线可得2kπ≤θ≤2kπ+π,k∈Z.答案:[2kπ,2kπ+π](k∈Z)点击进入 课时作业
