人教A版高中数学必修四 课件:1.2.2 同角三角函数的基本关系 :30张PPT
文档属性
| 名称 | 人教A版高中数学必修四 课件:1.2.2 同角三角函数的基本关系 :30张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 20:16:56 | ||
图片预览










文档简介
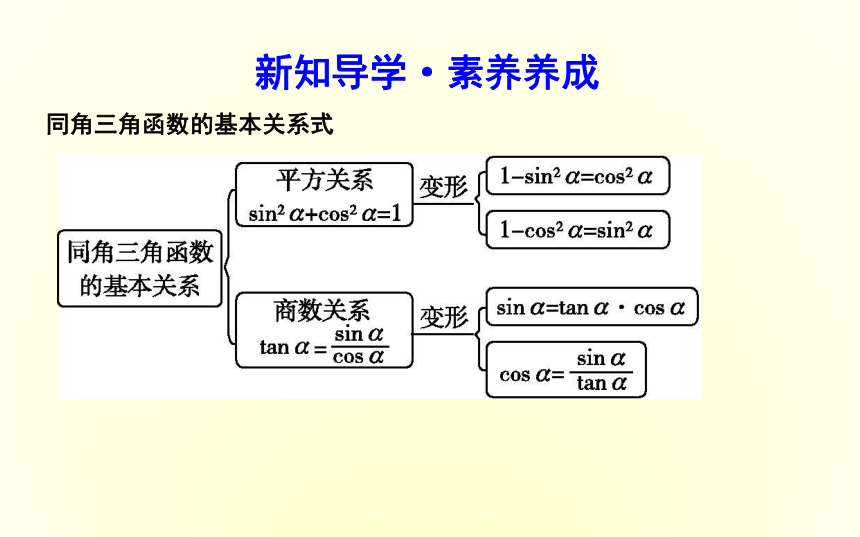
课件30张PPT。1.2.2 同角三角函数的基本关系目标导航新知导学课堂探究新知导学·素养养成同角三角函数的基本关系式思考:同角三角函数的基本关系式对任意角α都成立吗?课堂探究·素养提升题型一 利用同角三角函数关系求值(2)已知sin α=m(|m|<1),求tan α,cos α.方法技巧由某角的一个三角函数值求它的其余各三角函数值的依据及种类(2)分类:
①如果已知三角函数的值,且角的象限已被指定时,则只有一组解;
②如果已知三角函数的值,但没有指定角在哪个象限,那么由已知三角函数值确定角可能在的象限,然后再求解,这种情况一般有两组解;
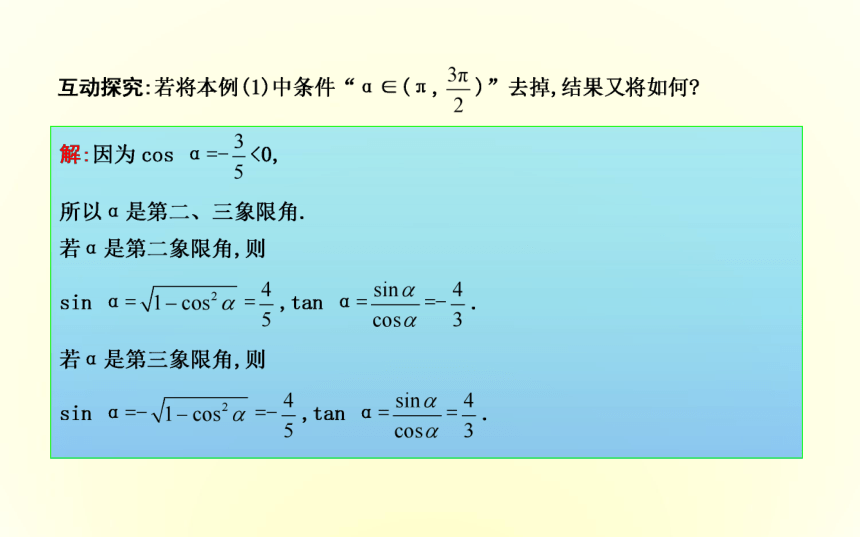
③如果所给的三角函数值含字母,且没有指定角在哪个象限,那么就需要进行讨论.即时训练1-1:已知α是第三象限角且tan α=2,求下列各式的值.
(1)cos α,sin α;(2) ;题型二 利用同角关系式化简三角函数式
[例2] (1)化简:sin2α+sin2β-sin2αsin2β+cos2αcos2β= ;?(1)解析:原式=sin2α(1-sin2β)+sin2β+cos2αcos2β
=sin2αcos2β+cos2αcos2β+sin2β
=(sin2α+cos2α)cos2β+sin2β=1.答案:1方法技巧(1)化简的标准:第一,尽量使函数种类最少,次数最低,而且尽量化成积的形式;第二,能求出值的要求出值;第三,根号内的三角函数式尽量开出;第四,尽量使分母不含三角函数;
(2)化简策略:在化简三角函数时,应注意“1”的代换,如sin2α+
cos2α=1.对于函数种类较多的式子,化简时,常用“切化弦法”.题型三 利用sin α±cos α与sin αcos α的关系解题
[例3] 已知0<α<π,sin α+cos α= ,求tan α的值.方法技巧(1)sin α+cos α,sin αcos α,sin α-cos α三个式子中,已知其中一个,可以求其他两个,即“知一求二”.它们的关系是:(sin α+
cos α)2=1+2sin αcos α;(sin α-cos α)2=1-2sin αcos α.
(2)求sin α+cos α或sin α-cos α的值,要注意判断它们的符号.即时训练3-1:已知sin θ,cos θ是关于x的方程x2-ax+a=0的两个根(a∈R).
求sin3θ+cos3θ的值.课堂达标B C 答案:二或四4.已知tan α= ,且α是第三象限角,求sin α,cos α的值.点击进入 课时作业点击进入 周练卷
①如果已知三角函数的值,且角的象限已被指定时,则只有一组解;
②如果已知三角函数的值,但没有指定角在哪个象限,那么由已知三角函数值确定角可能在的象限,然后再求解,这种情况一般有两组解;
③如果所给的三角函数值含字母,且没有指定角在哪个象限,那么就需要进行讨论.即时训练1-1:已知α是第三象限角且tan α=2,求下列各式的值.
(1)cos α,sin α;(2) ;题型二 利用同角关系式化简三角函数式
[例2] (1)化简:sin2α+sin2β-sin2αsin2β+cos2αcos2β= ;?(1)解析:原式=sin2α(1-sin2β)+sin2β+cos2αcos2β
=sin2αcos2β+cos2αcos2β+sin2β
=(sin2α+cos2α)cos2β+sin2β=1.答案:1方法技巧(1)化简的标准:第一,尽量使函数种类最少,次数最低,而且尽量化成积的形式;第二,能求出值的要求出值;第三,根号内的三角函数式尽量开出;第四,尽量使分母不含三角函数;
(2)化简策略:在化简三角函数时,应注意“1”的代换,如sin2α+
cos2α=1.对于函数种类较多的式子,化简时,常用“切化弦法”.题型三 利用sin α±cos α与sin αcos α的关系解题
[例3] 已知0<α<π,sin α+cos α= ,求tan α的值.方法技巧(1)sin α+cos α,sin αcos α,sin α-cos α三个式子中,已知其中一个,可以求其他两个,即“知一求二”.它们的关系是:(sin α+
cos α)2=1+2sin αcos α;(sin α-cos α)2=1-2sin αcos α.
(2)求sin α+cos α或sin α-cos α的值,要注意判断它们的符号.即时训练3-1:已知sin θ,cos θ是关于x的方程x2-ax+a=0的两个根(a∈R).
求sin3θ+cos3θ的值.课堂达标B C 答案:二或四4.已知tan α= ,且α是第三象限角,求sin α,cos α的值.点击进入 课时作业点击进入 周练卷
