人教A版高中数学必修四 课件:1.3 第二课时 三角函数的诱导公式五、六 :27张PPT
文档属性
| 名称 | 人教A版高中数学必修四 课件:1.3 第二课时 三角函数的诱导公式五、六 :27张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 20:27:08 | ||
图片预览








文档简介
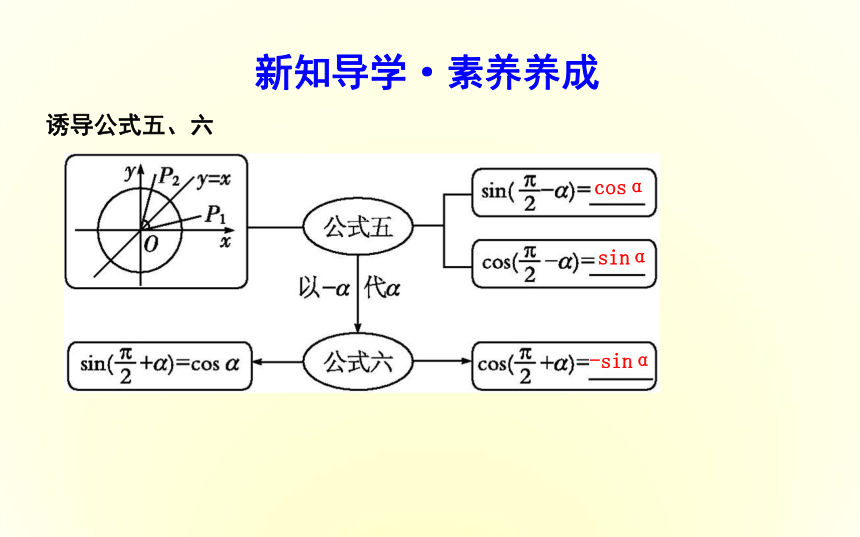
课件27张PPT。第二课时 三角函数的诱导公式五、六目标导航新知导学课堂探究新知导学·素养养成诱导公式五、六cosα sinα -sinα 公式五、六可以概括如下: ±α的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值,前面加上一个把α看成锐角时原函数值的符号,可以简单地说成“函数名改变,符号看象限”.1.利用诱导公式可得到如下结论名师点津课堂探究·素养提升题型一 利用诱导公式解决给角(或值)求值方法技巧角的转化方法
(1)对于负角的三角函数求值,可先利用诱导公式三,化为正角的三角函数.若转化了以后的正角大于360°,再利用诱导公式一,化为0°到360°间的角的三角函数.
(2)当化成的角是90°到180°间的角时,再利用180°-α的诱导公式化为0°到90°间的角的三角函数.
(3)当化成的角是270°到360°间的角,则利用360°-α及-α的诱导公式化为0°到90°间的角的三角函数.题型二 利用诱导公式化简求值(1)化简f(α);方法技巧用诱导公式化简求值的方法
(1)对于三角函数式的化简求值问题,一般遵循诱导公式先行的原则,即先用诱导公式化简变形,达到角的统一,再进行三角函数名称转化,以保证三角函数名称最少.
(2)对于kπ±α和 ±α这两套诱导公式,切记运用前一套公式不变名,而后一套公式必须变名.题型三 利用诱导公式进行证明方法技巧证明等式的常用方法
利用诱导公式证明等式问题,关键在于公式的灵活应用,其证明的常用方法有:
(1)从一边开始,使得它等于另一边,一般由繁到简.
(2)左右归一法:即证明左、右两边都等于同一个式子.
(3)针对题设与结论间的差异,有针对性地进行变形,以消除其差异,简言之,即化异为同.题型四 易错辨析纠错:将诱导公式五与诱导公式六混淆,弄错三角函数值的符号致误.课堂达标B1.sin 480°的值是( )A B (A)第一象限 (B)第二象限
(C)第三象限 (D)第四象限答案:sin2α点击进入 课时作业点击进入 周练卷
(1)对于负角的三角函数求值,可先利用诱导公式三,化为正角的三角函数.若转化了以后的正角大于360°,再利用诱导公式一,化为0°到360°间的角的三角函数.
(2)当化成的角是90°到180°间的角时,再利用180°-α的诱导公式化为0°到90°间的角的三角函数.
(3)当化成的角是270°到360°间的角,则利用360°-α及-α的诱导公式化为0°到90°间的角的三角函数.题型二 利用诱导公式化简求值(1)化简f(α);方法技巧用诱导公式化简求值的方法
(1)对于三角函数式的化简求值问题,一般遵循诱导公式先行的原则,即先用诱导公式化简变形,达到角的统一,再进行三角函数名称转化,以保证三角函数名称最少.
(2)对于kπ±α和 ±α这两套诱导公式,切记运用前一套公式不变名,而后一套公式必须变名.题型三 利用诱导公式进行证明方法技巧证明等式的常用方法
利用诱导公式证明等式问题,关键在于公式的灵活应用,其证明的常用方法有:
(1)从一边开始,使得它等于另一边,一般由繁到简.
(2)左右归一法:即证明左、右两边都等于同一个式子.
(3)针对题设与结论间的差异,有针对性地进行变形,以消除其差异,简言之,即化异为同.题型四 易错辨析纠错:将诱导公式五与诱导公式六混淆,弄错三角函数值的符号致误.课堂达标B1.sin 480°的值是( )A B (A)第一象限 (B)第二象限
(C)第三象限 (D)第四象限答案:sin2α点击进入 课时作业点击进入 周练卷
