人教A版高中数学必修四 课件:第1章末总结 (29张PPT)
文档属性
| 名称 | 人教A版高中数学必修四 课件:第1章末总结 (29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 20:29:51 | ||
图片预览








文档简介
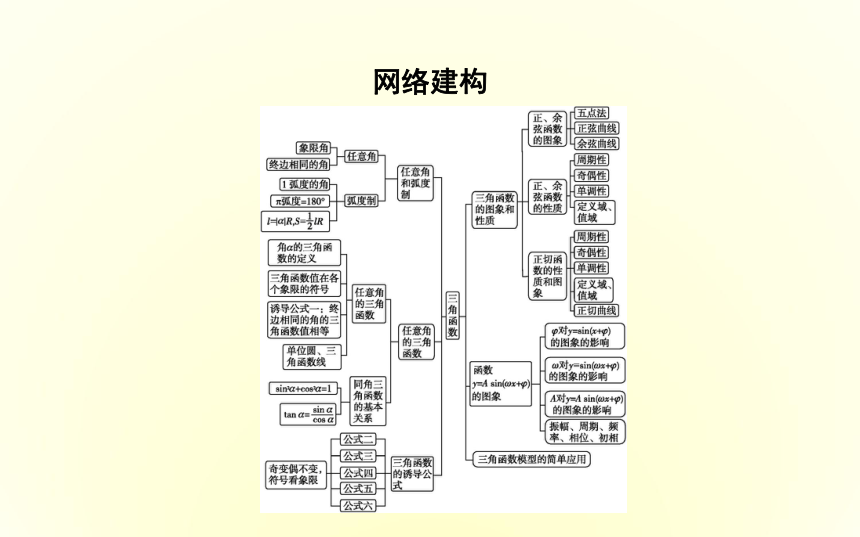
课件29张PPT。章末总结网络建构知识辨析判断下列说法是否正确,正确的在它后面的括号里打“√”,错误的打“×”.
1.锐角是第一象限角,反之亦然.( )×2.不相等的角终边一定不相同.( )
3.点P(tan α,cos α)在第三象限,则角α终边在第二象限.( )
4.若α,β为锐角,则sin2α+cos2β=1.( )×√× × × 7.正切函数y=tan x在定义域内是增函数.( )×× 9.已知y=ksin x+1,x∈R,则y的最大值为k+1.( )
10.y=sin |x|是偶函数.( )×√题型归纳真题赏析题型归纳·素养提升题型一 任意角的三角函数的定义及应用规律方法(1)利用三角函数的定义,已知角α终边上一点P的坐标可求α的三角函数值;已知角α的三角函数值,也可以求出点P的坐标或其他参数的取值.(2)利用三角函数的定义求三角函数值时,除了r是正值外,点的横、纵坐标都可正可负.要注意对符号的分类讨论.规律方法同角三角函数的基本关系和诱导公式是三角恒等变形的主要依据,主要应用方向是三角函数式的化简、求值和证明.常用以下方法技巧:
(1)化弦:当三角函数式中三角函数名称较多时,往往把三角函数化为弦,再化简变形.
(2)化切:当三角函数式中含有正切及其他三角函数时,有时可将三角函数名称都化为正切,再化简变形.
(3)“1”的代换:在三角函数式中,有些会含有常数1,常数1虽然非常简单,但有些三角函数式的化简却需要利用三角函数公式将1代换为三角函数式.题型三 三角函数的图象及变换
[典例3] (1)求此函数解析式;(2)分析一下该函数是如何通过y=sin x变换得来的?规律方法(1)求f(x)的单调区间;(3)求f(x)取最大值时x的取值集合.规律方法题型五 易错辨析
[典例5]函数y=cos2x-4cosx+5的值域是 .?错解:由于函数y=(cos x-2)2+1≥1,所以该函数的值域是[1,+∞).纠错:求函数值域时,树立定义域优先的原则.定义域是函数的三要素之一,研究函数的性质一般要先考虑函数的定义域,三角函数也不例外,当求其值域时,不要想当然认为定义域为R,另外在利用换元法求解有关“二次函数型”函数值域问题时要特别注意换元后“新元”的范围,以免扩大或缩小自变量的取值范围.本例在探求y=(cos x-2)2+1的值域时,误认为cos x∈R,而忽略了余弦函数的有界性,即|cos x|≤1.正解:令t=cos x,由于x∈R,故-1≤t≤1,
y=t2-4t+5=(t-2)2+1.
当t=-1,即cos x=-1时函数有最大值10;
当t=1,即cos x=1时函数有最小值2.
所以该函数的值域是[2,10].
答案:[2,10]真题赏析·素养升级C A A D 答案:3点击进入 检测试题
1.锐角是第一象限角,反之亦然.( )×2.不相等的角终边一定不相同.( )
3.点P(tan α,cos α)在第三象限,则角α终边在第二象限.( )
4.若α,β为锐角,则sin2α+cos2β=1.( )×√× × × 7.正切函数y=tan x在定义域内是增函数.( )×× 9.已知y=ksin x+1,x∈R,则y的最大值为k+1.( )
10.y=sin |x|是偶函数.( )×√题型归纳真题赏析题型归纳·素养提升题型一 任意角的三角函数的定义及应用规律方法(1)利用三角函数的定义,已知角α终边上一点P的坐标可求α的三角函数值;已知角α的三角函数值,也可以求出点P的坐标或其他参数的取值.(2)利用三角函数的定义求三角函数值时,除了r是正值外,点的横、纵坐标都可正可负.要注意对符号的分类讨论.规律方法同角三角函数的基本关系和诱导公式是三角恒等变形的主要依据,主要应用方向是三角函数式的化简、求值和证明.常用以下方法技巧:
(1)化弦:当三角函数式中三角函数名称较多时,往往把三角函数化为弦,再化简变形.
(2)化切:当三角函数式中含有正切及其他三角函数时,有时可将三角函数名称都化为正切,再化简变形.
(3)“1”的代换:在三角函数式中,有些会含有常数1,常数1虽然非常简单,但有些三角函数式的化简却需要利用三角函数公式将1代换为三角函数式.题型三 三角函数的图象及变换
[典例3] (1)求此函数解析式;(2)分析一下该函数是如何通过y=sin x变换得来的?规律方法(1)求f(x)的单调区间;(3)求f(x)取最大值时x的取值集合.规律方法题型五 易错辨析
[典例5]函数y=cos2x-4cosx+5的值域是 .?错解:由于函数y=(cos x-2)2+1≥1,所以该函数的值域是[1,+∞).纠错:求函数值域时,树立定义域优先的原则.定义域是函数的三要素之一,研究函数的性质一般要先考虑函数的定义域,三角函数也不例外,当求其值域时,不要想当然认为定义域为R,另外在利用换元法求解有关“二次函数型”函数值域问题时要特别注意换元后“新元”的范围,以免扩大或缩小自变量的取值范围.本例在探求y=(cos x-2)2+1的值域时,误认为cos x∈R,而忽略了余弦函数的有界性,即|cos x|≤1.正解:令t=cos x,由于x∈R,故-1≤t≤1,
y=t2-4t+5=(t-2)2+1.
当t=-1,即cos x=-1时函数有最大值10;
当t=1,即cos x=1时函数有最小值2.
所以该函数的值域是[2,10].
答案:[2,10]真题赏析·素养升级C A A D 答案:3点击进入 检测试题
