人教A版高中数学必修四 课件:2.2.1 向量加法运算及其几何意义 (39张PPT)
文档属性
| 名称 | 人教A版高中数学必修四 课件:2.2.1 向量加法运算及其几何意义 (39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 20:34:36 | ||
图片预览









文档简介
课件39张PPT。2.2 平面向量的线性运算
2.2.1 向量加法运算及其几何意义目标导航新知导学课堂探究1.向量加法的定义
定义:求两个向量 的运算,叫做向量的加法.
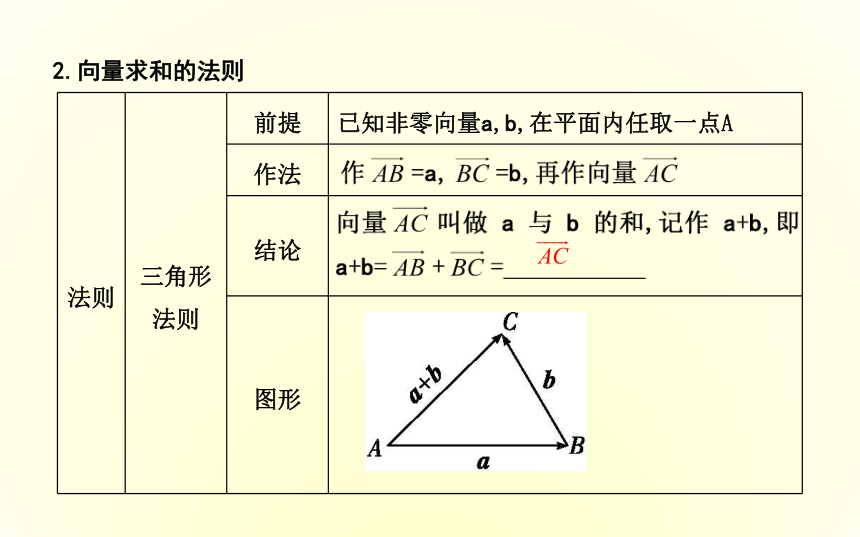
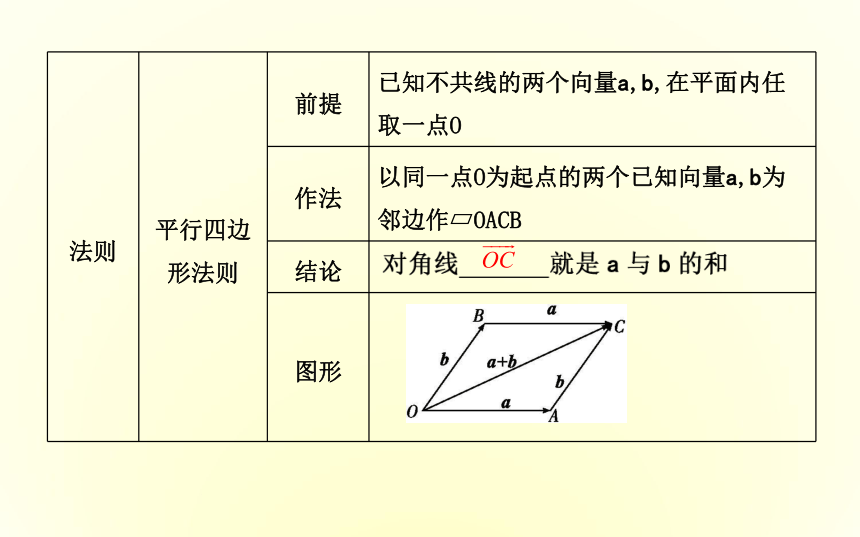
对于零向量与任一向量a,规定0+a=a+ = .0新知导学·素养养成a和2.向量求和的法则思考1:向量加法的三角形法则和平行四边形法则的使用条件有什么不同?
提示:三角形法则适用于任意两个非零向量求和,平行四边形法则只适用于两个不共线的向量求和.3.向量加法的运算律
(1)交换律:a+b= .
(2)结合律:(a+b)+c= .
4.重要结论
|a+b| |a|+|b|.b+aa+(b+c)≤思考2:(a+b)+(c+d)=(a+d)+(b+c)成立吗?
提示:成立.向量加法满足交换律和结合律,因此在进行多个向量的加法运算时,就可以按照任意的次序和任意的组合进行.名师点津(1)在使用向量加法的三角形法则时,应注意“首尾连接”;在使用平行四边形法则时,应注意范围的限制及和向量与两向量起点相同.
(2)向量a+b与非零向量a,b的模及方向的联系
①当两个非零向量a与b不共线时,由向量加法的三角形法则可知a+b的方向与a,b的方向都不相同,且 ||a|-|b||<|a+b|<|a|+|b|,几何意义是三角形两边之和大于第三边,两边之差小于第三边.
②当两个非零向量a与b共线且同向时(如图1),则向量a+b与a(或b)方向相同,且|a+b|=|a|+|b|.③当两个非零向量a与b反向且|a|<|b|时(如图2),则a+b与b方向相同(与a方向相反),且|a+b|=||a|-|b||.
④当两个向量a与b中至少有一个为0时,则必有|a+b|=|a|+|b|=||a|-|b||.
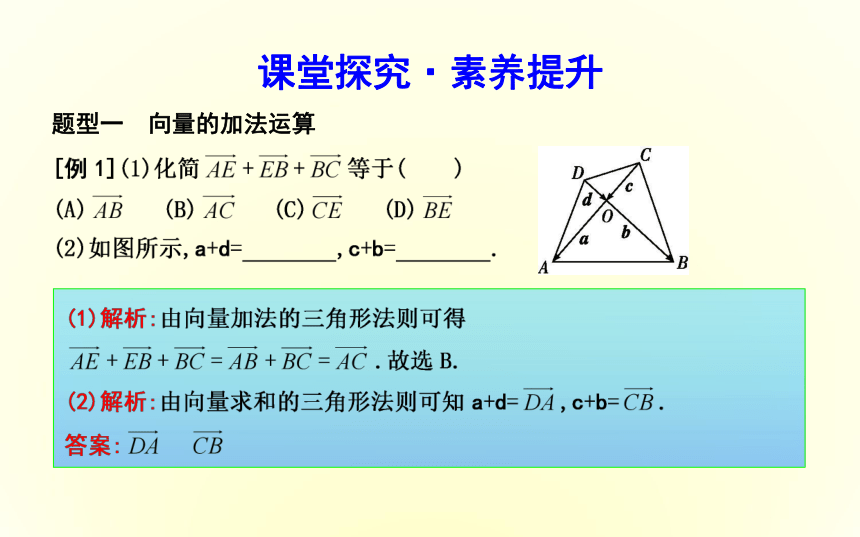
综上可知任意两个向量a,b恒有||a|-|b||≤|a+b|≤|a|+|b|.课堂探究·素养提升题型一 向量的加法运算方法技巧(1)应用三角形法则求向量和的基本步骤(2)应用平行四边形法则求向量和的基本步骤(2)如图所示,已知向量a,b,c,试作出向量a+b+c.题型二 向量加法与平面几何的综合应用
[例2] 已知:如图,四边形ABCD中,AO=OC,DO=OB.
求证:四边形ABCD为平行四边形.方法技巧(1)用向量证明几何问题的一般步骤:
①把几何问题中的边转化成相应的向量;
②通过向量的运算及其几何意义得到向量间的关系;
③还原成几何问题.
(2)要注意有向线段表示的向量相等,说明有向线段所在直线平行或重合且长度相等.互动探究:本例条件不变,求证:△ADO≌△CBO.[备用例2]如图所示,已知E,F分别是?ABCD的边DC,AB的中点,求证:四边形AECF是平行四边形.题型三 向量加法的实际应用
[例3] 一架飞机从A地按北偏东35°的方向飞行800 km到达B地接到受伤人员,然后又从B地按南偏东55°的方向飞行 800 km 送往C地医院,求这架飞机飞行的路程及两次位移的和.方法技巧求解与向量有关的实际问题的解题步骤(2)求船实际航行的速度的大小与方向(用与江水的速度方向间的夹角表示).错解:C正解:B学霸经验分享区(1)三角形法则和平行四边形法则都是求向量和的基本方法,两个法则是统一的.当两个向量首尾相连时常选用三角形法则,当两个向量共始点时,常选用平行四边形法则.
(2)向量的加法满足交换律,因此在进行多个向量的加法运算时,可以按照任意的次序和任意的组合去进行.课堂达标B2.下列命题中正确的个数为( )DD5.已知向量a,b,c,如图,求作a+b+c.点击进入 课时作业
2.2.1 向量加法运算及其几何意义目标导航新知导学课堂探究1.向量加法的定义
定义:求两个向量 的运算,叫做向量的加法.
对于零向量与任一向量a,规定0+a=a+ = .0新知导学·素养养成a和2.向量求和的法则思考1:向量加法的三角形法则和平行四边形法则的使用条件有什么不同?
提示:三角形法则适用于任意两个非零向量求和,平行四边形法则只适用于两个不共线的向量求和.3.向量加法的运算律
(1)交换律:a+b= .
(2)结合律:(a+b)+c= .
4.重要结论
|a+b| |a|+|b|.b+aa+(b+c)≤思考2:(a+b)+(c+d)=(a+d)+(b+c)成立吗?
提示:成立.向量加法满足交换律和结合律,因此在进行多个向量的加法运算时,就可以按照任意的次序和任意的组合进行.名师点津(1)在使用向量加法的三角形法则时,应注意“首尾连接”;在使用平行四边形法则时,应注意范围的限制及和向量与两向量起点相同.
(2)向量a+b与非零向量a,b的模及方向的联系
①当两个非零向量a与b不共线时,由向量加法的三角形法则可知a+b的方向与a,b的方向都不相同,且 ||a|-|b||<|a+b|<|a|+|b|,几何意义是三角形两边之和大于第三边,两边之差小于第三边.
②当两个非零向量a与b共线且同向时(如图1),则向量a+b与a(或b)方向相同,且|a+b|=|a|+|b|.③当两个非零向量a与b反向且|a|<|b|时(如图2),则a+b与b方向相同(与a方向相反),且|a+b|=||a|-|b||.
④当两个向量a与b中至少有一个为0时,则必有|a+b|=|a|+|b|=||a|-|b||.
综上可知任意两个向量a,b恒有||a|-|b||≤|a+b|≤|a|+|b|.课堂探究·素养提升题型一 向量的加法运算方法技巧(1)应用三角形法则求向量和的基本步骤(2)应用平行四边形法则求向量和的基本步骤(2)如图所示,已知向量a,b,c,试作出向量a+b+c.题型二 向量加法与平面几何的综合应用
[例2] 已知:如图,四边形ABCD中,AO=OC,DO=OB.
求证:四边形ABCD为平行四边形.方法技巧(1)用向量证明几何问题的一般步骤:
①把几何问题中的边转化成相应的向量;
②通过向量的运算及其几何意义得到向量间的关系;
③还原成几何问题.
(2)要注意有向线段表示的向量相等,说明有向线段所在直线平行或重合且长度相等.互动探究:本例条件不变,求证:△ADO≌△CBO.[备用例2]如图所示,已知E,F分别是?ABCD的边DC,AB的中点,求证:四边形AECF是平行四边形.题型三 向量加法的实际应用
[例3] 一架飞机从A地按北偏东35°的方向飞行800 km到达B地接到受伤人员,然后又从B地按南偏东55°的方向飞行 800 km 送往C地医院,求这架飞机飞行的路程及两次位移的和.方法技巧求解与向量有关的实际问题的解题步骤(2)求船实际航行的速度的大小与方向(用与江水的速度方向间的夹角表示).错解:C正解:B学霸经验分享区(1)三角形法则和平行四边形法则都是求向量和的基本方法,两个法则是统一的.当两个向量首尾相连时常选用三角形法则,当两个向量共始点时,常选用平行四边形法则.
(2)向量的加法满足交换律,因此在进行多个向量的加法运算时,可以按照任意的次序和任意的组合去进行.课堂达标B2.下列命题中正确的个数为( )DD5.已知向量a,b,c,如图,求作a+b+c.点击进入 课时作业
