人教A版高中数学必修五 课件:1.1.1 正弦定理 :32张PPT
文档属性
| 名称 | 人教A版高中数学必修五 课件:1.1.1 正弦定理 :32张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 20:52:04 | ||
图片预览











文档简介
课件32张PPT。第一章 解三角形
1.1 正弦定理和余弦定理
1.1.1 正弦定理目标导航新知导学课堂探究1.正弦定理
(1)定理:在一个三角形中,各边和它所对角的 的比相等.
(2)表达式: .
思考1:正弦定理对任意三角形都成立吗?正弦新知导学·素养养成思考2:在△ABC中,为什么说A>B等价于sin A>sin B?
答案:由sin A>sin B?2Rsin A>2Rsin B?a>b?A>B.a思考3:利用正弦定理解三角形如何防止漏解或增解?
答案:①要结合平面几何中“大边对大角,大角对大边”及三角形内角和定理去考虑问题.
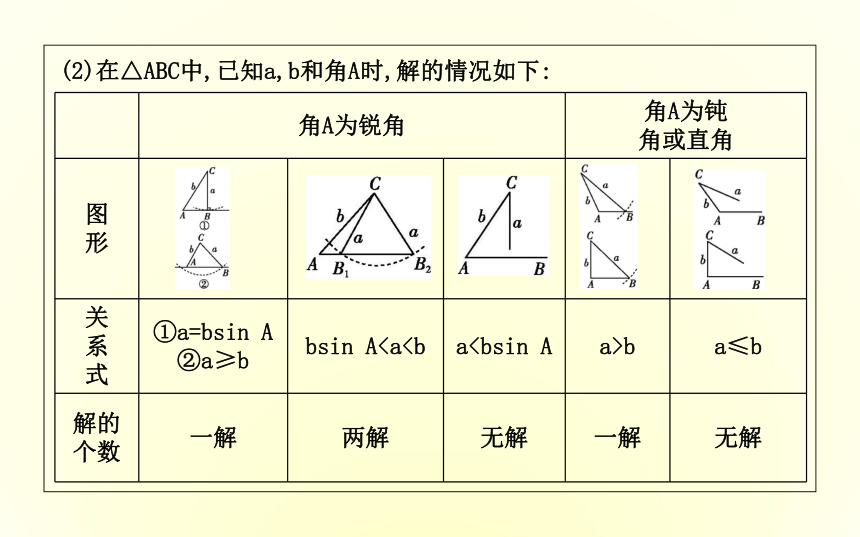
②明确给定的三角形的元素,为了防止漏解或增解,有时常结合几何作图进行判断.2.解三角形一般地,把三角形的三个角A,B,C和它们的对边 , , 叫做三角形的元素,已知三角形的几个元素求其他元素的过程叫做 .bc解三角形名师点津(1)正弦定理的常见变形(R为△ABC外接圆的半径)(2)在△ABC中,已知a,b和角A时,解的情况如下:课堂探究·素养提升题型一 已知两角及一边解三角形答案:(1)A(2)在△ABC中,已知BC=12,∠A=60°,∠B=45°,则AC= .?方法技巧已知三角形两角和任一边解三角形的方法
(1)若所给边是已知角的对边时,可由正弦定理求另一角所对边,再由三角形内角和定理求出第三个角,再由正弦定理求出第三边.
(2)若所给边不是已知角的对边时,先由三角形内角和定理求出第三个角,再由正弦定理求另外两边.即时训练1-1:在△ABC中,A=30°,C=105°,a=2,求B,b,c. [备用例1]在△ABC中,已知a=8,B=60°,C=75°,求A,b,c.题型二 已知两边及其中一边的对角解三角形方法技巧已知三角形中的两边和其中一边的对角,解三角形时:
(1)首先由正弦定理求出另一边对角的正弦值.
(2)如果已知的角为大边所对的角时,由三角形中大边对大角,大角对大边的法则能判断另一边所对的角为锐角,由正弦值可求锐角.
(3)如果已知的角为小边所对的角时,则不能判断另一边所对的角为锐角,这时由正弦值可求两个角,要分类讨论.(2)在△ABC中,已知a2tan B=b2tan A,试判断△ABC的形状.方法技巧(2)化边为角.将题目中所有的条件,利用正弦定理化边为角,再根据三角函数的有关知识得到三个内角的关系,进而确定三角形的形状.利用的公式为a=2Rsin A,b=2Rsin B,c=2Rsin C.即时训练3-1:在△ABC中,sin2A=sin2B+sin2C,且sin A=2sin Bcos C.试判断△ABC的形状.(2)在利用正弦定理解三角形或判断三角形的形状时应注意角的范围这一隐含条件,即三角形的内角在(0°,180°)范围内,同时应结合三角函数的有关公式进行综合分析.学霸经验分享区(1)在三角形中,解决有关含有边角关系的问题时常运用正弦定理化边为角(或化角为边),然后利用三角函数知识解决.
(2)角变换时变换方法及公式都要熟练掌握,同时应注意三角形中各角的范围.
(3)应用正弦定理解三角形时的常用结论
①在△ABC中,a+b>c,|a-b|sin C.
②在△ABC中,a>b?A>B?sin A>sin B.课堂达标B1.有关正弦定理的叙述:①正弦定理只适用于锐角三角形;②正弦定理不适用于直角三角形;③在某一确定的三角形中,各边与它所对角的正弦的比是一定值;④在△ABC中,sin A∶sin B∶sin C=a∶b∶c.其中正确的个数是( )
(A)1 (B)2 (C)3 (D)4解析:正弦定理适用于任意三角形,故①②均不正确;由正弦定理可知,三角形一旦确定,则各边与其所对角的正弦的比就确定了,故③正确;由比例性质和正弦定理可推知④正确.故选B.C 3.(2019·湖南长沙检测)在△ABC中,已知b=40,c=20,C=60°,则此三角形的解的情况是( )
(A)有一解
(B)有两解
(C)无解
(D)有解,但解的个数不确定C答案:60°或120°5.(2019·辽宁锦州月考)在△ABC中,a,b,c分别是内角A,B,C所对的边,若ccos A=b,则△ABC的形状为 .?答案:直角三角形
1.1 正弦定理和余弦定理
1.1.1 正弦定理目标导航新知导学课堂探究1.正弦定理
(1)定理:在一个三角形中,各边和它所对角的 的比相等.
(2)表达式: .
思考1:正弦定理对任意三角形都成立吗?正弦新知导学·素养养成思考2:在△ABC中,为什么说A>B等价于sin A>sin B?
答案:由sin A>sin B?2Rsin A>2Rsin B?a>b?A>B.a思考3:利用正弦定理解三角形如何防止漏解或增解?
答案:①要结合平面几何中“大边对大角,大角对大边”及三角形内角和定理去考虑问题.
②明确给定的三角形的元素,为了防止漏解或增解,有时常结合几何作图进行判断.2.解三角形一般地,把三角形的三个角A,B,C和它们的对边 , , 叫做三角形的元素,已知三角形的几个元素求其他元素的过程叫做 .bc解三角形名师点津(1)正弦定理的常见变形(R为△ABC外接圆的半径)(2)在△ABC中,已知a,b和角A时,解的情况如下:课堂探究·素养提升题型一 已知两角及一边解三角形答案:(1)A(2)在△ABC中,已知BC=12,∠A=60°,∠B=45°,则AC= .?方法技巧已知三角形两角和任一边解三角形的方法
(1)若所给边是已知角的对边时,可由正弦定理求另一角所对边,再由三角形内角和定理求出第三个角,再由正弦定理求出第三边.
(2)若所给边不是已知角的对边时,先由三角形内角和定理求出第三个角,再由正弦定理求另外两边.即时训练1-1:在△ABC中,A=30°,C=105°,a=2,求B,b,c. [备用例1]在△ABC中,已知a=8,B=60°,C=75°,求A,b,c.题型二 已知两边及其中一边的对角解三角形方法技巧已知三角形中的两边和其中一边的对角,解三角形时:
(1)首先由正弦定理求出另一边对角的正弦值.
(2)如果已知的角为大边所对的角时,由三角形中大边对大角,大角对大边的法则能判断另一边所对的角为锐角,由正弦值可求锐角.
(3)如果已知的角为小边所对的角时,则不能判断另一边所对的角为锐角,这时由正弦值可求两个角,要分类讨论.(2)在△ABC中,已知a2tan B=b2tan A,试判断△ABC的形状.方法技巧(2)化边为角.将题目中所有的条件,利用正弦定理化边为角,再根据三角函数的有关知识得到三个内角的关系,进而确定三角形的形状.利用的公式为a=2Rsin A,b=2Rsin B,c=2Rsin C.即时训练3-1:在△ABC中,sin2A=sin2B+sin2C,且sin A=2sin Bcos C.试判断△ABC的形状.(2)在利用正弦定理解三角形或判断三角形的形状时应注意角的范围这一隐含条件,即三角形的内角在(0°,180°)范围内,同时应结合三角函数的有关公式进行综合分析.学霸经验分享区(1)在三角形中,解决有关含有边角关系的问题时常运用正弦定理化边为角(或化角为边),然后利用三角函数知识解决.
(2)角变换时变换方法及公式都要熟练掌握,同时应注意三角形中各角的范围.
(3)应用正弦定理解三角形时的常用结论
①在△ABC中,a+b>c,|a-b|
②在△ABC中,a>b?A>B?sin A>sin B.课堂达标B1.有关正弦定理的叙述:①正弦定理只适用于锐角三角形;②正弦定理不适用于直角三角形;③在某一确定的三角形中,各边与它所对角的正弦的比是一定值;④在△ABC中,sin A∶sin B∶sin C=a∶b∶c.其中正确的个数是( )
(A)1 (B)2 (C)3 (D)4解析:正弦定理适用于任意三角形,故①②均不正确;由正弦定理可知,三角形一旦确定,则各边与其所对角的正弦的比就确定了,故③正确;由比例性质和正弦定理可推知④正确.故选B.C 3.(2019·湖南长沙检测)在△ABC中,已知b=40,c=20,C=60°,则此三角形的解的情况是( )
(A)有一解
(B)有两解
(C)无解
(D)有解,但解的个数不确定C答案:60°或120°5.(2019·辽宁锦州月考)在△ABC中,a,b,c分别是内角A,B,C所对的边,若ccos A=b,则△ABC的形状为 .?答案:直角三角形
