人教A版高中数学必修五 课件:第1章末总结 :26张PPT
文档属性
| 名称 | 人教A版高中数学必修五 课件:第1章末总结 :26张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 21:07:17 | ||
图片预览



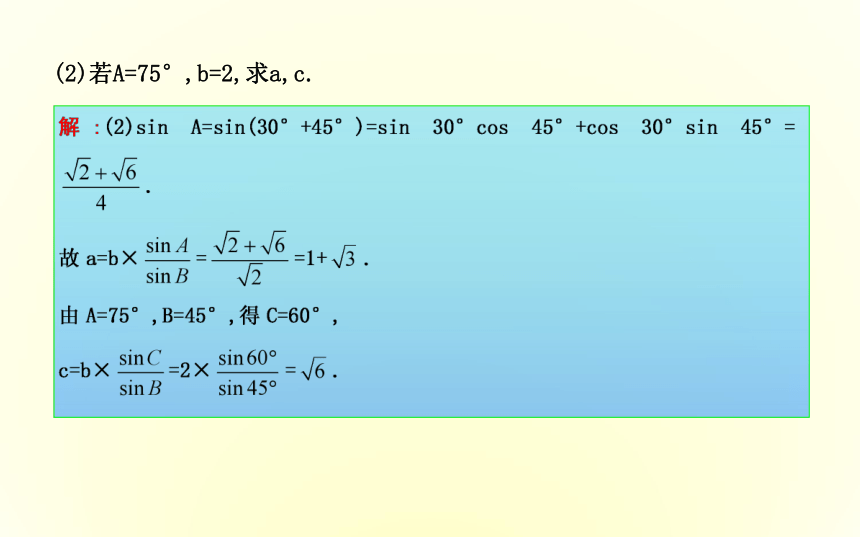




文档简介
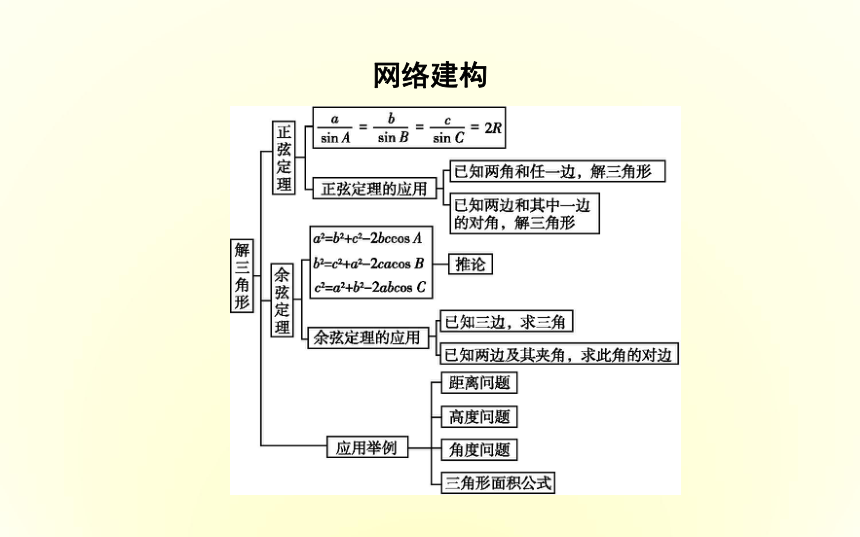
课件26张PPT。章末总结网络建构知识辨析判断下列说法是否正确.(请在括号中填“√”或“×”)
1.正弦定理和余弦定理揭示了任意三角形边角之间的关系,因此,它适应于任何三角形.( )
2.在△ABC中,等式bsin A=asin B总能成立.( )
3.在△ABC中,已知a,b,A,则此三角形有唯一解.( )
4.在△ABC中,若a2>b2+c2,则△ABC一定为钝角三角形.( )
5.在△ABC中,已知两边和其夹角时,△ABC不唯一.( )
6.方位角和方向角是一样的.( )
7.公式S= absin C适合求任意三角形的面积.( )
8.三角形中已知三边无法求其面积.( )√√×√××√×题型探究·素养提升题型一 利用正、余弦定理解三角形(2)若A=75°,b=2,求a,c.规律总结运用正、余弦定理解三角形的策略
在解三角形时,常常将正、余弦定理结合在一起使用,要注意恰当选取定理,简化运算过程,提高解题速度.解题时要综合、灵活地运用这两个定理,认真分析已知条件,结合三角形的有关性质(如大角对大边,大边对大角,三角形内角和定理等),并注意数形结合,防止出现漏解或增解的情况. 题型二 利用正、余弦定理判断三角形的形状
[典例2] (2019·杭州高二检测)已知△ABC的三个内角A,B,C的对边分别为a,b,c,满足a+c=2b且2cos 2B-8cos B+5=0,求B的大小并判断△ABC的形状.规律总结判断三角形的形状策略
欲判断三角形的形状特征,不仅要深入研究三角形的边与边的大小关系,还要研究角与角的大小关系.解这类问题的思考方法是:从条件出发,利用正弦定理(或余弦定理)进行代换转化,逐步将给出的式子化为纯粹的边与边的关系或角与角的关系,通过运算求出边或角的大小,或者确定边与边或角与角的等量关系,从而正确判定三角形的形状.(2)求a,b的值.规律总结(2)在涉及三角形面积时,常常借助正弦定理或余弦定理进行边和角的转化.规律总结解三角形应用题的步骤
(1)准确地理解题意;(2)正确地作出图形(或准确地理解图形);(3)把已知和要求的量尽量集中在有关三角形中,利用正弦定理和余弦定理有顺序地解这些三角形;(4)根据实际意义和精确度的要求给出答案.真题体验AC4.(2018·全国Ⅰ卷)△ABC的内角A,B,C的对边分别为a,b,c,已知bsin C +csin B=4asin Bsin C,b2+c2-a2=8,则△ABC的面积为 .?5.(2018·全国Ⅰ卷)在平面四边形ABCD中,∠ADC=90°,∠A=45°,AB=2, BD=5.
(1)求cos∠ADB;(2)设a=2,c=3,求b和sin(2A-B)的值.
1.正弦定理和余弦定理揭示了任意三角形边角之间的关系,因此,它适应于任何三角形.( )
2.在△ABC中,等式bsin A=asin B总能成立.( )
3.在△ABC中,已知a,b,A,则此三角形有唯一解.( )
4.在△ABC中,若a2>b2+c2,则△ABC一定为钝角三角形.( )
5.在△ABC中,已知两边和其夹角时,△ABC不唯一.( )
6.方位角和方向角是一样的.( )
7.公式S= absin C适合求任意三角形的面积.( )
8.三角形中已知三边无法求其面积.( )√√×√××√×题型探究·素养提升题型一 利用正、余弦定理解三角形(2)若A=75°,b=2,求a,c.规律总结运用正、余弦定理解三角形的策略
在解三角形时,常常将正、余弦定理结合在一起使用,要注意恰当选取定理,简化运算过程,提高解题速度.解题时要综合、灵活地运用这两个定理,认真分析已知条件,结合三角形的有关性质(如大角对大边,大边对大角,三角形内角和定理等),并注意数形结合,防止出现漏解或增解的情况. 题型二 利用正、余弦定理判断三角形的形状
[典例2] (2019·杭州高二检测)已知△ABC的三个内角A,B,C的对边分别为a,b,c,满足a+c=2b且2cos 2B-8cos B+5=0,求B的大小并判断△ABC的形状.规律总结判断三角形的形状策略
欲判断三角形的形状特征,不仅要深入研究三角形的边与边的大小关系,还要研究角与角的大小关系.解这类问题的思考方法是:从条件出发,利用正弦定理(或余弦定理)进行代换转化,逐步将给出的式子化为纯粹的边与边的关系或角与角的关系,通过运算求出边或角的大小,或者确定边与边或角与角的等量关系,从而正确判定三角形的形状.(2)求a,b的值.规律总结(2)在涉及三角形面积时,常常借助正弦定理或余弦定理进行边和角的转化.规律总结解三角形应用题的步骤
(1)准确地理解题意;(2)正确地作出图形(或准确地理解图形);(3)把已知和要求的量尽量集中在有关三角形中,利用正弦定理和余弦定理有顺序地解这些三角形;(4)根据实际意义和精确度的要求给出答案.真题体验AC4.(2018·全国Ⅰ卷)△ABC的内角A,B,C的对边分别为a,b,c,已知bsin C +csin B=4asin Bsin C,b2+c2-a2=8,则△ABC的面积为 .?5.(2018·全国Ⅰ卷)在平面四边形ABCD中,∠ADC=90°,∠A=45°,AB=2, BD=5.
(1)求cos∠ADB;(2)设a=2,c=3,求b和sin(2A-B)的值.
