人教A版高中数学必修五 课件:3.2 第一课时 一元二次不等式及其解法 :37张PPT
文档属性
| 名称 | 人教A版高中数学必修五 课件:3.2 第一课时 一元二次不等式及其解法 :37张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 21:32:09 | ||
图片预览











文档简介
课件37张PPT。3.2 一元二次不等式及其解法
第一课时 一元二次不等式及其解法[目标导航]新知导学课堂探究1.一元二次不等式
只含有 未知数,并且未知数的最高次数是 的不等式,叫做一元二次不等式.新知导学·素养养成思考1:不等式ax2+5x+1>0是关于“x”的二次不等式吗?
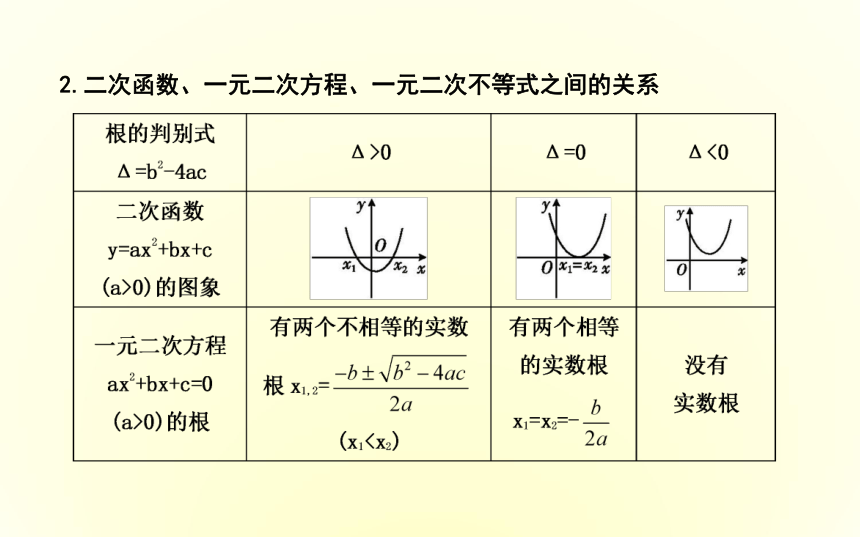
答案:不等式ax2+5x+1>0不一定是一元二次不等式,当a=0时,它是一元一次不等式;若题目中给出的条件是“一元二次不等式ax2+5x+1>0”,则隐含的条件是a≠0.一个22.二次函数、一元二次方程、一元二次不等式之间的关系思考2:若方程ax2+bx+c=0(a≠0)的两根为x1=1,x2=3,那么不等式ax2+bx+
c>0(a≠0)的解集是{x|x<1或x>3}吗?
答案:不一定.当a>0时,其解集为{x|x<1或x>3};当a<0时,其解集为{x|1<
x<3}.名师点津从两个角度看三个“二次”之间的内在联系
(1)函数的角度:一元二次不等式ax2+bx+c>0表示二次函数y=ax2+bx+c的函数值大于0,图象在x轴的上方;一元二次不等式ax2+bx+c>0的解集即二次函数图象在x轴上方部分的自变量的取值范围.(2)方程的角度:一元二次不等式ax2+bx+c>0的解集的端点值是一元二次方程ax2+bx+c=0的根.课堂探究·素养提升题型一 解不含参数的一元二次不等式[例1]求下列一元二次不等式的解集.
(1)9x2-6x+1≤0;解:(2)由-x2+2x>3得x2-2x+3<0,
方程x2-2x+3=0的判别式Δ=4-12<0,
所以方程x2-2x+3=0无实根,
所以原不等式的解集为 .
(3)由x2-2x+1>0得(x-1)2>0,
方程(x-1)2=0的根为x=1,
所以不等式x2-2x+1>0的解集为{x|x≠1}.(2)-x2+2x>3;
(3)x2-2x+1>0.方法技巧解不含参数的一元二次不等式的一般步骤
(1)化标准.通过对不等式的变形,使不等式右侧为0,使二次项系数为正.(2)判别式.对不等式左侧因式分解,若不易分解,则计算对应方程根的判别式.
(3)求实根.求出相应的一元二次方程的根或根据判别式说明方程有无实根.
(4)画草图.根据一元二次方程根的情况画出对应的二次函数的草图.
(5)写解集.根据图象写出不等式的解集.即时训练1-1:求下列一元二次不等式的解集.
(1)x2-5x>6;
(2)x2-6x+9≤0;
(3)-x2+2x+8>0.解:(1)由x2-5x>6,得x2-5x-6>0.因为x2-5x-6=0的两根是x=-1或6,
所以原不等式的解集为{x|x<-1或x>6}.
(2)由x2-6x+9≤0得(x-3)2≤0,所以原不等式的解集为{x|x=3}.
(3)原不等式可化为x2-2x-8<0,
又Δ=(-2)2-4×(-8)=36>0,
所以方程x2-2x-8=0有两个不等实根x1=-2,x2=4,
所以原不等式的解集为{x|-20},则M∩N为( )
(A){x|-4≤x<-2或3(B){x|-4(C){x|x≤-2或x>3}
(D){x|x<-2或x≥3}解析:(1)因为M={x|x2-3x-28≤0}={x|-4≤x≤7},
N={x|x2-x-6>0}={x|x<-2或x>3},
所以M∩N={x|-4≤x<-2或3(A)(-∞,-2)∪[0,+∞)
(B)(-∞,-6]∪(2,+∞)
(C)(-∞,-2]∪[0,+∞)
(D)(-∞,-6)∪[2,+∞)题型二 解含参数的一元二次不等式[例2]解关于x的不等式:ax2+(1-a)x-1>0.规范解答:原不等式可化为(x-1)(ax+1)>0.
(1)当a=0时,原不等式为x-1>0,
所以解集为{x|x>1}.方法技巧解含参数的一元二次不等式时要对参数分类讨论
(1)讨论二次项系数,按二次项系数等于零、大于零、小于零三种情况进行分类;(2)讨论根的判别式Δ>0,Δ=0,Δ<0;
(3)讨论根的大小.讨论顺序可简记为“一a,二Δ,三两根大小”.即时训练2-1:解关于x的不等式x2-2ax-8a2<0.解:不等式x2-2ax-8a2<0可化为(x+2a)(x-4a)<0.
(1)当-2a=4a,即a=0时,不等式即为x2<0,解集为 ;
(2)当-2a>4a,即a<0时,则4a(3)当-2a<4a,即a>0时,则-2a综上所述,当a=0时,原不等式的解集为 ;
当a<0时,原不等式解集为{x|4a当a>0时,原不等式解集为{x|-2a0.解:(1)将不等式x2-(a+a2)x+a3>0变形为(x-a)(x-a2)>0.
因为a2-a=a(a-1),
所以当a<0或a>1时,a解集为{x|xa2}.
当0a}.
当a=0或1时,解集为{x|x∈R且x≠a}.
综上知,当a<0或a>1时,不等式的解集为{x|xa2};
当0a};
当a=0或1时,不等式的解集为{x|x∈R或x≠a}.(2)解关于x的不等式2x2+kx-k≤0.题型三 可化为一元二次不等式的简单分式不等式方法技巧即时训练3-1:(2019·临沂高二检测)不等式 <3的解集是 .[备用例3](1)(2019·广东深圳摸底)不等式 ≤x-1的解集是( )
(A)(-∞,-1)∪(1,3] (B)[-1,1)∪[3,+∞)
(C)[1,3) (D)(-∞,1]∪(3,+∞)(1)解析:当x-1>0,即x>1时,不等式可化为4≤(x-1)2,即x-1≤-2或x-1≥2,解得x≤-1或x≥3.故此时的解集为{x|x≥3}.
当x-1<0,即x<1时,不等式可化为4≥(x-1)2,
即-2≤x-1≤2,解得-1≤x≤3.
故此时的解集为{x|-1≤x<1}.
综上,不等式的解集为[-1,1)∪[3,+∞).故选B.(2)(2019·齐鲁名校调研)函数y=ln( -1)的定义域为( )
(A)(0,1) (B)(1,+∞)
(C)(-∞,0)∪(1,+∞) (D)(-∞,1)题型四 易错辨析——忽略二次项系数的符号致误[例4]解不等式-6x2-x+2≥0.纠错:没有注意到二次项系数小于0这个情况,此时应先把二次项系数化为正数,再进行求解.学霸经验分享区(1)对于一元二次不等式ax2+bx+c>0(a>0)或ax2+bx+c<0(a>0)的求解,要善于联想两个方面的问题:①二次函数y=ax2+bx+c与x轴的交点及图象.②方程ax2+bx+c=0的根.
(2)含有参数的不等式的求解,要注意按某一恰当的分类标准进行
讨论.课堂达标解析:解不等式得-1≤x≤0.故选D.D1.不等式x(x+1)≤0的解集为( )
(A)[-1,+∞) (B)[-1,0)
(C)(- ∞,-1] (D)[-1,0]2.不等式 <0的解集为( )
(A)(1,+∞)
(B)(-∞,-2)
(C)(-2,1)
(D)(-∞,-2)∪(1,+∞)C解析:原不等式化为(x-1)(x+2)<0,解得-2所以原不等式的解集为(-2,1).故选C.3.不等式2x≤x2+1的解集为( )
(A) (B)R
(C){x|x≠1} (D){x|x>1或x<-1}B解析:2x≤x2+1?x2-2x+1≥0?(x-1)2≥0,
所以x∈R.故选B.4.不等式x2-ax-12a2<0(其中a<0)的解集为 .?解析:方程x2-ax-12a2=0的两根为4a,-3a,
且4a<-3a,
所以所求不等式的解集为{x|4a1的解集为 .? 点击进入 课时作业
第一课时 一元二次不等式及其解法[目标导航]新知导学课堂探究1.一元二次不等式
只含有 未知数,并且未知数的最高次数是 的不等式,叫做一元二次不等式.新知导学·素养养成思考1:不等式ax2+5x+1>0是关于“x”的二次不等式吗?
答案:不等式ax2+5x+1>0不一定是一元二次不等式,当a=0时,它是一元一次不等式;若题目中给出的条件是“一元二次不等式ax2+5x+1>0”,则隐含的条件是a≠0.一个22.二次函数、一元二次方程、一元二次不等式之间的关系思考2:若方程ax2+bx+c=0(a≠0)的两根为x1=1,x2=3,那么不等式ax2+bx+
c>0(a≠0)的解集是{x|x<1或x>3}吗?
答案:不一定.当a>0时,其解集为{x|x<1或x>3};当a<0时,其解集为{x|1<
x<3}.名师点津从两个角度看三个“二次”之间的内在联系
(1)函数的角度:一元二次不等式ax2+bx+c>0表示二次函数y=ax2+bx+c的函数值大于0,图象在x轴的上方;一元二次不等式ax2+bx+c>0的解集即二次函数图象在x轴上方部分的自变量的取值范围.(2)方程的角度:一元二次不等式ax2+bx+c>0的解集的端点值是一元二次方程ax2+bx+c=0的根.课堂探究·素养提升题型一 解不含参数的一元二次不等式[例1]求下列一元二次不等式的解集.
(1)9x2-6x+1≤0;解:(2)由-x2+2x>3得x2-2x+3<0,
方程x2-2x+3=0的判别式Δ=4-12<0,
所以方程x2-2x+3=0无实根,
所以原不等式的解集为 .
(3)由x2-2x+1>0得(x-1)2>0,
方程(x-1)2=0的根为x=1,
所以不等式x2-2x+1>0的解集为{x|x≠1}.(2)-x2+2x>3;
(3)x2-2x+1>0.方法技巧解不含参数的一元二次不等式的一般步骤
(1)化标准.通过对不等式的变形,使不等式右侧为0,使二次项系数为正.(2)判别式.对不等式左侧因式分解,若不易分解,则计算对应方程根的判别式.
(3)求实根.求出相应的一元二次方程的根或根据判别式说明方程有无实根.
(4)画草图.根据一元二次方程根的情况画出对应的二次函数的草图.
(5)写解集.根据图象写出不等式的解集.即时训练1-1:求下列一元二次不等式的解集.
(1)x2-5x>6;
(2)x2-6x+9≤0;
(3)-x2+2x+8>0.解:(1)由x2-5x>6,得x2-5x-6>0.因为x2-5x-6=0的两根是x=-1或6,
所以原不等式的解集为{x|x<-1或x>6}.
(2)由x2-6x+9≤0得(x-3)2≤0,所以原不等式的解集为{x|x=3}.
(3)原不等式可化为x2-2x-8<0,
又Δ=(-2)2-4×(-8)=36>0,
所以方程x2-2x-8=0有两个不等实根x1=-2,x2=4,
所以原不等式的解集为{x|-2
(A){x|-4≤x<-2或3
(D){x|x<-2或x≥3}解析:(1)因为M={x|x2-3x-28≤0}={x|-4≤x≤7},
N={x|x2-x-6>0}={x|x<-2或x>3},
所以M∩N={x|-4≤x<-2或3
(B)(-∞,-6]∪(2,+∞)
(C)(-∞,-2]∪[0,+∞)
(D)(-∞,-6)∪[2,+∞)题型二 解含参数的一元二次不等式[例2]解关于x的不等式:ax2+(1-a)x-1>0.规范解答:原不等式可化为(x-1)(ax+1)>0.
(1)当a=0时,原不等式为x-1>0,
所以解集为{x|x>1}.方法技巧解含参数的一元二次不等式时要对参数分类讨论
(1)讨论二次项系数,按二次项系数等于零、大于零、小于零三种情况进行分类;(2)讨论根的判别式Δ>0,Δ=0,Δ<0;
(3)讨论根的大小.讨论顺序可简记为“一a,二Δ,三两根大小”.即时训练2-1:解关于x的不等式x2-2ax-8a2<0.解:不等式x2-2ax-8a2<0可化为(x+2a)(x-4a)<0.
(1)当-2a=4a,即a=0时,不等式即为x2<0,解集为 ;
(2)当-2a>4a,即a<0时,则4a
当a<0时,原不等式解集为{x|4a
因为a2-a=a(a-1),
所以当a<0或a>1时,a
当0
当a=0或1时,解集为{x|x∈R且x≠a}.
综上知,当a<0或a>1时,不等式的解集为{x|x
当0
当a=0或1时,不等式的解集为{x|x∈R或x≠a}.(2)解关于x的不等式2x2+kx-k≤0.题型三 可化为一元二次不等式的简单分式不等式方法技巧即时训练3-1:(2019·临沂高二检测)不等式 <3的解集是 .[备用例3](1)(2019·广东深圳摸底)不等式 ≤x-1的解集是( )
(A)(-∞,-1)∪(1,3] (B)[-1,1)∪[3,+∞)
(C)[1,3) (D)(-∞,1]∪(3,+∞)(1)解析:当x-1>0,即x>1时,不等式可化为4≤(x-1)2,即x-1≤-2或x-1≥2,解得x≤-1或x≥3.故此时的解集为{x|x≥3}.
当x-1<0,即x<1时,不等式可化为4≥(x-1)2,
即-2≤x-1≤2,解得-1≤x≤3.
故此时的解集为{x|-1≤x<1}.
综上,不等式的解集为[-1,1)∪[3,+∞).故选B.(2)(2019·齐鲁名校调研)函数y=ln( -1)的定义域为( )
(A)(0,1) (B)(1,+∞)
(C)(-∞,0)∪(1,+∞) (D)(-∞,1)题型四 易错辨析——忽略二次项系数的符号致误[例4]解不等式-6x2-x+2≥0.纠错:没有注意到二次项系数小于0这个情况,此时应先把二次项系数化为正数,再进行求解.学霸经验分享区(1)对于一元二次不等式ax2+bx+c>0(a>0)或ax2+bx+c<0(a>0)的求解,要善于联想两个方面的问题:①二次函数y=ax2+bx+c与x轴的交点及图象.②方程ax2+bx+c=0的根.
(2)含有参数的不等式的求解,要注意按某一恰当的分类标准进行
讨论.课堂达标解析:解不等式得-1≤x≤0.故选D.D1.不等式x(x+1)≤0的解集为( )
(A)[-1,+∞) (B)[-1,0)
(C)(- ∞,-1] (D)[-1,0]2.不等式 <0的解集为( )
(A)(1,+∞)
(B)(-∞,-2)
(C)(-2,1)
(D)(-∞,-2)∪(1,+∞)C解析:原不等式化为(x-1)(x+2)<0,解得-2
(A) (B)R
(C){x|x≠1} (D){x|x>1或x<-1}B解析:2x≤x2+1?x2-2x+1≥0?(x-1)2≥0,
所以x∈R.故选B.4.不等式x2-ax-12a2<0(其中a<0)的解集为 .?解析:方程x2-ax-12a2=0的两根为4a,-3a,
且4a<-3a,
所以所求不等式的解集为{x|4a
