人教A版高中数学必修五 课件:3.3.2 第二课时 简单线性规划的应用 :48张PPT
文档属性
| 名称 | 人教A版高中数学必修五 课件:3.3.2 第二课时 简单线性规划的应用 :48张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 00:00:00 | ||
图片预览











文档简介
课件48张PPT。第二课时 简单线性规划的应用[目标导航]题型一 求最大值的实际应用问题课堂探究·素养提升[例1]某公司计划在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟,假定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?规范解答:设该公司在甲电视台和乙电视台做广告的时间分别为x分钟和y分钟,总收益为z元,由题意得规律总结利用线性规划解决实际问题的步骤
(1)设出未知数(当数据较多时,可以列表格来分析数据);(2)列出约束条件,确立目标函数;(3)作出可行域;(4)利用图解法求出最优解;(5)得出结论.即时训练1-1:某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨.销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨,求该企业在一个生产周期内可获得的最大利润.解:设生产甲产品x吨,生产乙产品y吨,则有关系[备用例1](1)某公司计划同时出售电子琴和洗衣机,由于两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力等)确定产品的月供应量,以使得总利润达到最大,已知对这两种产品有直接限制的因素是资金和劳动力,通过调查,得到关于两种产品的有关数据如下表:试问:怎样确定两种货的供应量,才能使总利润最大,最大利润是多少?(2)(2016·天津卷)某化肥厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料.生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示:现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.分别用x,y表示计划生产甲、乙两种肥料的车皮数.
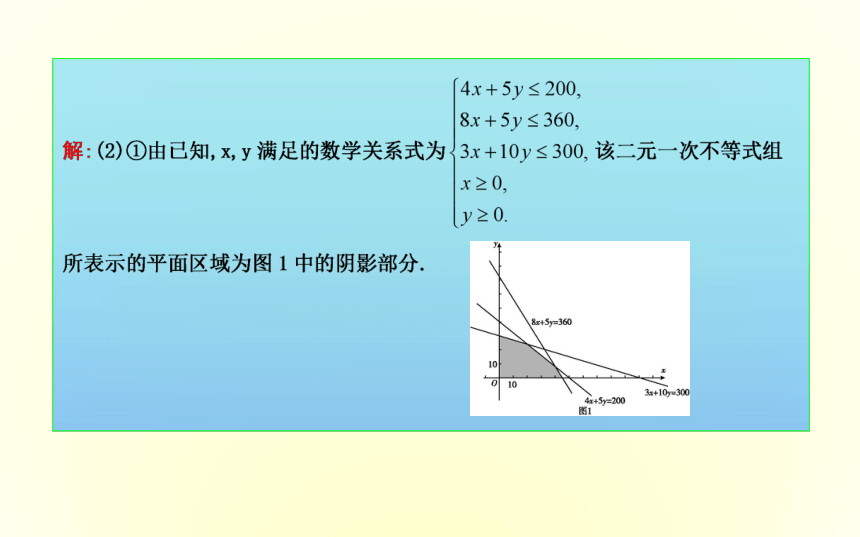
①用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;②问分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?并求出此最大利润.题型二 求最小值的实际应用问题[例2](2019·山东菏泽检测)某公司的仓库A存有货物12 t, 仓库B存有货物8 t.现按7 t,8 t和5 t把货物分别调运给甲、乙、丙三个商店,从仓库A运货物到商店甲、乙、丙,每吨货物的运费分别为8元、6元、9元;从仓库B运货物到商店甲、乙、丙,每吨货物的运费分别为3元、4元、5元.应如何安排调运方案,才能使得从两个仓库运货物到三个商店的总运费最少?可行域如图所示.
作直线l:x-2y=0,把直线l平行移动,当直线l移至点A(0,8)时,z=x-2y+126取得最小值, zmin=0-2×8+126=110,即x=0,y=8时,总运费最少.
即仓库A运给甲、乙、丙商店的货物分别为0 t,8 t,4 t,仓库B运给甲、乙、丙商店的货物分别为7 t,0 t,1 t,此时可使得从两个仓库运货物到三个商店的总运费最少.方法技巧解答线性规划应用题应注意以下几点:
(1)在线性规划问题的应用中,常常是题中的条件较多,因此认真审题非常重要;(2)线性约束条件中有无等号要依据条件加以判断;
(3)结合实际问题,分析未知数x,y等是否有限制,如x,y为正整数、非负数等;
(4)分清线性约束条件和线性目标函数,线性约束条件一般是不等式,而线性目标函数却是一个等式.即时训练2-1:某人承揽一项业务,需做文字标牌4个,绘画标牌5个,现有两种规格的原料,甲种规格每张3 m2,可做文字标牌1个,绘画标牌2个;乙种规格每张2 m2,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张,才能使得总用料面积最小.所用原料的总面积为z=3x+2y,
作出可行域如图.
在一组平行直线3x+2y=z中,
经过可行域内的点且到原点距离最近的直线.
此直线过直线2x+y=5和直线x+2y=4的交点(2,1).
所以最优解为x=2,y=1,
所以使用甲种规格原料2张,乙种规格原料1张,可使总的用料面积最小.题型三 实际问题中的整数解问题[例3](2019·河南郑州检测)某人有一幢房子,室内面积共180 m2,拟分隔成两类房间作为游客住房.大房间每间面积为18 m2,可住游客5名,每名游客每天住宿费为 40元;小房间每间面积为15 m2,可住游客3名,每名游客每天住宿费为50元;装修大房间每间需1 000元,装修小房间每间需600元.如果他只能筹款8 000元用于装修,且游客能住满客房,他应隔出大房间和小房间各多少间,才能获得最大收益?方法技巧对于线性规划中最优整数解的问题,当解方程组得到的解不是整数解时,可用下面的方法求解:
(1)平移直线法:先在可行域内打网格,再描整点,平移直线l,最先经过或最后经过的整点坐标是整点最优解.(2)检验优值法:当可行域内整点个数较少时,也可将整点坐标逐一代入目标函数求值,经比较得出最优解.
(3)调整优值法:先求非整点最优解及最优值,再借助不定方程知识调整最优值,最后筛选出最优解.即时训练3-1:某运输公司接受了向抗洪抢险地方每天至少运送180吨支援物资的任务,该公司有8辆载重为6吨的A型卡车与4辆载重为10吨的B型卡车,有10名驾驶员,每辆卡车每天往返的次数是A型卡车为4次,B型卡车为3次.每辆卡车每天往返的成本费为A型卡车为320元,B型卡车为504元,请你为该公司调配车辆,使公司所花成本费最低.作直线l′:320x+504y=0.
作一组与l′平行的直线l:
320x+504y=t(t∈R),
由题设x,y是可行域内的整点的横、纵坐标.
在可行域内的整点中,点(8,0)使t取最小值,
即当l过点(8,0)时,t最小,
即zmin=8×320=2 560.
答:每天从公司调A型卡车8辆就能完成任务,且公司所花成本费最低.[备用例2](2019·山东烟台高二检测)某营养师要为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C.如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和
晚餐?则z在可行域的四个顶点A(9,0),B(4,3),C(2,5),D(0,8)处的值分别是
zA=2.5×9+4×0=22.5,
zB=2.5×4+4×3=22,
zC=2.5×2+4×5=25,
zD=2.5×0+4×8=32.
zB最小,
因此,应当为该儿童预订4个单位的午餐和3个单位的晚餐,就可满足
要求.题型四 易错辨析——寻找可行域内整点致误纠错:(1)本题错误的原因是①没能准确作出一组平行直线y=-x+z;②可行域内的整点寻找不准确.
(2)准确作图,充分考虑实际问题的特殊性.当图上的整点不好分辨时,应将几个有可能符合题意的整点的坐标都求出来然后逐一检验,而不能采取“四舍五入”的办法.目标函数为z=x+y,
作一组平行直线y=-x+z,
经过可行域内的点且和原点距离最大的直线必为过点B(8,0)的直线,这时x+y=8.
因为x,y均为正整数,
所以(8,0)不是最优解.
在可行域内找整点,使x+y=7.
经验证,可知点(2,5),(3,4),(4,3),(5,2),(6,1)均为最优解.
答:每根钢管截500 mm的毛坯两根,600 mm的毛坏五根,或截500 mm的毛坯三根,600 mm的毛坯四根,或截500 mm的毛坯四根,600 mm的毛坯三根,或截500 mm的毛坯五根,600 mm的毛坯两根,或截500 mm的毛坯六根,600 mm的毛坯一根最合理.学霸经验分享区(1)利用线性规划求最大值、最小值问题,主要是利润最大、效率最高、省工、省材料等问题,要将求最值的变量设为z,将z表示成其他变量的函数,求其最大值或最小值.(2)对于线性规划问题,由于题干太长,数据太多,为便于理清数据间的关系,不妨用列表法.
(3)在实际应用问题中,有些最优解往往需要整数解(比如人数、车辆数等)而直接根据约束条件得到的不一定是整数解,可以运用枚举法验证求最优整数解,或者运用平移直线求最优整数解.最优整数解有时并非只有一个,应具体情况具体分析.课堂达标解析:由题意,要运送最多的货物,先找到两类型汽车运送的总货物量,即z=6x+4y.选A.1.现有5辆载重6吨的汽车,4辆载重4吨的汽车,设需x辆载重6吨汽车和y辆载重4吨汽车,要运送最多的货物,完成这项运输任务的线性目标函数为( )
(A)z=6x+4y (B)z=5x+4y
(C)z=x+y (D)z=4x+5yA2.某服装制造商有10 m2的棉布料,10 m2的羊毛料和6 m2的丝绸料,做一条裤子需要1 m2的棉布料,2 m2的羊毛料和1 m2的丝绸料,做一条裙子需要1 m2的棉布料,1 m2的羊毛料和1 m2的丝绸料,做一条裤子的纯收益是 20元,一条裙子的纯收益是40元,为了使收益达到最大,若生产裤子x条,裙子y条,利润为z元,则生产这两种服装所满足的数学关系式与目标函数分别为( )A解析:由题意可知A正确,选A.3.(2019·天津高二检测)某企业生产甲、乙两种产品均需用A,B两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为( )D (A)12万元 (B)16万元
(C)17万元 (D)18万元4.某厂拟用集装箱托运甲、乙两种货物,集装箱的体积、质量、可获利润和托运能力限制数据列在下表中,那么为了获得最大利润,甲、乙两种货物应各托运的箱数为( )A(A)4,1 (B)3,2 (C)1,4 (D)2,45.某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每台的租赁费为200元,设备乙每台的租赁费为300元,现该公司每天至少要生产A类产品50件,B类产品140件,所需租赁费最少为
元.?答案:2 300点击进入 课时作业
(1)设出未知数(当数据较多时,可以列表格来分析数据);(2)列出约束条件,确立目标函数;(3)作出可行域;(4)利用图解法求出最优解;(5)得出结论.即时训练1-1:某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨.销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨,求该企业在一个生产周期内可获得的最大利润.解:设生产甲产品x吨,生产乙产品y吨,则有关系[备用例1](1)某公司计划同时出售电子琴和洗衣机,由于两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力等)确定产品的月供应量,以使得总利润达到最大,已知对这两种产品有直接限制的因素是资金和劳动力,通过调查,得到关于两种产品的有关数据如下表:试问:怎样确定两种货的供应量,才能使总利润最大,最大利润是多少?(2)(2016·天津卷)某化肥厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料.生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示:现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.分别用x,y表示计划生产甲、乙两种肥料的车皮数.
①用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;②问分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?并求出此最大利润.题型二 求最小值的实际应用问题[例2](2019·山东菏泽检测)某公司的仓库A存有货物12 t, 仓库B存有货物8 t.现按7 t,8 t和5 t把货物分别调运给甲、乙、丙三个商店,从仓库A运货物到商店甲、乙、丙,每吨货物的运费分别为8元、6元、9元;从仓库B运货物到商店甲、乙、丙,每吨货物的运费分别为3元、4元、5元.应如何安排调运方案,才能使得从两个仓库运货物到三个商店的总运费最少?可行域如图所示.
作直线l:x-2y=0,把直线l平行移动,当直线l移至点A(0,8)时,z=x-2y+126取得最小值, zmin=0-2×8+126=110,即x=0,y=8时,总运费最少.
即仓库A运给甲、乙、丙商店的货物分别为0 t,8 t,4 t,仓库B运给甲、乙、丙商店的货物分别为7 t,0 t,1 t,此时可使得从两个仓库运货物到三个商店的总运费最少.方法技巧解答线性规划应用题应注意以下几点:
(1)在线性规划问题的应用中,常常是题中的条件较多,因此认真审题非常重要;(2)线性约束条件中有无等号要依据条件加以判断;
(3)结合实际问题,分析未知数x,y等是否有限制,如x,y为正整数、非负数等;
(4)分清线性约束条件和线性目标函数,线性约束条件一般是不等式,而线性目标函数却是一个等式.即时训练2-1:某人承揽一项业务,需做文字标牌4个,绘画标牌5个,现有两种规格的原料,甲种规格每张3 m2,可做文字标牌1个,绘画标牌2个;乙种规格每张2 m2,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张,才能使得总用料面积最小.所用原料的总面积为z=3x+2y,
作出可行域如图.
在一组平行直线3x+2y=z中,
经过可行域内的点且到原点距离最近的直线.
此直线过直线2x+y=5和直线x+2y=4的交点(2,1).
所以最优解为x=2,y=1,
所以使用甲种规格原料2张,乙种规格原料1张,可使总的用料面积最小.题型三 实际问题中的整数解问题[例3](2019·河南郑州检测)某人有一幢房子,室内面积共180 m2,拟分隔成两类房间作为游客住房.大房间每间面积为18 m2,可住游客5名,每名游客每天住宿费为 40元;小房间每间面积为15 m2,可住游客3名,每名游客每天住宿费为50元;装修大房间每间需1 000元,装修小房间每间需600元.如果他只能筹款8 000元用于装修,且游客能住满客房,他应隔出大房间和小房间各多少间,才能获得最大收益?方法技巧对于线性规划中最优整数解的问题,当解方程组得到的解不是整数解时,可用下面的方法求解:
(1)平移直线法:先在可行域内打网格,再描整点,平移直线l,最先经过或最后经过的整点坐标是整点最优解.(2)检验优值法:当可行域内整点个数较少时,也可将整点坐标逐一代入目标函数求值,经比较得出最优解.
(3)调整优值法:先求非整点最优解及最优值,再借助不定方程知识调整最优值,最后筛选出最优解.即时训练3-1:某运输公司接受了向抗洪抢险地方每天至少运送180吨支援物资的任务,该公司有8辆载重为6吨的A型卡车与4辆载重为10吨的B型卡车,有10名驾驶员,每辆卡车每天往返的次数是A型卡车为4次,B型卡车为3次.每辆卡车每天往返的成本费为A型卡车为320元,B型卡车为504元,请你为该公司调配车辆,使公司所花成本费最低.作直线l′:320x+504y=0.
作一组与l′平行的直线l:
320x+504y=t(t∈R),
由题设x,y是可行域内的整点的横、纵坐标.
在可行域内的整点中,点(8,0)使t取最小值,
即当l过点(8,0)时,t最小,
即zmin=8×320=2 560.
答:每天从公司调A型卡车8辆就能完成任务,且公司所花成本费最低.[备用例2](2019·山东烟台高二检测)某营养师要为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C.如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和
晚餐?则z在可行域的四个顶点A(9,0),B(4,3),C(2,5),D(0,8)处的值分别是
zA=2.5×9+4×0=22.5,
zB=2.5×4+4×3=22,
zC=2.5×2+4×5=25,
zD=2.5×0+4×8=32.
zB最小,
因此,应当为该儿童预订4个单位的午餐和3个单位的晚餐,就可满足
要求.题型四 易错辨析——寻找可行域内整点致误纠错:(1)本题错误的原因是①没能准确作出一组平行直线y=-x+z;②可行域内的整点寻找不准确.
(2)准确作图,充分考虑实际问题的特殊性.当图上的整点不好分辨时,应将几个有可能符合题意的整点的坐标都求出来然后逐一检验,而不能采取“四舍五入”的办法.目标函数为z=x+y,
作一组平行直线y=-x+z,
经过可行域内的点且和原点距离最大的直线必为过点B(8,0)的直线,这时x+y=8.
因为x,y均为正整数,
所以(8,0)不是最优解.
在可行域内找整点,使x+y=7.
经验证,可知点(2,5),(3,4),(4,3),(5,2),(6,1)均为最优解.
答:每根钢管截500 mm的毛坯两根,600 mm的毛坏五根,或截500 mm的毛坯三根,600 mm的毛坯四根,或截500 mm的毛坯四根,600 mm的毛坯三根,或截500 mm的毛坯五根,600 mm的毛坯两根,或截500 mm的毛坯六根,600 mm的毛坯一根最合理.学霸经验分享区(1)利用线性规划求最大值、最小值问题,主要是利润最大、效率最高、省工、省材料等问题,要将求最值的变量设为z,将z表示成其他变量的函数,求其最大值或最小值.(2)对于线性规划问题,由于题干太长,数据太多,为便于理清数据间的关系,不妨用列表法.
(3)在实际应用问题中,有些最优解往往需要整数解(比如人数、车辆数等)而直接根据约束条件得到的不一定是整数解,可以运用枚举法验证求最优整数解,或者运用平移直线求最优整数解.最优整数解有时并非只有一个,应具体情况具体分析.课堂达标解析:由题意,要运送最多的货物,先找到两类型汽车运送的总货物量,即z=6x+4y.选A.1.现有5辆载重6吨的汽车,4辆载重4吨的汽车,设需x辆载重6吨汽车和y辆载重4吨汽车,要运送最多的货物,完成这项运输任务的线性目标函数为( )
(A)z=6x+4y (B)z=5x+4y
(C)z=x+y (D)z=4x+5yA2.某服装制造商有10 m2的棉布料,10 m2的羊毛料和6 m2的丝绸料,做一条裤子需要1 m2的棉布料,2 m2的羊毛料和1 m2的丝绸料,做一条裙子需要1 m2的棉布料,1 m2的羊毛料和1 m2的丝绸料,做一条裤子的纯收益是 20元,一条裙子的纯收益是40元,为了使收益达到最大,若生产裤子x条,裙子y条,利润为z元,则生产这两种服装所满足的数学关系式与目标函数分别为( )A解析:由题意可知A正确,选A.3.(2019·天津高二检测)某企业生产甲、乙两种产品均需用A,B两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为( )D (A)12万元 (B)16万元
(C)17万元 (D)18万元4.某厂拟用集装箱托运甲、乙两种货物,集装箱的体积、质量、可获利润和托运能力限制数据列在下表中,那么为了获得最大利润,甲、乙两种货物应各托运的箱数为( )A(A)4,1 (B)3,2 (C)1,4 (D)2,45.某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每台的租赁费为200元,设备乙每台的租赁费为300元,现该公司每天至少要生产A类产品50件,B类产品140件,所需租赁费最少为
元.?答案:2 300点击进入 课时作业
