人教A版高中数学必修五 课件:3.3.2 第一课时 简单的线性规划问题 :36张PPT
文档属性
| 名称 | 人教A版高中数学必修五 课件:3.3.2 第一课时 简单的线性规划问题 :36张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 00:00:00 | ||
图片预览











文档简介
课件36张PPT。3.3.2 简单的线性规划问题
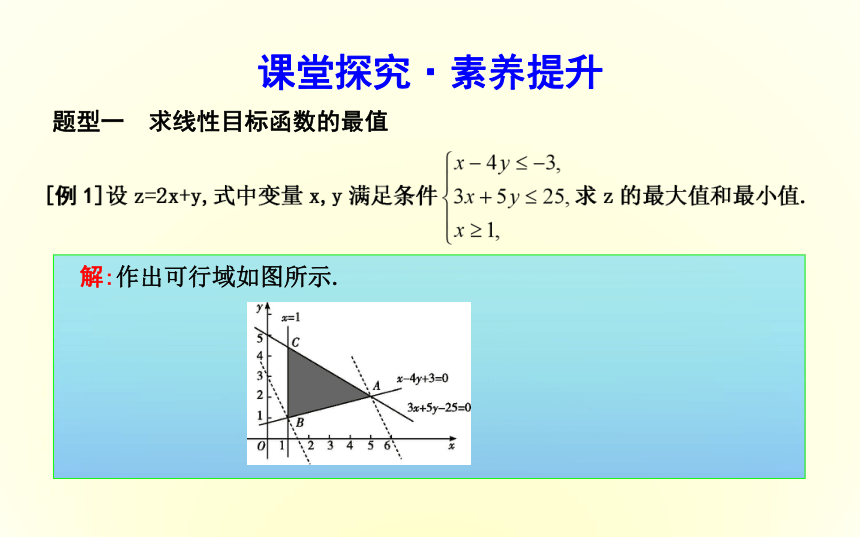
第一课时 简单的线性规划问题[目标导航]新知导学课堂探究线性规划中的基本概念新知导学·素养养成一次解集合思考1:在线性约束条件下,最优解唯一吗?答案:不一定.可能没有,可能有一个或无数个.思考2:目标函数中的z一定都是直线在y轴上的截距吗?名师点津(1)线性约束条件包括两点:一是变量x,y的不等式(或等式),二是次数为1.(2)目标函数与线性目标函数的概念不同,线性目标函数在变量x,y的次数上作了严格的限定:一次解析式,即目标函数包括线性目标函数和非线性目标函数.
(3)可行解必须使约束条件成立,而可行域是所有的可行解组成的一个集合.课堂探究·素养提升解:作出可行域如图所示.题型一 求线性目标函数的最值方法技巧(1)一般地,对目标函数z=ax+by,若b>0,则纵截距与z同号,因此,纵截距最大时,z也最大;若b<0,则纵截距与z异号,因此,纵截距最大时,z反而最小.(2)解二元线性规划问题的一般步骤
①画:在直角坐标平面上画出可行域和直线ax+by=0(目标函数为z=
ax+by);
②移:平行移动直线ax+by=0,确定使z=ax+by取得最大值或最小值的点;
③求:求出取得最大值或最小值的点的坐标(解方程组)及最大值和最小值;
④答:给出正确答案.答案:(1)3解析:(2) 画出可行域如图.
可行域为△ABC的内部及其边界.
设x+y=t,
则y=-x+t,t的几何意义为直线y=-x+t在y轴上的截距,当直线通过点A,B时,t取得最小值与最大值,可求得A,B两点的坐标分别为(1,0)和(2,1),所以1≤t≤3,即x+y的取值范围是[1,3].答案:(2)[1,3]题型二 求非线性目标函数的最值(1)求u=x2+y2的最大值与最小值;规范解答:画出满足条件的可行域,如图中阴影部分所示.(1)u=x2+y2(除原点)表示一组同心圆(圆心为原点O),由图可知,当(x,y)在可行域内取值时,当且仅当圆O过C点时,u最大,取(0,0)时,u最小.又C(3,8),所以umax=73,umin=0.…………4分(3)求z=|2x+y+4|的最大值与最小值.方法技巧非线性目标函数的最值的求解策略
(1)z=(x-a)2+(y-b)2型的目标函数可转化为点(x,y)与点(a,b)距离的平方.特别地,z=x2+y2型的目标函数表示可行域内的点到原点的距离的平方.(2)一元二次方程x2+ax+2b=0有两个根,一个根在区间[0,1]内,另一个根在区间[1,2]内.
①求点(a,b)对应的区域的面积;③求(a-1)2+(b-2)2的值域.解:③由②易知(a-1)2+(b-2)2=|PD|2,
|CD|2≤|PD|2≤|AD|2,
因为|AD|2=17,|CD|2=8,
所以8≤(a-1)2+(b-2)2≤17,
所以(a-1)2+(b-2)2的取值范围是[8,17].题型三 线性规划中的参数问题答案:(1,+∞)一题多变:在本例条件下,若目标函数z=ax+y(a>0)取得最大值的点有无数个,求a的值.解:结合本例中图形,若z=ax+y(a>0)取得最大值的点有无数个,则必有直线z=ax+y与x+y=4重合,即-a=-1,此时a=1.方法技巧根据目标函数的最值求参数的解题思路
采用数形结合,先画出可行域,根据目标函数表示的意义,画出目标函数等于最值的直线,它与相应直线的交点就是最优解,再将所求出的最优解代入含有参数的约束条件,即可求出参数的值或范围.(A)-2 (B)-1 (C)1 (D)2学霸经验分享区(1)用图解法求线性目标函数的最值时,由于关键步骤基本上是在图上完成的,所以作图一定要准确;其次要弄清z的含义,z总是与直线的纵截距有关;平移直线时,要注意线性目标函数的斜率与可行域中边界直线的斜率进行比较,以确定最优解.(2)解决非线性目标函数问题时,要首先考虑目标函数的几何意义,再结合图形解决.课堂达标解析:把目标函数变形为y=2x-z,由此可见,z是该直线在y轴上的截距的相反数.故选C.1.目标函数z=2x-y,将其看成直线方程时,z的意义是( )
(A)该直线在坐标轴上的距离
(B)该直线在y轴上的截距
(C)该直线在y轴上的截距的相反数
(D)该直线在x轴上的截距C(A)-7 (B)-6 (C)-5 (D)-3B3. 已知平面区域如图所示,z=mx+y(m>0)在平面区域内取得最大值的最优解有无数多个,则m的值为( )B点击进入 课时作业
第一课时 简单的线性规划问题[目标导航]新知导学课堂探究线性规划中的基本概念新知导学·素养养成一次解集合思考1:在线性约束条件下,最优解唯一吗?答案:不一定.可能没有,可能有一个或无数个.思考2:目标函数中的z一定都是直线在y轴上的截距吗?名师点津(1)线性约束条件包括两点:一是变量x,y的不等式(或等式),二是次数为1.(2)目标函数与线性目标函数的概念不同,线性目标函数在变量x,y的次数上作了严格的限定:一次解析式,即目标函数包括线性目标函数和非线性目标函数.
(3)可行解必须使约束条件成立,而可行域是所有的可行解组成的一个集合.课堂探究·素养提升解:作出可行域如图所示.题型一 求线性目标函数的最值方法技巧(1)一般地,对目标函数z=ax+by,若b>0,则纵截距与z同号,因此,纵截距最大时,z也最大;若b<0,则纵截距与z异号,因此,纵截距最大时,z反而最小.(2)解二元线性规划问题的一般步骤
①画:在直角坐标平面上画出可行域和直线ax+by=0(目标函数为z=
ax+by);
②移:平行移动直线ax+by=0,确定使z=ax+by取得最大值或最小值的点;
③求:求出取得最大值或最小值的点的坐标(解方程组)及最大值和最小值;
④答:给出正确答案.答案:(1)3解析:(2) 画出可行域如图.
可行域为△ABC的内部及其边界.
设x+y=t,
则y=-x+t,t的几何意义为直线y=-x+t在y轴上的截距,当直线通过点A,B时,t取得最小值与最大值,可求得A,B两点的坐标分别为(1,0)和(2,1),所以1≤t≤3,即x+y的取值范围是[1,3].答案:(2)[1,3]题型二 求非线性目标函数的最值(1)求u=x2+y2的最大值与最小值;规范解答:画出满足条件的可行域,如图中阴影部分所示.(1)u=x2+y2(除原点)表示一组同心圆(圆心为原点O),由图可知,当(x,y)在可行域内取值时,当且仅当圆O过C点时,u最大,取(0,0)时,u最小.又C(3,8),所以umax=73,umin=0.…………4分(3)求z=|2x+y+4|的最大值与最小值.方法技巧非线性目标函数的最值的求解策略
(1)z=(x-a)2+(y-b)2型的目标函数可转化为点(x,y)与点(a,b)距离的平方.特别地,z=x2+y2型的目标函数表示可行域内的点到原点的距离的平方.(2)一元二次方程x2+ax+2b=0有两个根,一个根在区间[0,1]内,另一个根在区间[1,2]内.
①求点(a,b)对应的区域的面积;③求(a-1)2+(b-2)2的值域.解:③由②易知(a-1)2+(b-2)2=|PD|2,
|CD|2≤|PD|2≤|AD|2,
因为|AD|2=17,|CD|2=8,
所以8≤(a-1)2+(b-2)2≤17,
所以(a-1)2+(b-2)2的取值范围是[8,17].题型三 线性规划中的参数问题答案:(1,+∞)一题多变:在本例条件下,若目标函数z=ax+y(a>0)取得最大值的点有无数个,求a的值.解:结合本例中图形,若z=ax+y(a>0)取得最大值的点有无数个,则必有直线z=ax+y与x+y=4重合,即-a=-1,此时a=1.方法技巧根据目标函数的最值求参数的解题思路
采用数形结合,先画出可行域,根据目标函数表示的意义,画出目标函数等于最值的直线,它与相应直线的交点就是最优解,再将所求出的最优解代入含有参数的约束条件,即可求出参数的值或范围.(A)-2 (B)-1 (C)1 (D)2学霸经验分享区(1)用图解法求线性目标函数的最值时,由于关键步骤基本上是在图上完成的,所以作图一定要准确;其次要弄清z的含义,z总是与直线的纵截距有关;平移直线时,要注意线性目标函数的斜率与可行域中边界直线的斜率进行比较,以确定最优解.(2)解决非线性目标函数问题时,要首先考虑目标函数的几何意义,再结合图形解决.课堂达标解析:把目标函数变形为y=2x-z,由此可见,z是该直线在y轴上的截距的相反数.故选C.1.目标函数z=2x-y,将其看成直线方程时,z的意义是( )
(A)该直线在坐标轴上的距离
(B)该直线在y轴上的截距
(C)该直线在y轴上的截距的相反数
(D)该直线在x轴上的截距C(A)-7 (B)-6 (C)-5 (D)-3B3. 已知平面区域如图所示,z=mx+y(m>0)在平面区域内取得最大值的最优解有无数多个,则m的值为( )B点击进入 课时作业
