人教A版高中数学必修五 课件:第3章末总结 :26张PPT
文档属性
| 名称 | 人教A版高中数学必修五 课件:第3章末总结 :26张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 22:19:37 | ||
图片预览








文档简介
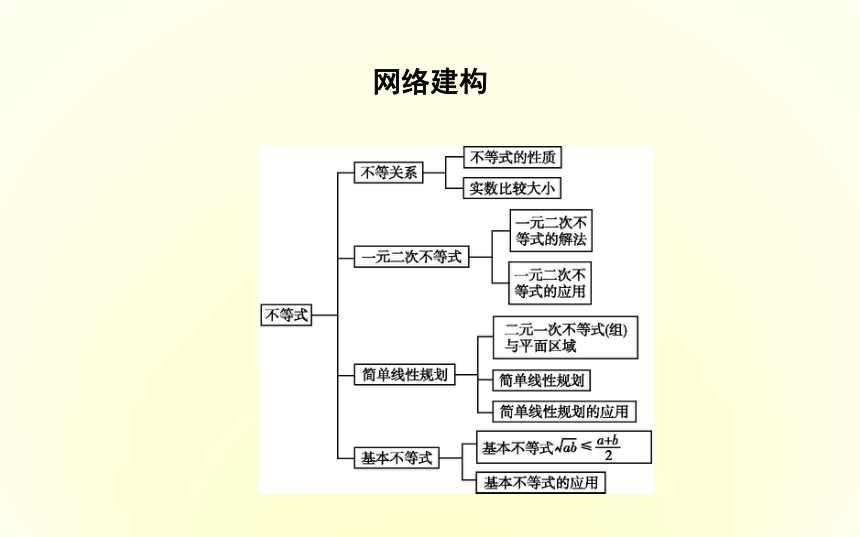
课件26张PPT。章末总结网络建构知识辨析判断下列说法是否正确.(请在括号中填“√”或“×”)
1.某变量y不超过a可表示为“y≥a”.( )×2.设a=3x2-x+1,b=2x2+x,x∈R,则a≥b.( )√×4.ax2+bx+c>0是一元二次不等式.( )×5.点(2,0)不在3x+2y<6表示的平面区域内.( )√×7.若x>0,y>0,且x+y=2,则2xy的最大值为1.( )××题型探究·素养提升题型一 不等式的性质及应用[典例1]如果a,b,c满足c(A)ab>ac (B)c(b-a)>0
(C)cb20的解集为{x|x<1或x>b}.
(1)求a,b;(2)解不等式ax2-(ac+b)x+bc<0.规律总结解含参数的不等式,一般分类标准有:
(1)按二次项系数等于0与不等于0分类;(2)二次项系数不为零时,按判别式Δ进行分类;
(3)当Δ>0时,按根的大小进行分类.题型三 简单的线性规划答案:9(2)某企业生产A,B两种产品,生产每吨产品所需的劳动力、煤和电耗如下表:已知生产每吨A产品的利润是7万元,生产每吨B产品的利润是12万元,现因条件限制,该企业仅有劳动力300个,煤360吨,并且供电局只能供电200千瓦,试问该企业生产A,B两种产品各多少吨,才能获得最大利润?规律总结(1)求目标函数最值的一般步骤为一画、二移、三求.其关键是准确作出可行域,理解目标函数的意义.(2)在约束条件是线性的情况下,线性目标函数只有在可行域的顶点或者边界上取得最值,在解答选择题或者填空题时也可以根据可行域的顶点直接进行检验.题型四 利用基本不等式求最值[典例4](1)已知0(1)坐标法
把几何图形放在适当的坐标系中,则有关点与向量就可以用坐标表示,这样就能进行相应的代数运算和向量运算,从而使问题得到解决.
(2)基向量法
适当选取一组基底,沟通向量之间的联系,利用向量间的关系构造关于未知量的方程进行求解.答案:-2 85.(2018·北京卷)若x,y满足x+1≤y≤2x,则2y-x的最小值是
.?答案:3点击进入 检测试题
1.某变量y不超过a可表示为“y≥a”.( )×2.设a=3x2-x+1,b=2x2+x,x∈R,则a≥b.( )√×4.ax2+bx+c>0是一元二次不等式.( )×5.点(2,0)不在3x+2y<6表示的平面区域内.( )√×7.若x>0,y>0,且x+y=2,则2xy的最大值为1.( )××题型探究·素养提升题型一 不等式的性质及应用[典例1]如果a,b,c满足c
(C)cb2
(1)求a,b;(2)解不等式ax2-(ac+b)x+bc<0.规律总结解含参数的不等式,一般分类标准有:
(1)按二次项系数等于0与不等于0分类;(2)二次项系数不为零时,按判别式Δ进行分类;
(3)当Δ>0时,按根的大小进行分类.题型三 简单的线性规划答案:9(2)某企业生产A,B两种产品,生产每吨产品所需的劳动力、煤和电耗如下表:已知生产每吨A产品的利润是7万元,生产每吨B产品的利润是12万元,现因条件限制,该企业仅有劳动力300个,煤360吨,并且供电局只能供电200千瓦,试问该企业生产A,B两种产品各多少吨,才能获得最大利润?规律总结(1)求目标函数最值的一般步骤为一画、二移、三求.其关键是准确作出可行域,理解目标函数的意义.(2)在约束条件是线性的情况下,线性目标函数只有在可行域的顶点或者边界上取得最值,在解答选择题或者填空题时也可以根据可行域的顶点直接进行检验.题型四 利用基本不等式求最值[典例4](1)已知0
把几何图形放在适当的坐标系中,则有关点与向量就可以用坐标表示,这样就能进行相应的代数运算和向量运算,从而使问题得到解决.
(2)基向量法
适当选取一组基底,沟通向量之间的联系,利用向量间的关系构造关于未知量的方程进行求解.答案:-2 85.(2018·北京卷)若x,y满足x+1≤y≤2x,则2y-x的最小值是
.?答案:3点击进入 检测试题
