人教版六上第8单元《数学广角-数与形》同步练习(含答案及解析)
文档属性
| 名称 | 人教版六上第8单元《数学广角-数与形》同步练习(含答案及解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 125.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-27 00:00:00 | ||
图片预览


文档简介
第8单元《数与形》同步练习
一、单选题。
1、按如下规律摆放三角形:
则第(5)堆三角形的个数为( )
A、14 B、15 C、16 D、17
2、按如图点阵中的规律继续画,第10个点阵应画(? )个点.
A.?90??B.?110??C.?132 D、136
3、根据 , ,那么
A、 B、 C、 D、
4、3×7=21,33×67=2211,333×667=222111,那么3333×6667=( )
A、222111 B、22221111 C、2221111 D、22221111
5、观察找规律:
用同样长的小棒摆第10个图形需要( )根小棒.
A、20 B、21 C、25 D、30
6、按如图用小棒摆正六边形,摆第51个正六边形需要________根小棒.
A、240 B、250 C、256 D、258
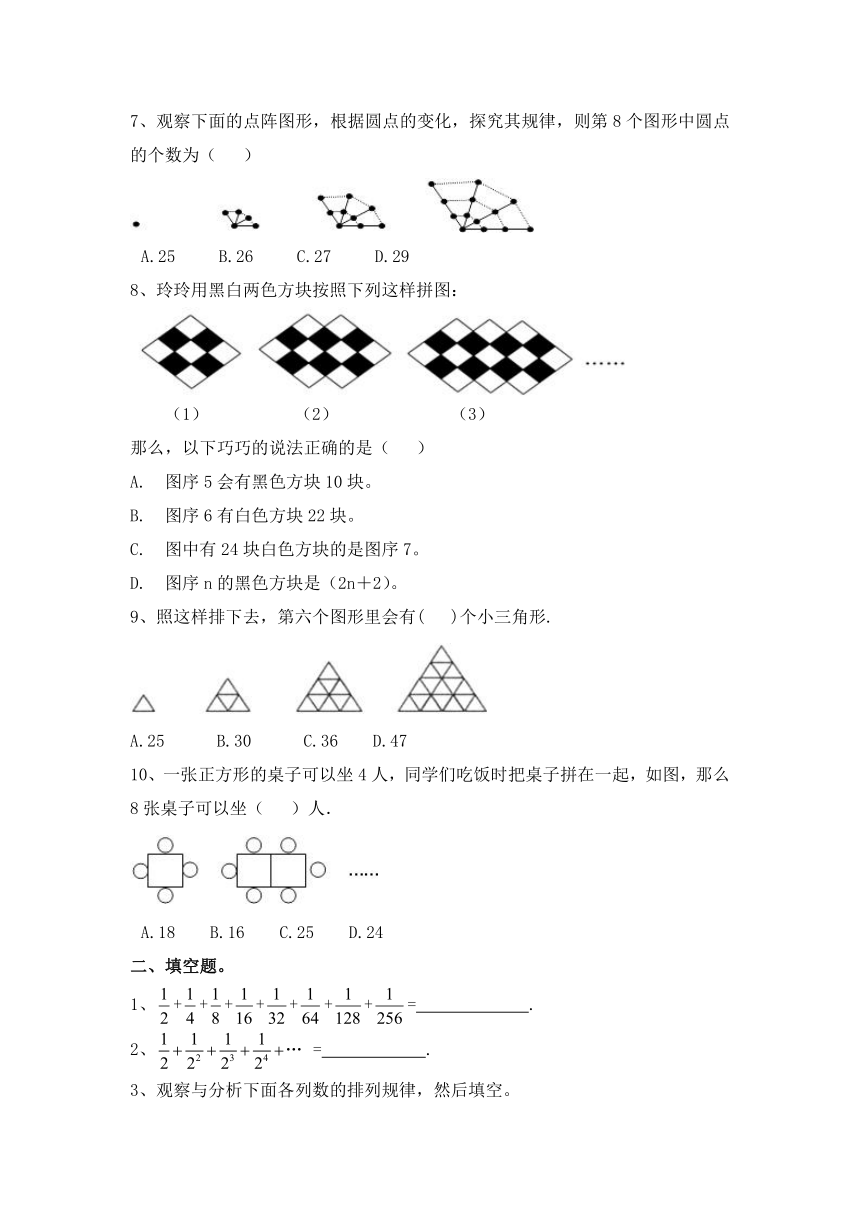
7、观察下面的点阵图形,根据圆点的变化,探究其规律,则第8个图形中圆点的个数为(? )
A.25? ?B.26? ?C.27 ?D.29
8、玲玲用黑白两色方块按照下列这样拼图:
(1) (2) (3)
那么,以下巧巧的说法正确的是( ?)
A.?图序5会有黑色方块10块。??????
B.?图序6有白色方块22块。
C.?图中有24块白色方块的是图序7。?????
D.?图序n的黑色方块是(2n+2)。
9、照这样排下去,第六个图形里会有(? )个小三角形.
A.25???B.30???C.36??D.47
10、一张正方形的桌子可以坐4人,同学们吃饭时把桌子拼在一起,如图,那么8张桌子可以坐(? )人.
A.18??B.16??C.25? D.24
二、填空题。
1、+++++++= .
2、 = .
3、观察与分析下面各列数的排列规律,然后填空。
(1)5,9,13,17, , .
(2)4,5,7,11,19, , .
(3)4,9,19,34,54, , .
(4) 45,1,43,3,41,5 , ,37,9。
4、王翔按照一定的规律写数:1、+2、﹣3、4、+5、﹣6、7、+8、﹣9、…,当写完第50个数时,他停了下来.他写的数中一共有_____个正数,_____个负数.
三、解答题。
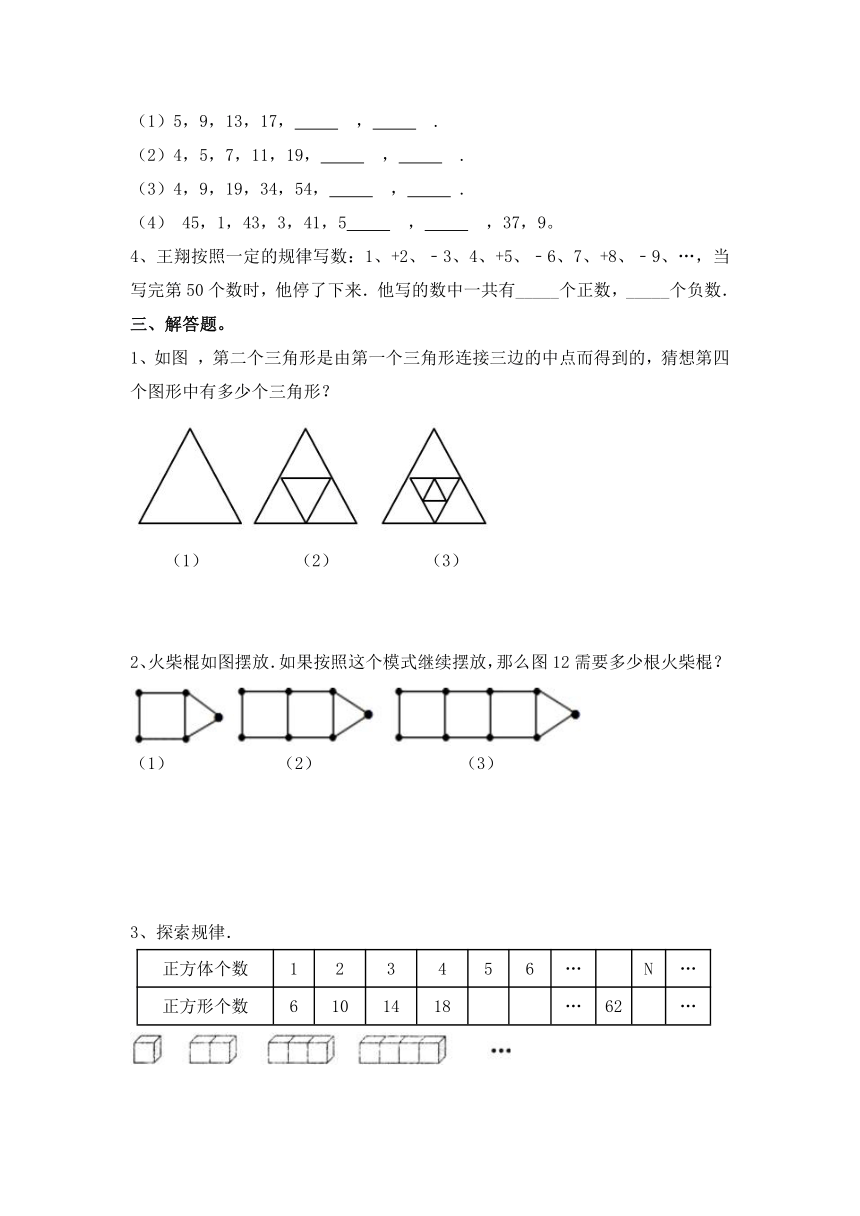
1、如图 ,第二个三角形是由第一个三角形连接三边的中点而得到的,猜想第四个图形中有多少个三角形?
(1) (2) (3)
2、火柴棍如图摆放.如果按照这个模式继续摆放,那么图12需要多少根火柴棍?
(1) (2) (3)
3、探索规律.
正方体个数 1 2 3 4 5 6 … N …
正方形个数 6 10 14 18 … 62 …
四、拓展提升。
1、(a+b)?=a?+2ab+b?你能画图来解释这一公式吗?(提示:利用正方形的面积公式来推导)
2、古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.请写出第5个图形的算式。
4=1+3 9=3+6 16=6+10
参考答案
一、单选题。
1、
【答案】D
【解析】根据题干中的图形的个数可以得出:第一个图形有2+1×3个三角形,第二个图形有2+2×3个三角形,第三个有2+3×3个三角形,第5堆有2+5×3个三角形.
2、
【答案】B
【解析】根据题意可知,当n等于10时,点阵图横排是10个点,竖排是11个点,然后列乘法算式计算即可。当n=10时,n2+n=10×10+10=110,则第10个点阵应画110个点.
3、
【答案】C
【解析】根据 , ,得出规律:分子是1,分母是两个相邻自然数的分数相减,差的分子仍然是1,分母是这两个自然数的积;因此得解.认真观察,找出规律是解决此题的关键.
4
【答案】B
【解析】因为3×7=21,33×67=2211,333×667=222111,发现乘积中2的个数及其1的个数都与因数中3的个数相同,据此解答即可.解答本题的关键是:根据已知前三道题的规律进而总结出:乘积中2的个数及其1的个数都与因数中3的个数相同.
5、
【答案】B
【解析】1个三角形所需小棒的根数=3,2个三角形所需小棒的根数=3+2,
3个三角形所需小棒的根数=3+2×2,…n个三角形所需小棒的根数=3+2×(n﹣1)=2n+1,当n=10时,2n+1=2×10+1=21(根).
6、
【答案】C
【解析】当n=1时,需要小棒1×5+1=6(根),当n=2时,需要小棒2×5+1=11
当n=3时,需要小棒3×5+1=16(根),
当n=4时,需要小棒数:4×5+1=21(根)
当n=51时,需要小棒数:51×5+1=256(根)
7、
【答案】D
【解析】根据前三个图形中圆点的个数与图形的个数判断规律:图形中圆点的个数=图形个数×4-3,由此根据规律计算即可.
8、
【答案】D
【解析】A、图序5黑色方块的个数:5×2+2=12(块),此选项错误;
B、图序6白色方块的个数:6×3+2=20(块),此选项错误;
C、图序7白色方块的个数:7×3+2=23(块),此选项错误;
D、图序n黑色方块的个数:n×2+2=2n+2,此选项正确.
9、
【答案】C
【解析】第一个图形:1×1=1(个),第二个图形:2×2=4(个)……,规律:小三角形的个数=图形个数×图形个数,根据这个规律计算小三角形的个数即可.
10、
【答案】A
【解析】第一张桌子可以坐4人,; 拼2张桌子可以坐4+2×1=6人;拼3张桌子可以坐4+2×2=8人;故n张桌子拼在一起可以坐4+2(n﹣1)=2n+2,当n=8时,2n+2=2×8+2=18(人).
二、填空题。
1、
【答案】
2、
【答案】1
3、
【答案】(1)21,25 (2)35,67 (3)79,109 (4)39,7
4、
【答案】34,16
【解析】根据题意,可从头将数列中的数每三个数分为一组,每组中前两个数为正数,后一个数为负数.50÷3=16…2.最后余两个为正数,所以共有正数:2×16+2=34(个);共有负数:16个.
三、解答题。
1、
【答案】13个
【解析】从第2个图形开始,后一个图形会比前一个图形增加4个三角形,所以第4个图形有1+4+4+4=13(个)三角形。
2、
【答案】D
【解析】图形①需要6根火柴棍,可以写成3×2;
图形②需要9根火柴棍,可以写成3×3;
图形③需要12根火柴棍,可以写成3×4,…
则图形n需要3×(n+1)=3n+3根火柴棍,
当n=12时,需要火柴棍:3×12+3=39(根).
3、
【答案】
正方体 个数 1 2 3 4 5 6 … 15 N …
正方形 个数 6 10 14 18 22 26 … 62 6+(N﹣1)×4 …
【解析】通过分析可知:每增加一个正方体,正方形的个数增加4个,10=6+4,14=6+2×4,18=6+3×4,所以N个正方体的正方形的个数是6+(N﹣1)×4,据此解答即可.
四、拓展提升。
【解析】如图:
左边的面积=(a+b)?,右边的面积=a?+2ab+b?,所以(a+b)?=a?+2ab+b?
2、
【答案】36=15+21
【解析】题目中“三角形数”的规律为1、3、6、10、15、21…“正方形数”的规律为1、4、9、16、25…,根据题目已知条件:从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.可得出最后结果 .
一、单选题。
1、按如下规律摆放三角形:
则第(5)堆三角形的个数为( )
A、14 B、15 C、16 D、17
2、按如图点阵中的规律继续画,第10个点阵应画(? )个点.
A.?90??B.?110??C.?132 D、136
3、根据 , ,那么
A、 B、 C、 D、
4、3×7=21,33×67=2211,333×667=222111,那么3333×6667=( )
A、222111 B、22221111 C、2221111 D、22221111
5、观察找规律:
用同样长的小棒摆第10个图形需要( )根小棒.
A、20 B、21 C、25 D、30
6、按如图用小棒摆正六边形,摆第51个正六边形需要________根小棒.
A、240 B、250 C、256 D、258
7、观察下面的点阵图形,根据圆点的变化,探究其规律,则第8个图形中圆点的个数为(? )
A.25? ?B.26? ?C.27 ?D.29
8、玲玲用黑白两色方块按照下列这样拼图:
(1) (2) (3)
那么,以下巧巧的说法正确的是( ?)
A.?图序5会有黑色方块10块。??????
B.?图序6有白色方块22块。
C.?图中有24块白色方块的是图序7。?????
D.?图序n的黑色方块是(2n+2)。
9、照这样排下去,第六个图形里会有(? )个小三角形.
A.25???B.30???C.36??D.47
10、一张正方形的桌子可以坐4人,同学们吃饭时把桌子拼在一起,如图,那么8张桌子可以坐(? )人.
A.18??B.16??C.25? D.24
二、填空题。
1、+++++++= .
2、 = .
3、观察与分析下面各列数的排列规律,然后填空。
(1)5,9,13,17, , .
(2)4,5,7,11,19, , .
(3)4,9,19,34,54, , .
(4) 45,1,43,3,41,5 , ,37,9。
4、王翔按照一定的规律写数:1、+2、﹣3、4、+5、﹣6、7、+8、﹣9、…,当写完第50个数时,他停了下来.他写的数中一共有_____个正数,_____个负数.
三、解答题。
1、如图 ,第二个三角形是由第一个三角形连接三边的中点而得到的,猜想第四个图形中有多少个三角形?
(1) (2) (3)
2、火柴棍如图摆放.如果按照这个模式继续摆放,那么图12需要多少根火柴棍?
(1) (2) (3)
3、探索规律.
正方体个数 1 2 3 4 5 6 … N …
正方形个数 6 10 14 18 … 62 …
四、拓展提升。
1、(a+b)?=a?+2ab+b?你能画图来解释这一公式吗?(提示:利用正方形的面积公式来推导)
2、古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.请写出第5个图形的算式。
4=1+3 9=3+6 16=6+10
参考答案
一、单选题。
1、
【答案】D
【解析】根据题干中的图形的个数可以得出:第一个图形有2+1×3个三角形,第二个图形有2+2×3个三角形,第三个有2+3×3个三角形,第5堆有2+5×3个三角形.
2、
【答案】B
【解析】根据题意可知,当n等于10时,点阵图横排是10个点,竖排是11个点,然后列乘法算式计算即可。当n=10时,n2+n=10×10+10=110,则第10个点阵应画110个点.
3、
【答案】C
【解析】根据 , ,得出规律:分子是1,分母是两个相邻自然数的分数相减,差的分子仍然是1,分母是这两个自然数的积;因此得解.认真观察,找出规律是解决此题的关键.
4
【答案】B
【解析】因为3×7=21,33×67=2211,333×667=222111,发现乘积中2的个数及其1的个数都与因数中3的个数相同,据此解答即可.解答本题的关键是:根据已知前三道题的规律进而总结出:乘积中2的个数及其1的个数都与因数中3的个数相同.
5、
【答案】B
【解析】1个三角形所需小棒的根数=3,2个三角形所需小棒的根数=3+2,
3个三角形所需小棒的根数=3+2×2,…n个三角形所需小棒的根数=3+2×(n﹣1)=2n+1,当n=10时,2n+1=2×10+1=21(根).
6、
【答案】C
【解析】当n=1时,需要小棒1×5+1=6(根),当n=2时,需要小棒2×5+1=11
当n=3时,需要小棒3×5+1=16(根),
当n=4时,需要小棒数:4×5+1=21(根)
当n=51时,需要小棒数:51×5+1=256(根)
7、
【答案】D
【解析】根据前三个图形中圆点的个数与图形的个数判断规律:图形中圆点的个数=图形个数×4-3,由此根据规律计算即可.
8、
【答案】D
【解析】A、图序5黑色方块的个数:5×2+2=12(块),此选项错误;
B、图序6白色方块的个数:6×3+2=20(块),此选项错误;
C、图序7白色方块的个数:7×3+2=23(块),此选项错误;
D、图序n黑色方块的个数:n×2+2=2n+2,此选项正确.
9、
【答案】C
【解析】第一个图形:1×1=1(个),第二个图形:2×2=4(个)……,规律:小三角形的个数=图形个数×图形个数,根据这个规律计算小三角形的个数即可.
10、
【答案】A
【解析】第一张桌子可以坐4人,; 拼2张桌子可以坐4+2×1=6人;拼3张桌子可以坐4+2×2=8人;故n张桌子拼在一起可以坐4+2(n﹣1)=2n+2,当n=8时,2n+2=2×8+2=18(人).
二、填空题。
1、
【答案】
2、
【答案】1
3、
【答案】(1)21,25 (2)35,67 (3)79,109 (4)39,7
4、
【答案】34,16
【解析】根据题意,可从头将数列中的数每三个数分为一组,每组中前两个数为正数,后一个数为负数.50÷3=16…2.最后余两个为正数,所以共有正数:2×16+2=34(个);共有负数:16个.
三、解答题。
1、
【答案】13个
【解析】从第2个图形开始,后一个图形会比前一个图形增加4个三角形,所以第4个图形有1+4+4+4=13(个)三角形。
2、
【答案】D
【解析】图形①需要6根火柴棍,可以写成3×2;
图形②需要9根火柴棍,可以写成3×3;
图形③需要12根火柴棍,可以写成3×4,…
则图形n需要3×(n+1)=3n+3根火柴棍,
当n=12时,需要火柴棍:3×12+3=39(根).
3、
【答案】
正方体 个数 1 2 3 4 5 6 … 15 N …
正方形 个数 6 10 14 18 22 26 … 62 6+(N﹣1)×4 …
【解析】通过分析可知:每增加一个正方体,正方形的个数增加4个,10=6+4,14=6+2×4,18=6+3×4,所以N个正方体的正方形的个数是6+(N﹣1)×4,据此解答即可.
四、拓展提升。
【解析】如图:
左边的面积=(a+b)?,右边的面积=a?+2ab+b?,所以(a+b)?=a?+2ab+b?
2、
【答案】36=15+21
【解析】题目中“三角形数”的规律为1、3、6、10、15、21…“正方形数”的规律为1、4、9、16、25…,根据题目已知条件:从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.可得出最后结果 .
