青岛版九年级数学下册5.5确定二次函数的表达式课件(18张ppt)
文档属性
| 名称 | 青岛版九年级数学下册5.5确定二次函数的表达式课件(18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 979.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 09:44:24 | ||
图片预览





文档简介
(共18张PPT)
5.5确定二次函数
的表达式
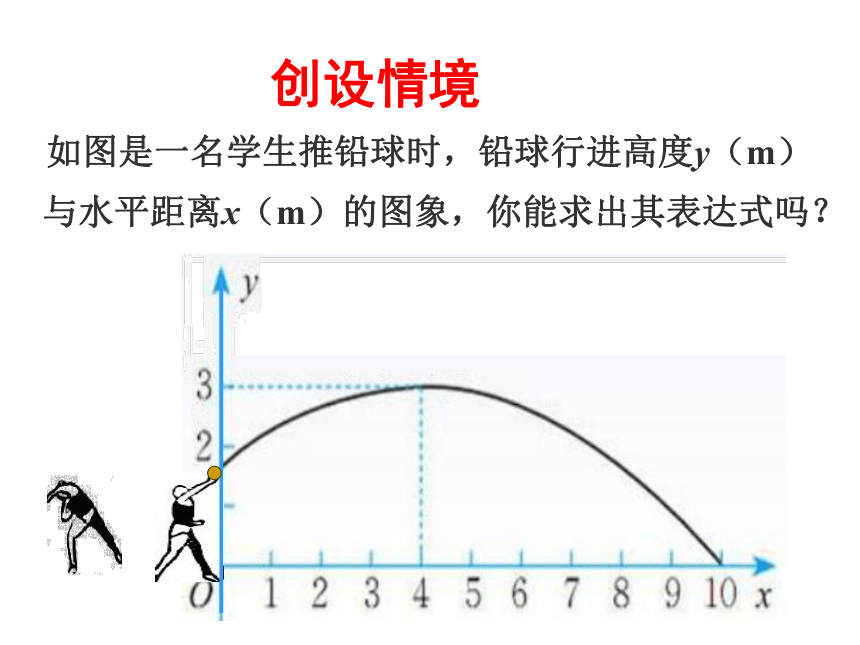
如图是一名学生推铅球时,铅球行进高度y(m)与水平距离x(m)的图象,你能求出其表达式吗?
创设情境
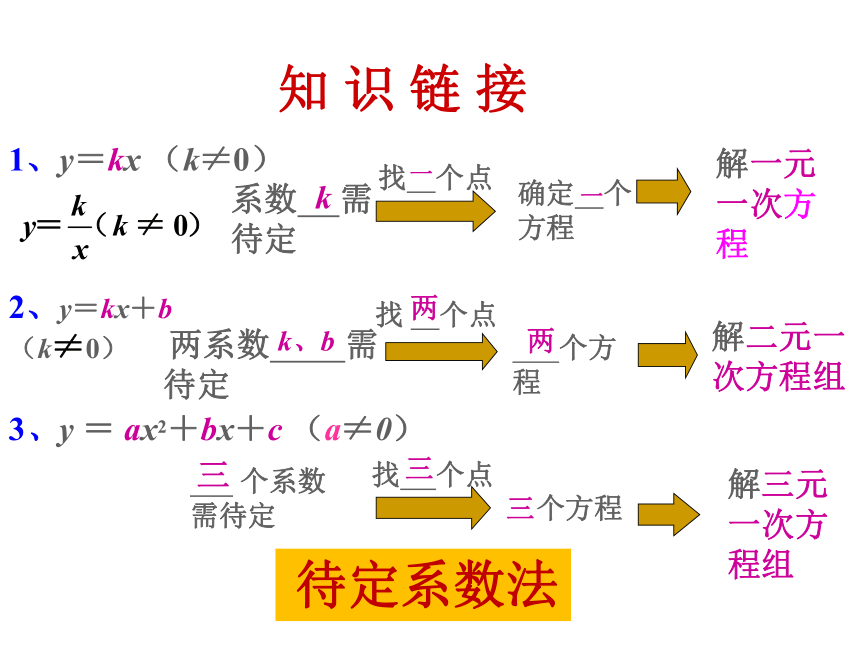
1、y=kx (k≠0)
2、y=kx+b(k≠0)
系数 需待定
找 个点
确定 个
方程
解一元一次方程
两系数 需待定
找 个点
个方程
解二元一次方程组
3、y = ax2+bx+c (a≠0)
个系数需待定
找 个点
个方程
解三元一次方程组
待定系数法
知 识 链 接
k
一
一
两
三
三
三
k、b
两
学习目标
1、会利用( 一般式 )确定二次函数的表达式
2、会选择( 顶点式 )的方法求二次函数表达式
数学知识我先知
自学课本例2
自学指导:
1、怎样求二次函数解析式?
2、这种方法的步骤:
3、你认为这种方法的难点是?
若二次函数图象过A(1,0),B(0,2), C(-1,2)三点,求此函数的解析式。
解:设二次函数表达式为:y=ax2+bx+c
∵? 图象经过点
∴? ?? ? ? ???
解得?
∴? 函数的解析式为:
最合适的方法是:步骤:
实战演练
乘胜追击
自学例1
仔细观察例1与例2有什么不同?
你认为这种方法的难点在哪里?
测一测
已知顶点坐标,如何设二次函数表达式?
(1)顶点(1,2),设y=a(x ___)2_____
(2)顶点(-1,2),设y=a(x ___)2_____
(3)顶点(1,-2),设y=a(x ___)2_____
(4)顶点(-1,-2),设y=a(x ___)2_____
(5)顶点(h,k),设y=a(x ___)2_____
-1
+2
+1
+2
-1
+1
-2
-2
-h
+k
比比谁最牛!
已知抛物线的顶点坐标是(-1,-2),且图象还过点(1,10),求这个二次函数的表达式。
解法1:(利用一般式)------太麻烦
解法2:(利用顶点式)------合适的解法
拓展提升
已知一个二次函数的图象经过点(4,-3),并且当x=3时有最大值4,试确定这个二次函数的解析式。
1、抛物线的形状、开口方向都与抛物线y=-x2相同顶点在(1,-2),则抛物线的解析式为________________________________.
2、已知二次函数的对称轴是直线x=1,图象上最低点 P的纵坐标式-8,图象还过点(-2,10),设函数表达式____________________________。
3、已知二次函数图像经过点A(1,-2),B(-1,6),C,2,-6),设二次函数表达式_____________。
变式训练
学以致用
如图是一名学生推铅球时,铅球行进高度y(m)与水平距离x(m)的图象,你能求出其表达式吗?
解:由图像知,抛物线的顶点为(4,3),过点(10,0)可设抛物线解析式为
把(10,0)代入上式,得
在确定二次函数的表达式时
(1)若已知图像上三个非特殊点,常设一般式 ;
(2)若已知二次函数顶点坐标或对称轴,或最大值,最小值,常设顶点式 较为简便;
温馨提示
学贵有思
1、本节课你学到了……
2、你还有什么困惑?
选择最优解法,求下列二次函数表达式:
1、已知抛物线的图象经过点(1,1) 、(﹣1,﹣1) 、(0,﹣2) ,设抛物线解析式为___________________
2、已知抛物线的顶点坐标(﹣2,3) ,且经过点(﹣1,0) ,设抛物线解析式为____________________
3、已知二次函数有最大值6,对称轴是直线x=2,设抛物线解析式为____________________
过关一
y=ax2+bx+c(a≠0)
y=a(x+2)2+3(a≠0)
y=a(x-2)2+6(a≠0)
二次函数y=ax2+bx+c的图象过点A(1,0),B(2,0)两点,且经过点(3,4),求这个二次函数的解析式。
课后延伸
谢谢!
温故知新
1.二次函数表达式的一般形式是________________,
顶点坐标是__________________。
二次函数表达式的顶点式是______________。
3.
y=ax2+bx+c(a≠0)
y=a(x-h)2+k
5.5确定二次函数
的表达式
如图是一名学生推铅球时,铅球行进高度y(m)与水平距离x(m)的图象,你能求出其表达式吗?
创设情境
1、y=kx (k≠0)
2、y=kx+b(k≠0)
系数 需待定
找 个点
确定 个
方程
解一元一次方程
两系数 需待定
找 个点
个方程
解二元一次方程组
3、y = ax2+bx+c (a≠0)
个系数需待定
找 个点
个方程
解三元一次方程组
待定系数法
知 识 链 接
k
一
一
两
三
三
三
k、b
两
学习目标
1、会利用( 一般式 )确定二次函数的表达式
2、会选择( 顶点式 )的方法求二次函数表达式
数学知识我先知
自学课本例2
自学指导:
1、怎样求二次函数解析式?
2、这种方法的步骤:
3、你认为这种方法的难点是?
若二次函数图象过A(1,0),B(0,2), C(-1,2)三点,求此函数的解析式。
解:设二次函数表达式为:y=ax2+bx+c
∵? 图象经过点
∴? ?? ? ? ???
解得?
∴? 函数的解析式为:
最合适的方法是:步骤:
实战演练
乘胜追击
自学例1
仔细观察例1与例2有什么不同?
你认为这种方法的难点在哪里?
测一测
已知顶点坐标,如何设二次函数表达式?
(1)顶点(1,2),设y=a(x ___)2_____
(2)顶点(-1,2),设y=a(x ___)2_____
(3)顶点(1,-2),设y=a(x ___)2_____
(4)顶点(-1,-2),设y=a(x ___)2_____
(5)顶点(h,k),设y=a(x ___)2_____
-1
+2
+1
+2
-1
+1
-2
-2
-h
+k
比比谁最牛!
已知抛物线的顶点坐标是(-1,-2),且图象还过点(1,10),求这个二次函数的表达式。
解法1:(利用一般式)------太麻烦
解法2:(利用顶点式)------合适的解法
拓展提升
已知一个二次函数的图象经过点(4,-3),并且当x=3时有最大值4,试确定这个二次函数的解析式。
1、抛物线的形状、开口方向都与抛物线y=-x2相同顶点在(1,-2),则抛物线的解析式为________________________________.
2、已知二次函数的对称轴是直线x=1,图象上最低点 P的纵坐标式-8,图象还过点(-2,10),设函数表达式____________________________。
3、已知二次函数图像经过点A(1,-2),B(-1,6),C,2,-6),设二次函数表达式_____________。
变式训练
学以致用
如图是一名学生推铅球时,铅球行进高度y(m)与水平距离x(m)的图象,你能求出其表达式吗?
解:由图像知,抛物线的顶点为(4,3),过点(10,0)可设抛物线解析式为
把(10,0)代入上式,得
在确定二次函数的表达式时
(1)若已知图像上三个非特殊点,常设一般式 ;
(2)若已知二次函数顶点坐标或对称轴,或最大值,最小值,常设顶点式 较为简便;
温馨提示
学贵有思
1、本节课你学到了……
2、你还有什么困惑?
选择最优解法,求下列二次函数表达式:
1、已知抛物线的图象经过点(1,1) 、(﹣1,﹣1) 、(0,﹣2) ,设抛物线解析式为___________________
2、已知抛物线的顶点坐标(﹣2,3) ,且经过点(﹣1,0) ,设抛物线解析式为____________________
3、已知二次函数有最大值6,对称轴是直线x=2,设抛物线解析式为____________________
过关一
y=ax2+bx+c(a≠0)
y=a(x+2)2+3(a≠0)
y=a(x-2)2+6(a≠0)
二次函数y=ax2+bx+c的图象过点A(1,0),B(2,0)两点,且经过点(3,4),求这个二次函数的解析式。
课后延伸
谢谢!
温故知新
1.二次函数表达式的一般形式是________________,
顶点坐标是__________________。
二次函数表达式的顶点式是______________。
3.
y=ax2+bx+c(a≠0)
y=a(x-h)2+k
