人教版七年级下册数学课件5.1.2垂线(2课时共49张PPT)
文档属性
| 名称 | 人教版七年级下册数学课件5.1.2垂线(2课时共49张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 00:00:00 | ||
图片预览






文档简介
(共49张PPT)
5.1 相交线
5.1.2 垂线
第一课时
第二课时
人教版 数学 七年级 下册
垂线
第一课时
返回
观察下面图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
导入新知
日常生活里,图中的两条直线的关系很常见,你能再举出其他例子吗?
导入新知
2. 掌握垂直的概念,能根据垂直求出角的度数.
1. 理解垂线的概念,会用三角尺或量角器过一点画已知直线的垂线 .
素养目标
3. 掌握垂线的性质,并会利用所学知识进行简单的推理.
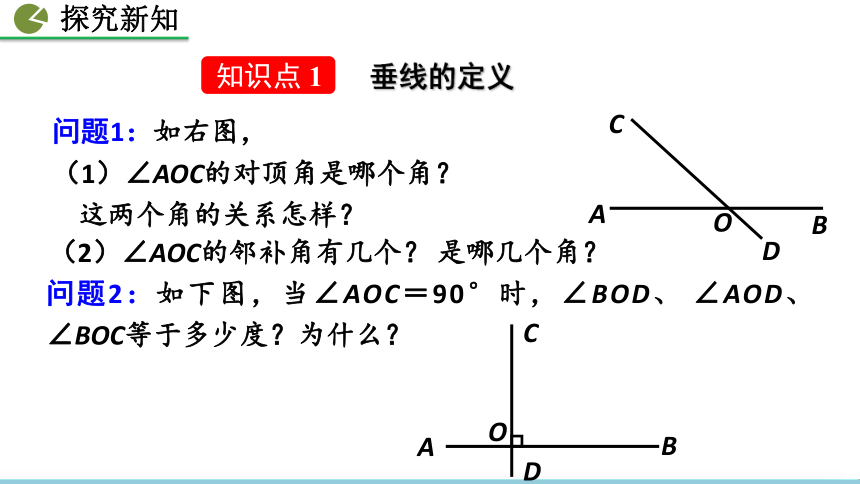
问题1:如右图,
(1)∠AOC的对顶角是哪个角?
这两个角的关系怎样?
(2)∠AOC的邻补角有几个? 是哪几个角?
问题2:如下图,当∠AOC=90°时,∠BOD、 ∠AOD、∠BOC等于多少度?为什么?
探究新知
知识点 1
垂线的定义
A
C
B
D
O
A
B
C
D
O
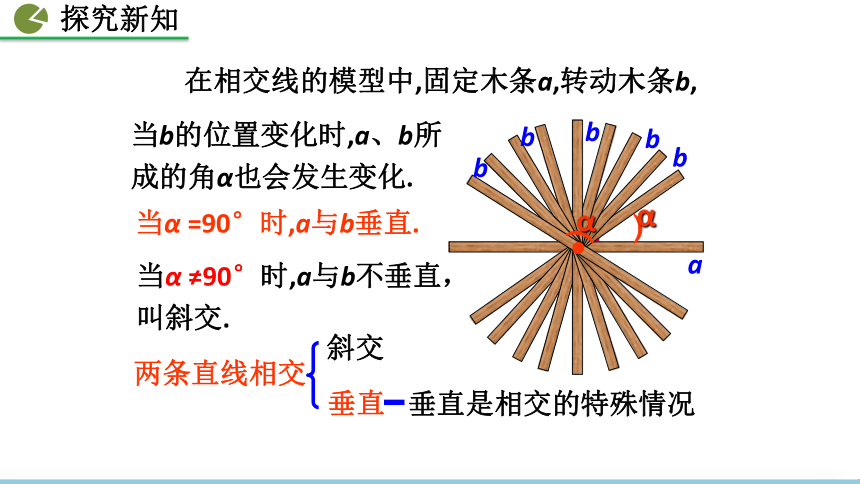
在相交线的模型中,固定木条a,转动木条b,
当α =90°时,a与b垂直.
当b的位置变化时,a、b所成的角α也会发生变化.
当α ≠90°时,a与b不垂直,叫斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况
)
α
a
b
b
b
b
b
)
α
探究新知
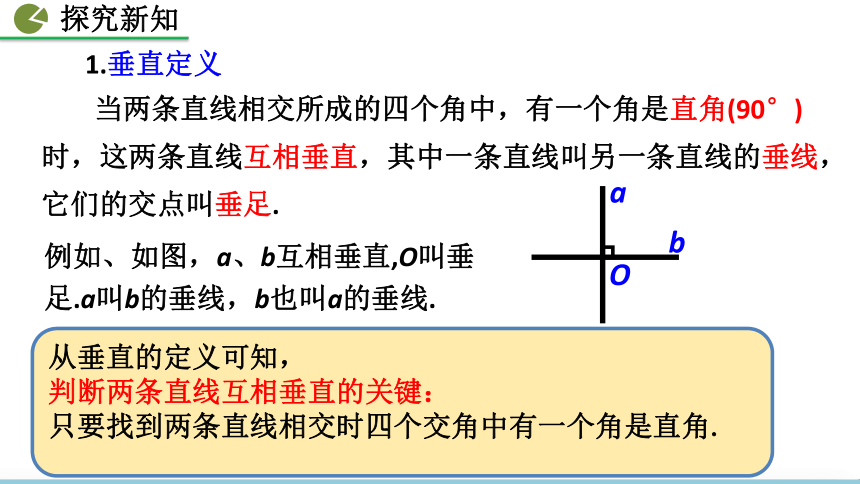
当两条直线相交所成的四个角中,有一个角是直角(90°)时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线.
b
a
O
从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中有一个角是直角.
探究新知
1.垂直定义
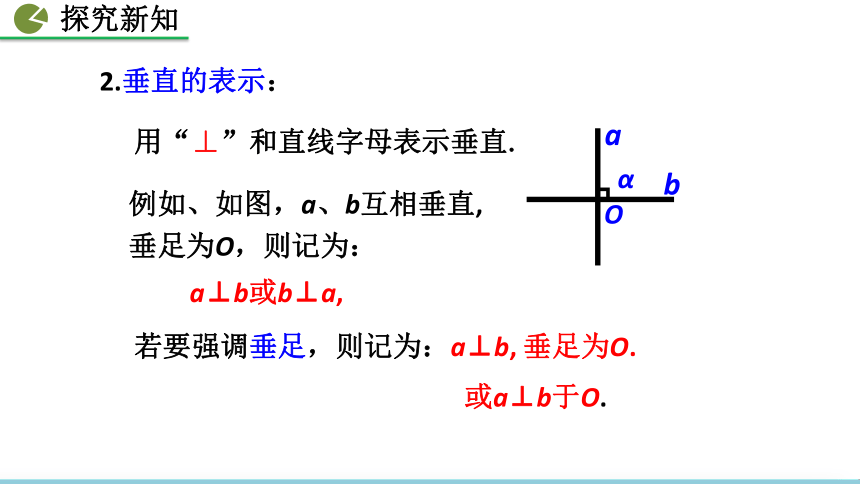
用“⊥”和直线字母表示垂直.
α
2.垂直的表示:
例如、如图,a、b互相垂直, 垂足为O,则记为:
a⊥b或b⊥a,
若要强调垂足,则记为:a⊥b, 垂足为O.
或a⊥b于O.
探究新知
b
a
O
F
E
M
N
O
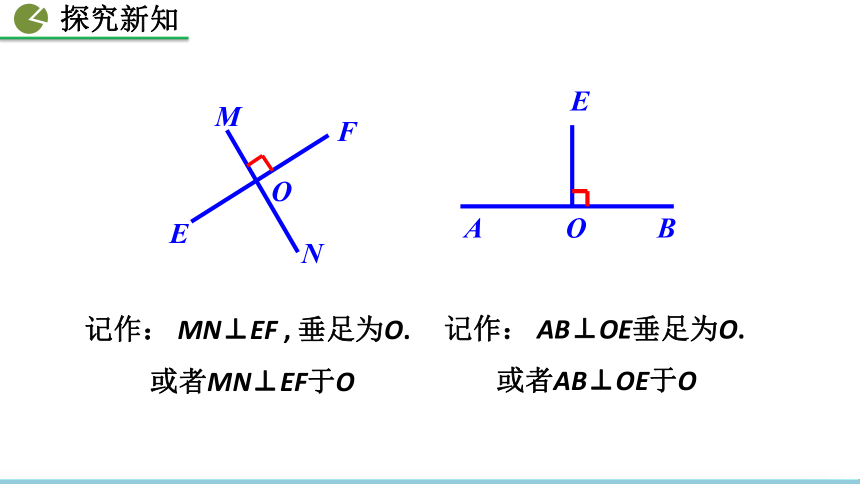
记作: MN⊥EF , 垂足为O.
或者MN⊥EF于O
A
B
O
E
记作: AB⊥OE垂足为O.
或者AB⊥OE于O
探究新知
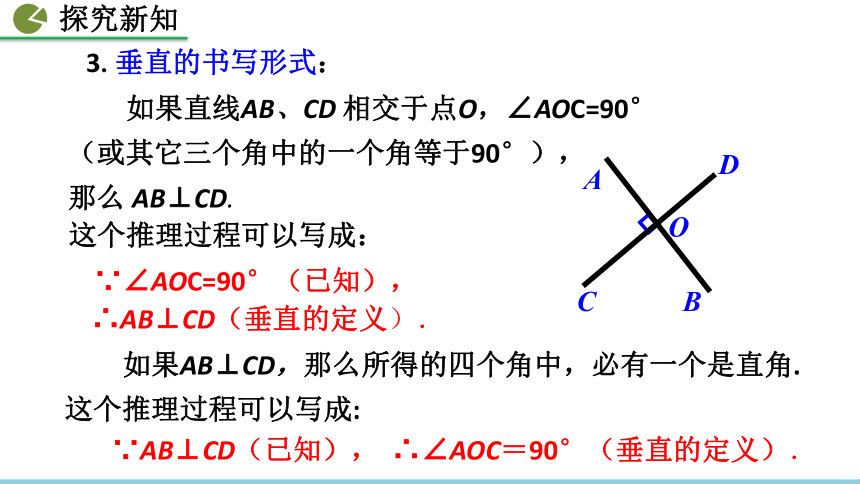
∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义).
如果直线AB、CD 相交于点O,∠AOC=90°
(或其它三个角中的一个角等于90°),
那么 AB⊥CD.
这个推理过程可以写成:
∵AB⊥CD(已知), ∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角. 这个推理过程可以写成:
A
B
C
D
O
3.垂直的书写形式:
探究新知
日常生活中,两条直线互相垂直的情形很常见,说出图中的一些互相垂直的线条.
你能再举出其他例子吗?
探究新知
方格本的横线和竖线
铅垂线和水平线
探究新知
例1 如图AB⊥CD垂足为O,∠COF=56°,求∠AOE?
解:∵AB⊥CD(已知)
∴∠COB=90°(垂直的定义)
∴∠BOF= ∠COB-∠COF
=90°-56°=34°
∴ ∠AOE=∠BOF=34°(对顶角相等)
F
E
D
C
B
A
O
?
56°
探究新知
素养考点 1
利用垂直求角的度数
1. 如图,直线AB、CD相交于点O,OE⊥AB, ∠1=55°,求∠EOD的度数.
∴ ∠EOB=90° (垂直的定义)
∴ ∠EOD =∠EOB +∠BOD
=90°+55°=145°
A
C
E
B
D
O
1
(
∵ AB⊥OE (已知)
∵ ∠BOD =∠1=55° (对顶角相等)
巩固练习
解:
(1)画已知直线l的垂线能画几条?
(2)过直线l上的一点A画l的垂线,这样的垂线能画几条?
(3)过直线l外的一点B画l的垂线,这样的垂线能画几条?
A
.B
l
.
知识点 2
垂线的画法及其性质
探究新知
【讨论】这样画l的垂线可以画几条?
1.放
2.靠
3.画
l
O
如图,已知直线 l,作l的垂线.
A
无数条
探究新知
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l上的一点A ,作l的垂线.
【讨论】这样画l的垂线可以画几条?
一条
探究新知
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l外的一点A ,作l的垂线.
根据以上操作,你能得出什么结论?
【讨论】这样画l的垂线可以画几条?
一条
探究新知
提示:
1.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
2.“有且只有”中,“有”指存在,“只有”指唯一性.
探究新知
在同一平面内,过一点有且只有一条直线与已知直线垂直.
垂线的性质:
(2018?益阳)如图,直线AB、CD相交于点O,EO⊥CD.下列说法错误的是( )
A.∠AOD=∠BOC
B.∠AOE+∠BOD=90°
C.∠AOC=∠AOE
D.∠AOD+∠BOD=180°
巩固练习
连接中考
C
1.下面四种判定两条直线垂直的方法,正确的有( )个
(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直
(2)两条直线相交,只要有一组邻补角相等,则这两条直线互相垂直
(3)两条直线相交,所成的四个角相等,这两条直线互相垂直
(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直
A. 4 B. 3 C. 2 D. 1
A
b
a
课堂检测
基础巩固题
2.过点P 向线段AB 所在直线引垂线,正确的是( )
A B C D
C
课堂检测
基础巩固题
3.如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=58°,则∠BED的度数为 .
C
A
B
E
F
D
32°
课堂检测
基础巩固题
4.如图三角形ABC,根据要求画图:
① 过点A作BC的垂线,垂足为D;
② 过点C作AB的垂线CE,垂足为E.
解:如图
A
C
B
D
E
课堂检测
基础巩固题
如图,直线BC与MN相交于点O,AO⊥BC,∠BOE=∠NOE,若∠EON=20°,求∠AOM和∠NOC的度数.
解:∵∠BOE=∠NOE,∴∠BON=2∠EON=40°,
∴∠NOC=180°-∠BON =180°-40°=140°,
∠MOC=∠BON=40°.
∵AO⊥BC,∴∠AOC=90°,
∴∠AOM=∠AOC-∠MOC=90°-40°=50°,
∴∠NOC=140°,∠AOM=50°.
能力提升题
课堂检测
如图,AO⊥FD,OD为∠BOC的平分线,OE为射线OB的反向延长线,若∠AOB=40°,求∠EOF、∠COE的度数.
A
F
D
O
B
C
E
解:∵AO⊥OD且∠AOB=40°,
∴∠BOD=90°-40°=50°,
∴∠EOF=50°.
又∵OD平分∠BOC,
∴∠DOC=∠BOD=50°,
∴∠COE=180°-50°-50°=80°.
拓广探索题
课堂检测
两条直线相交
一般情况
垂线
对顶角:相等
邻补角:互补
垂线的存在性和唯一性
特殊情况
相交成直角
课堂小结
点到直线的距离
第二课时
返回
∟
在灌溉时,要把河里的水引到农田里的P处,如何挖渠能使渠道最短呢?
导入新知
2. 掌握点到直线的距离的概念,并会度量点到直线的距离.
1. 理解垂线段的概念,会用三角尺或量角器过一点画已知直线的垂线段 .
素养目标
3. 掌握垂线段最短的性质,并会利用所学知识解决简单的实际问题.
有人不慎掉入有鳄鱼的湖中.如图,他在P点,应选择什么样的路线尽快游到岸边m呢?
知识点 1
点到直线的距离
探究新知
连接直线外一点与直线上各点的所有线段中,垂线段最短.
垂线段最短
P
A
B
C
m
D
简单说成:垂线段最短.
垂线的性质2
垂线段
斜线段
∵PB⊥m于B
∴PB探究新知
垂线段是垂线上的一部分,它是线段,一端是一个点,另一端是垂足.
A
B
P
D
特别强调:
垂线
垂线段
探究新知
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
P
m
A
例如:如图,PA⊥m于点A ,垂线段PA的长度叫做点P到直线m的距离.
例 如图,是一个同学跳远的位置,跳远成绩怎么表示?
m
P
A
解:过P点作PA⊥m于点A,
垂线段PA的长度就是
该同学的跳远成绩.
点到直线的距离的概念:
探究新知
B
如图,怎样测量点A 到
直线 m 的距离?
A
m
1.过点A画出直线m的垂线段AB,垂足为B;
2.用刻度尺量出垂线段AB的长度.
0m
20m
30m
10m
探究新知
0cm
20cm
30cm
10cm
例1 如图,(1)画出线段BC的中点M,连结AM;
(2)比较点B与点C到直线AM的距离.
A
B
C
M
P
Q
0cm
20cm
30cm
10cm
0cm
20cm
30cm
10cm
9cm
9cm
∴BP=CQ
探究新知
素养考点 1
画出点到直线的距离
1.如图,点M、N分别在直线AB、CD上,用三角板画图,
1)过点M画CD的垂线交CD于点F,
2)点M和点N的距离是线段____的长,
3)点M到CD的距离是线段____的长.
MN
MF
A
B
C
D
M
N
F
巩固练习
C
A
B
0m
20m
30m
10m
0m
20m
30m
10m
8m
25m
例2 如图,量出
(1)村庄A与货场B的距离,
(2)货场B到铁道的距离.
素养考点 2
测量点线间距离
探究新知
2.马路两旁两名同学A、B,若A同学到马路对边怎样走最近?若A同学到B同学处怎样走最近?
解:过点A作AC⊥BC,垂足为C,A同学沿着AC走到路对面最近,根据
A
B
C
连接AB, A同学沿着AB走到B同学处最近,根据
垂线段最短.
两点之间线段最短.
巩固练习
(2019?常州)如图,在线段PA、PB、PC、PD中,长度最小的是( )
A.线段PA B.线段PB C.线段PC D.线段PD
巩固练习
连接中考
B
1.如图,下列说法正确的是( )
A.线段AB叫做点B到直线AC的距离
B.线段AB的长度叫作点A到直线AC的距离
C.线段BD的长度叫作点D到直线BC的距离
D.线段BD的长度叫作点B到直线AC的距离
A
B
C
D
D
基础巩固题
课堂检测
2.如图, AC⊥BC, ∠C=90° ,线段AC、BC、CD中最短的是( )
A. AC B. BC
C. CD D. 不能确定
D
A
B
C
C
课堂检测
基础巩固题
3.若点P是直线m外一点,点A,B,C分别是直线m上不同的三点,且PA=5,PB=6,PC=7,则点P到直线m的距离不可能是 ( )
A. 3 B. 4 C. 5 D. 6
D
课堂检测
基础巩固题
4.如图三角形ABC,根据要求画图:
① 过点B画出点B到AC的垂线段BF
解:如图
A
C
B
F
课堂检测
基础巩固题
如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由。
张庄
解:火车站建在D处,理由是:垂线段最短.
D
能力提升题
课堂检测
?? 如图,AC⊥BC于C,CD⊥AB于D,DE⊥BC于E.试比较四条线段AC,CD,DE和AB的大小.
解:∵ AC⊥BC于C,(已知)
∴ AC<AB.(垂线的性质二)
又∵ CD⊥AD于D,(已知)
∴ CD<AC.(垂线的性质二)
∵ DE⊥CE于E,(已知)
∴ DE<CD.(垂线的性质二)
∴ AB>AC>CD>DE.
拓广探索题
课堂检测
两条直线相交
一般情况
垂线
对顶角:相等
邻补角:互补
垂线的存在性和唯一性
特殊情况
相交成直角
课堂小结
垂线段最短
点到直线的距离
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
5.1 相交线
5.1.2 垂线
第一课时
第二课时
人教版 数学 七年级 下册
垂线
第一课时
返回
观察下面图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
导入新知
日常生活里,图中的两条直线的关系很常见,你能再举出其他例子吗?
导入新知
2. 掌握垂直的概念,能根据垂直求出角的度数.
1. 理解垂线的概念,会用三角尺或量角器过一点画已知直线的垂线 .
素养目标
3. 掌握垂线的性质,并会利用所学知识进行简单的推理.
问题1:如右图,
(1)∠AOC的对顶角是哪个角?
这两个角的关系怎样?
(2)∠AOC的邻补角有几个? 是哪几个角?
问题2:如下图,当∠AOC=90°时,∠BOD、 ∠AOD、∠BOC等于多少度?为什么?
探究新知
知识点 1
垂线的定义
A
C
B
D
O
A
B
C
D
O
在相交线的模型中,固定木条a,转动木条b,
当α =90°时,a与b垂直.
当b的位置变化时,a、b所成的角α也会发生变化.
当α ≠90°时,a与b不垂直,叫斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况
)
α
a
b
b
b
b
b
)
α
探究新知
当两条直线相交所成的四个角中,有一个角是直角(90°)时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线.
b
a
O
从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中有一个角是直角.
探究新知
1.垂直定义
用“⊥”和直线字母表示垂直.
α
2.垂直的表示:
例如、如图,a、b互相垂直, 垂足为O,则记为:
a⊥b或b⊥a,
若要强调垂足,则记为:a⊥b, 垂足为O.
或a⊥b于O.
探究新知
b
a
O
F
E
M
N
O
记作: MN⊥EF , 垂足为O.
或者MN⊥EF于O
A
B
O
E
记作: AB⊥OE垂足为O.
或者AB⊥OE于O
探究新知
∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义).
如果直线AB、CD 相交于点O,∠AOC=90°
(或其它三个角中的一个角等于90°),
那么 AB⊥CD.
这个推理过程可以写成:
∵AB⊥CD(已知), ∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角. 这个推理过程可以写成:
A
B
C
D
O
3.垂直的书写形式:
探究新知
日常生活中,两条直线互相垂直的情形很常见,说出图中的一些互相垂直的线条.
你能再举出其他例子吗?
探究新知
方格本的横线和竖线
铅垂线和水平线
探究新知
例1 如图AB⊥CD垂足为O,∠COF=56°,求∠AOE?
解:∵AB⊥CD(已知)
∴∠COB=90°(垂直的定义)
∴∠BOF= ∠COB-∠COF
=90°-56°=34°
∴ ∠AOE=∠BOF=34°(对顶角相等)
F
E
D
C
B
A
O
?
56°
探究新知
素养考点 1
利用垂直求角的度数
1. 如图,直线AB、CD相交于点O,OE⊥AB, ∠1=55°,求∠EOD的度数.
∴ ∠EOB=90° (垂直的定义)
∴ ∠EOD =∠EOB +∠BOD
=90°+55°=145°
A
C
E
B
D
O
1
(
∵ AB⊥OE (已知)
∵ ∠BOD =∠1=55° (对顶角相等)
巩固练习
解:
(1)画已知直线l的垂线能画几条?
(2)过直线l上的一点A画l的垂线,这样的垂线能画几条?
(3)过直线l外的一点B画l的垂线,这样的垂线能画几条?
A
.B
l
.
知识点 2
垂线的画法及其性质
探究新知
【讨论】这样画l的垂线可以画几条?
1.放
2.靠
3.画
l
O
如图,已知直线 l,作l的垂线.
A
无数条
探究新知
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l上的一点A ,作l的垂线.
【讨论】这样画l的垂线可以画几条?
一条
探究新知
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l外的一点A ,作l的垂线.
根据以上操作,你能得出什么结论?
【讨论】这样画l的垂线可以画几条?
一条
探究新知
提示:
1.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
2.“有且只有”中,“有”指存在,“只有”指唯一性.
探究新知
在同一平面内,过一点有且只有一条直线与已知直线垂直.
垂线的性质:
(2018?益阳)如图,直线AB、CD相交于点O,EO⊥CD.下列说法错误的是( )
A.∠AOD=∠BOC
B.∠AOE+∠BOD=90°
C.∠AOC=∠AOE
D.∠AOD+∠BOD=180°
巩固练习
连接中考
C
1.下面四种判定两条直线垂直的方法,正确的有( )个
(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直
(2)两条直线相交,只要有一组邻补角相等,则这两条直线互相垂直
(3)两条直线相交,所成的四个角相等,这两条直线互相垂直
(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直
A. 4 B. 3 C. 2 D. 1
A
b
a
课堂检测
基础巩固题
2.过点P 向线段AB 所在直线引垂线,正确的是( )
A B C D
C
课堂检测
基础巩固题
3.如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=58°,则∠BED的度数为 .
C
A
B
E
F
D
32°
课堂检测
基础巩固题
4.如图三角形ABC,根据要求画图:
① 过点A作BC的垂线,垂足为D;
② 过点C作AB的垂线CE,垂足为E.
解:如图
A
C
B
D
E
课堂检测
基础巩固题
如图,直线BC与MN相交于点O,AO⊥BC,∠BOE=∠NOE,若∠EON=20°,求∠AOM和∠NOC的度数.
解:∵∠BOE=∠NOE,∴∠BON=2∠EON=40°,
∴∠NOC=180°-∠BON =180°-40°=140°,
∠MOC=∠BON=40°.
∵AO⊥BC,∴∠AOC=90°,
∴∠AOM=∠AOC-∠MOC=90°-40°=50°,
∴∠NOC=140°,∠AOM=50°.
能力提升题
课堂检测
如图,AO⊥FD,OD为∠BOC的平分线,OE为射线OB的反向延长线,若∠AOB=40°,求∠EOF、∠COE的度数.
A
F
D
O
B
C
E
解:∵AO⊥OD且∠AOB=40°,
∴∠BOD=90°-40°=50°,
∴∠EOF=50°.
又∵OD平分∠BOC,
∴∠DOC=∠BOD=50°,
∴∠COE=180°-50°-50°=80°.
拓广探索题
课堂检测
两条直线相交
一般情况
垂线
对顶角:相等
邻补角:互补
垂线的存在性和唯一性
特殊情况
相交成直角
课堂小结
点到直线的距离
第二课时
返回
∟
在灌溉时,要把河里的水引到农田里的P处,如何挖渠能使渠道最短呢?
导入新知
2. 掌握点到直线的距离的概念,并会度量点到直线的距离.
1. 理解垂线段的概念,会用三角尺或量角器过一点画已知直线的垂线段 .
素养目标
3. 掌握垂线段最短的性质,并会利用所学知识解决简单的实际问题.
有人不慎掉入有鳄鱼的湖中.如图,他在P点,应选择什么样的路线尽快游到岸边m呢?
知识点 1
点到直线的距离
探究新知
连接直线外一点与直线上各点的所有线段中,垂线段最短.
垂线段最短
P
A
B
C
m
D
简单说成:垂线段最短.
垂线的性质2
垂线段
斜线段
∵PB⊥m于B
∴PB
垂线段是垂线上的一部分,它是线段,一端是一个点,另一端是垂足.
A
B
P
D
特别强调:
垂线
垂线段
探究新知
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
P
m
A
例如:如图,PA⊥m于点A ,垂线段PA的长度叫做点P到直线m的距离.
例 如图,是一个同学跳远的位置,跳远成绩怎么表示?
m
P
A
解:过P点作PA⊥m于点A,
垂线段PA的长度就是
该同学的跳远成绩.
点到直线的距离的概念:
探究新知
B
如图,怎样测量点A 到
直线 m 的距离?
A
m
1.过点A画出直线m的垂线段AB,垂足为B;
2.用刻度尺量出垂线段AB的长度.
0m
20m
30m
10m
探究新知
0cm
20cm
30cm
10cm
例1 如图,(1)画出线段BC的中点M,连结AM;
(2)比较点B与点C到直线AM的距离.
A
B
C
M
P
Q
0cm
20cm
30cm
10cm
0cm
20cm
30cm
10cm
9cm
9cm
∴BP=CQ
探究新知
素养考点 1
画出点到直线的距离
1.如图,点M、N分别在直线AB、CD上,用三角板画图,
1)过点M画CD的垂线交CD于点F,
2)点M和点N的距离是线段____的长,
3)点M到CD的距离是线段____的长.
MN
MF
A
B
C
D
M
N
F
巩固练习
C
A
B
0m
20m
30m
10m
0m
20m
30m
10m
8m
25m
例2 如图,量出
(1)村庄A与货场B的距离,
(2)货场B到铁道的距离.
素养考点 2
测量点线间距离
探究新知
2.马路两旁两名同学A、B,若A同学到马路对边怎样走最近?若A同学到B同学处怎样走最近?
解:过点A作AC⊥BC,垂足为C,A同学沿着AC走到路对面最近,根据
A
B
C
连接AB, A同学沿着AB走到B同学处最近,根据
垂线段最短.
两点之间线段最短.
巩固练习
(2019?常州)如图,在线段PA、PB、PC、PD中,长度最小的是( )
A.线段PA B.线段PB C.线段PC D.线段PD
巩固练习
连接中考
B
1.如图,下列说法正确的是( )
A.线段AB叫做点B到直线AC的距离
B.线段AB的长度叫作点A到直线AC的距离
C.线段BD的长度叫作点D到直线BC的距离
D.线段BD的长度叫作点B到直线AC的距离
A
B
C
D
D
基础巩固题
课堂检测
2.如图, AC⊥BC, ∠C=90° ,线段AC、BC、CD中最短的是( )
A. AC B. BC
C. CD D. 不能确定
D
A
B
C
C
课堂检测
基础巩固题
3.若点P是直线m外一点,点A,B,C分别是直线m上不同的三点,且PA=5,PB=6,PC=7,则点P到直线m的距离不可能是 ( )
A. 3 B. 4 C. 5 D. 6
D
课堂检测
基础巩固题
4.如图三角形ABC,根据要求画图:
① 过点B画出点B到AC的垂线段BF
解:如图
A
C
B
F
课堂检测
基础巩固题
如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由。
张庄
解:火车站建在D处,理由是:垂线段最短.
D
能力提升题
课堂检测
?? 如图,AC⊥BC于C,CD⊥AB于D,DE⊥BC于E.试比较四条线段AC,CD,DE和AB的大小.
解:∵ AC⊥BC于C,(已知)
∴ AC<AB.(垂线的性质二)
又∵ CD⊥AD于D,(已知)
∴ CD<AC.(垂线的性质二)
∵ DE⊥CE于E,(已知)
∴ DE<CD.(垂线的性质二)
∴ AB>AC>CD>DE.
拓广探索题
课堂检测
两条直线相交
一般情况
垂线
对顶角:相等
邻补角:互补
垂线的存在性和唯一性
特殊情况
相交成直角
课堂小结
垂线段最短
点到直线的距离
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
