人教版高中物理必修二讲义资料,复习补习资料:57圆周运动的实例分析(提高)
文档属性
| 名称 | 人教版高中物理必修二讲义资料,复习补习资料:57圆周运动的实例分析(提高) |  | |
| 格式 | zip | ||
| 文件大小 | 364.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-11-25 21:18:32 | ||
图片预览



文档简介
生活中的圆周运动
【学习目标】
1、能够根据圆周运动的规律,熟练地运用动力学的基本方法解决圆周运动问题。
2、学会分析圆周运动的临界状态的方法,理解临界状态并利用临界状态解决圆周运动问题。
3、理解外力所能提供的向心力和做圆周运动所需要的向心力之间的关系,以此为根据理解向心运动和离心运动。
【巩固练习】
一、选择题:
1、如图所示,一个球绕中心轴线以角速度ω做匀速圆周转动,则( )
A.a、b两点线速度相同
B.a、b两点角速度相同
C.若θ=30°,则a、b两点的速度之比
D.若θ=30°,则a、b两点的向心加速度之比
2、如图所示,质量为m的物块,沿着半径为R的半球形金属壳内壁滑下,半球形金属壳竖直放置,开口向上,滑到最低点时速度大小为v,物块与球壳之间的摩擦因数为,则物块在最低点时,下列说法正确的是( )
A.受到的向心力是 B.受到的摩擦力为
C.受到的摩擦力为 D.受到的合力方向为斜向左上方
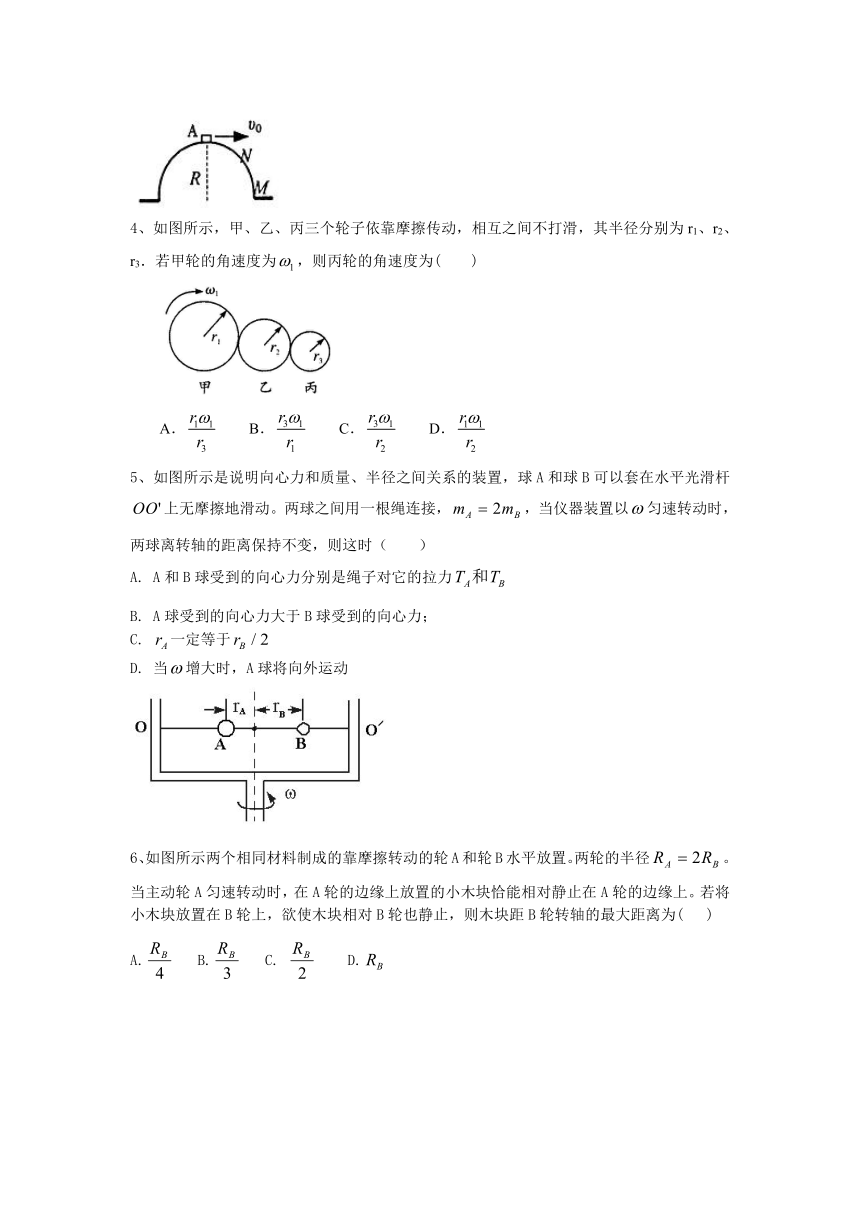
3、如图所示,半径为R的光滑半圆球固定在水平面上,顶部有一小物体A。今给它一个水平初速度,则物体将( )
A. 沿球面下滑至M点
B. 沿球面下滑至某一点N,便离开球面做斜下抛运动
C. 按半径大于R的新的圆弧轨道做圆周运动
D. 立即离开半圆球面做平抛运动
4、如图所示,甲、乙、丙三个轮子依靠摩擦传动,相互之间不打滑,其半径分别为r1、r2、r3.若甲轮的角速度为,则丙轮的角速度为( )
A. B. C. D.
5、如图所示是说明向心力和质量、半径之间关系的装置,球A和球B可以套在水平光滑杆上无摩擦地滑动。两球之间用一根绳连接,,当仪器装置以匀速转动时,两球离转轴的距离保持不变,则这时( )
A. A和B球受到的向心力分别是绳子对它的拉力
B. A球受到的向心力大于B球受到的向心力;
C. 一定等于
D. 当增大时,A球将向外运动
6、如图所示两个相同材料制成的靠摩擦转动的轮A和轮B水平放置。两轮的半径。当主动轮A匀速转动时,在A轮的边缘上放置的小木块恰能相对静止在A轮的边缘上。若将小木块放置在B轮上,欲使木块相对B轮也静止,则木块距B轮转轴的最大距离为( )
A. B. C. D.
7、(2019 红桥区模拟)如图所示,长为的细杆一端固定一个质量为m的小球,使之绕另一端O在竖直面内做圆周运动,小球运动到最高点时的速度,物体在这点时( )
A.小球对细杆的拉力是
B.小球对杆的压力是
C.小球对细杆的拉力是
D.小球对杆的压力是
8、(2019 南京市模拟试卷)2013年6月11日,我国航天员聂海胜、张晓光和王亚平在“天宫一号”首次为青少年进行太空授课,开辟了我国太空教育的新篇章,在天宫一号里,长为三的细线一端固定,另一端系一个小球,拉直细线,让小球在B点以垂直于细线的速度v0开始做圆周运动,如图所示,设卫星轨道处重力加速度为g',在小球运动的过程中,下列说法正确的是( )
A.小球做速率变化的圆周运动
B.细线拉力的大小不断变化
C.只要v0>0,小球都能通过A点
D.只有,小球才能通过A点
二、填空题:
1、质量m的小球用细线悬于O点且可在竖直平面内做圆周运动,到达最高点时的速度,此时细线的张力是___________,若到达最高点的速度,则此时细线的张力是__________(假设细线未断)。
2、如图所示,半径为R的圆盘绕垂直于盘面的中心轴匀速转动,其正上方h处沿OB方向水平抛出一小球,要使球与盘只碰一次,且落点为B,则小球的初速度v=________,圆盘转动的角速度________.
3、如图(1)是利用激光测转速的原理示意图,图中圆盘可绕固定轴转动,盘边缘侧面上有一小段涂有很薄的反光材料.当盘转到某一位置时,接收器可以接收反光涂层所反射的激光束,并将所收到的光信号转变成电信号,在示波器显示屏上显示出来[如图(2)所示].
(1)若图(2)中示波器显示屏横向的每大格(5小格)对应的时间为5.00×s,则圆盘的转速为_____r/s.(保留3位有效数字)
(2)若测得圆盘直径为10.20 cm,则可求得圆盘侧面反光涂层的长度为________cm.(保留3位有效数字)
三、计算题:
1、如图所示,竖直圆筒内壁光滑,半径为R,顶部有入口A,在A的正下方h处有出口B,一质量为m的小球从A处沿着切线方向的水平槽射入桶内,要使球从B处飞出,小球射入A的速度应该满足什么条件?在运动过程中球对桶的压力多大?
2、飞行员从俯冲状态往上拉时,会发生黑视,第一次是因为血压降低,导致视网膜缺血,第二次是因为大脑缺血,问:
(1)血压为什么会降低?
(2)血液在人体中起的作用是什么?
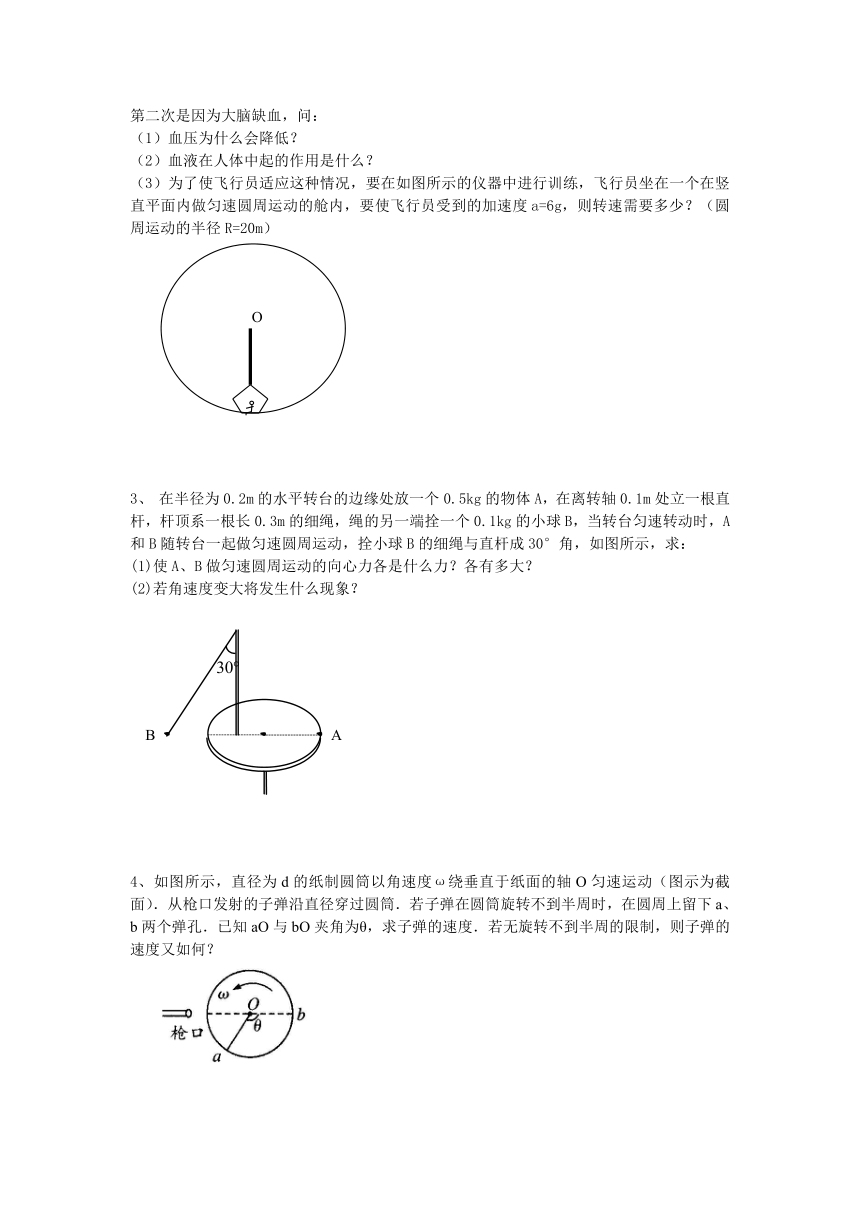
(3)为了使飞行员适应这种情况,要在如图所示的仪器中进行训练,飞行员坐在一个在竖直平面内做匀速圆周运动的舱内,要使飞行员受到的加速度a=6g,则转速需要多少?(圆周运动的半径R=20m)
3、 在半径为0.2m的水平转台的边缘处放一个0.5kg的物体A,在离转轴0.1m处立一根直杆,杆顶系一根长0.3m的细绳,绳的另一端拴一个0.1kg的小球B,当转台匀速转动时,A和B随转台一起做匀速圆周运动,拴小球B的细绳与直杆成30°角,如图所示,求:
(1)使A、B做匀速圆周运动的向心力各是什么力?各有多大?
(2)若角速度变大将发生什么现象?
4、如图所示,直径为d的纸制圆筒以角速度ω绕垂直于纸面的轴O匀速运动(图示为截面).从枪口发射的子弹沿直径穿过圆筒.若子弹在圆筒旋转不到半周时,在圆周上留下a、b两个弹孔.已知aO与bO夹角为θ,求子弹的速度.若无旋转不到半周的限制,则子弹的速度又如何?
5、(2019 太原五中高三第一次段考)物体做圆周运动时所需的向心力F需由物体运动情况决定,合力提供的向心力F供由物体受力情况决定。若某时刻F需=F供,则物体能做圆周运动;若F需>F供,物体将做离心运动;若F需<F供,物体将做近心运动。现有一根长L=0.5 m的刚性轻绳,其一端固定于O点,另一端系着质量m=1 kg的小球(可视为质点),将小球提至O点正上方的A点处,此时绳刚好伸直且无张力,如图所示。不计空气阻力,g取10 m/s2,则:
(1)在小球以速度v1=5 m/s水平抛出的瞬间,绳中的张力为多少?
(2)在小球以速度v2=1 m/s水平抛出的瞬间,绳中若有张力,求其大小;若无张力,试求轻绳再次伸直时所经历的时间。
6、如图所示为录音机在工作时的示意图,轮子1是主动轮,轮子2为从动轮,轮1和轮2就是磁带盒内的两个转盘,空带一边半径为r1=0.5cm,满带一边半径为r2=3cm,已知主动轮转速不变,恒为n1=36 r/min,试求:
(1)从动轮2的转速变化范围;
(2)磁带运动的速度变化范围.
【答案及解析】
一、选择题:
1、B、C、D
解析:由于a、b两点在同一球上,因此a、b两点的角速度ω相同,选项B正确;而据v=ωr可知,选项A错误;由几何关系有,当θ=30°时,,则,选项C正确;由,可知,选项D正确.
2、D
解析:物体在最低点的向心力是,所以选项A错误;
受到的摩擦力是,所以BC选项都错误;
因为物块受到水平向左的摩擦力和竖直向上的向心力,这两个力的合力就是物块受到的合力,所以合力的方向是斜向左上方,D选项正确。
3、D
解析:对小物体在顶部A处用牛顿第二定律,将代入上式得到,球面对球的支持力F=0,因此,小球在不计空气阻力的情况下,只受重力以水平速度抛出,做平抛运动,所以D选项正确。
4、A
解析:本题属于摩擦传动,摩擦传动的特点是各个轮边缘的线速度大小相等,即v1=v2=v3,即有,显然选项A正确.
5、AC
解析:A、B两个球受到的向心力是一对相互作用力,且相同的时间转过的角度一定相同,所以;由向心力公式可知,它们的轨道半径与其质量成反比,所以一定等于,选项AC正确。只要A、B两个球的轨道半径满足与质量成反比关系,无论角速度多大,两个小球总是保持在原来的轨道上运动,既不离心运动也不会向心运动。
6、C
解析:由图可知,主动轮A匀速转动时,A、B两轮边缘上的点的线速度大小相等,由
由于小木块恰能在A轮边缘上静止,,则由静摩擦力提供的向心力达到最大值 。
设小木块放在B轮上能使木块相对静止的距B转轴的最大距离为r,则向心力由最大静摩擦力提供,故,所以选项C正确。
7、B
解析:球在最高点对杆恰好无压力时,重力提供向心力,根据牛顿第二定律,有:,解得:,由于,故杆对球有支持力,根据牛顿第二定律,有:,解得:,根据牛顿第三定律,球对杆由向下的压力,大小为,故选B。
8、C
解析:绳子拉力时刻与速度方向垂直,只改变速度的方向不改变速度的大小,故小球做匀速圆周运动,故A错误;
,v与L不变,故细线拉力的大小不变,B错误;
小球做匀速圆周运动时,绳子的拉力提供向心力,只要v0>0,小球都能通过A点,故C正确,D错误,故选C。
二、填空题:
1、0,3mg
解析:当球的线速度时,对小球在最高点处用牛顿第二定律:,解得线的拉力是;
当球的线速度时,对小球在最高点处用牛顿第二定律:,解得线的拉力是;
2、 (n=1,2,3,…)
解析:小球做平抛运动,在竖直方向上,则运动时间,则运动时间.
又因为水平位移为R,
所以球的速度.
在时间t内盘转过的角度,
又因为,则转盘角速度
.
3、(1)4.55 (2)1.46
解析:(1)转速,,
由图可知:T=0.22s,.
(2)每个周期内接收到信号的时间,
弧长,,
可得1.46 cm.
三、计算题:
1、(1) 球自由落体运动到桶底的时间t必须是圆周运动周期T的整数倍。
(2)
解析:小球射入桶内的运动可以分解为两个分运动:一个是水平面内的匀速圆周运动,一个是竖直方向上的自由落体运动。要使得小球从B处射出,必须满足的条件是小球落到桶底的这段时间内,水平方向完成了整数个圆周,也就是说,球自由落体运动到桶底的时间t必须是圆周运动周期T的整数倍。
在竖直方向:
在水平方向:
解得小球射入速度是
在水平方向球对桶壁的压力大小等于桶壁对于球的弹力,这个弹力提供向心力使球在水平面内做匀速圆周运动,由牛顿第二定律得
2、解析:(1)飞机从俯冲状态往上拉时,人体处于超重状态,血液因为离心运动而向人体的下部分聚集,心脏不能像平常状态运输血液,导致血压降低。
(2)血液在人体中的作用是:通过血液循环,将从肺部获取的氧气,以及从消化器官获取的营养,运送到人体的各个器官,供给生理活动需要,并带走代谢所产生的废物。
(3)由向心加速度的计算公式可得:
仪器的转速
3、解析:(1)物体A随转台一起做匀速圆周运动,和转台保持相对静止,重力跟支持力平衡,转台对A的静摩擦力就是使A做匀速圆周运动所需向心力,如图所示。
设转动时角速度为, 则有:
①
小球B由绳子拴着随转台转动做匀速圆周运动时,它所需的向心力是它的重力和绳子对它的拉力的合力,即:
②
从②式得:
rad/s
rad/s
所以:
(2)如果角速度增大,则A和B所需的向心力也相应增大。A的向心力是转台对它的静摩擦力,在最大静摩擦力的范围内,物体A仍将随转台转动而做匀速圆周运动。由于,当时,静摩擦力就不足以提供A所需的向心力,物体A就将脱离转台沿切线方向飞出。
当角速增大时,物体B将升高,绳子和直杆间的夹角增大,这样它的重力和绳子对它的拉力的合力也相应增大,以适应所需向心力的增大;角速度愈大,B将升得愈高,张角也愈大。由于B的升高,拉力随之增大,如果越过了绳所能承受的最大拉力,绳将被拉断而B即沿切线方向飞出。
4、 (n=0,1,2,…).
解析:设子弹速度为v,则子弹穿过圆筒的时间.
此时间内圆筒转过的角度.
据,得.
则子弹的速度.
本题中若无旋转不到半圆的限制,则在时间t内转过的角度.
则子弹的速度(n=0,1,2,…).
5、解析:(1)要使小球在竖直面内能够做完整的圆周运动,在最高点时至少应该是重力作为所需要的向心力,所以由得:
因为v1>v0,故绳中有张力,由牛顿第二定律得:
代入数据解得,绳中的张力为:T=40 N
(2)因为v2<v0,故绳中没有张力,小球将做平抛运动,如图所示,
水平方向:x=v2t
竖直方向:
L2=(y-L)2+x2
代入数据解得:t=0.4 s
6、(1)6 r/min~216 r/min(2)0.019 m/s~0.113 m/s
解析:本题应抓住主动轮(r1)的角速度恒定不变这一特征,再根据同一时刻两轮磁带走动的线速度相等,从磁带转动时半径的变化来求解.
(1)因为,且两轮边缘上各点的线速度相等,所以,即.
当r2=3cm时,从动轮2的转速最小,.当磁带走完,即r2=0.5cm,r1=3cm时,从动轮2的转速最大,为,故从动轮2的转速变化范围是6 r/min~216 r/min.
(2)由得知:
cm时,,
cm时,.
故磁带的速度变化范围是0.019 m/s~0.113 m/s.
【学习目标】
1、能够根据圆周运动的规律,熟练地运用动力学的基本方法解决圆周运动问题。
2、学会分析圆周运动的临界状态的方法,理解临界状态并利用临界状态解决圆周运动问题。
3、理解外力所能提供的向心力和做圆周运动所需要的向心力之间的关系,以此为根据理解向心运动和离心运动。
【巩固练习】
一、选择题:
1、如图所示,一个球绕中心轴线以角速度ω做匀速圆周转动,则( )
A.a、b两点线速度相同
B.a、b两点角速度相同
C.若θ=30°,则a、b两点的速度之比
D.若θ=30°,则a、b两点的向心加速度之比
2、如图所示,质量为m的物块,沿着半径为R的半球形金属壳内壁滑下,半球形金属壳竖直放置,开口向上,滑到最低点时速度大小为v,物块与球壳之间的摩擦因数为,则物块在最低点时,下列说法正确的是( )
A.受到的向心力是 B.受到的摩擦力为
C.受到的摩擦力为 D.受到的合力方向为斜向左上方
3、如图所示,半径为R的光滑半圆球固定在水平面上,顶部有一小物体A。今给它一个水平初速度,则物体将( )
A. 沿球面下滑至M点
B. 沿球面下滑至某一点N,便离开球面做斜下抛运动
C. 按半径大于R的新的圆弧轨道做圆周运动
D. 立即离开半圆球面做平抛运动
4、如图所示,甲、乙、丙三个轮子依靠摩擦传动,相互之间不打滑,其半径分别为r1、r2、r3.若甲轮的角速度为,则丙轮的角速度为( )
A. B. C. D.
5、如图所示是说明向心力和质量、半径之间关系的装置,球A和球B可以套在水平光滑杆上无摩擦地滑动。两球之间用一根绳连接,,当仪器装置以匀速转动时,两球离转轴的距离保持不变,则这时( )
A. A和B球受到的向心力分别是绳子对它的拉力
B. A球受到的向心力大于B球受到的向心力;
C. 一定等于
D. 当增大时,A球将向外运动
6、如图所示两个相同材料制成的靠摩擦转动的轮A和轮B水平放置。两轮的半径。当主动轮A匀速转动时,在A轮的边缘上放置的小木块恰能相对静止在A轮的边缘上。若将小木块放置在B轮上,欲使木块相对B轮也静止,则木块距B轮转轴的最大距离为( )
A. B. C. D.
7、(2019 红桥区模拟)如图所示,长为的细杆一端固定一个质量为m的小球,使之绕另一端O在竖直面内做圆周运动,小球运动到最高点时的速度,物体在这点时( )
A.小球对细杆的拉力是
B.小球对杆的压力是
C.小球对细杆的拉力是
D.小球对杆的压力是
8、(2019 南京市模拟试卷)2013年6月11日,我国航天员聂海胜、张晓光和王亚平在“天宫一号”首次为青少年进行太空授课,开辟了我国太空教育的新篇章,在天宫一号里,长为三的细线一端固定,另一端系一个小球,拉直细线,让小球在B点以垂直于细线的速度v0开始做圆周运动,如图所示,设卫星轨道处重力加速度为g',在小球运动的过程中,下列说法正确的是( )
A.小球做速率变化的圆周运动
B.细线拉力的大小不断变化
C.只要v0>0,小球都能通过A点
D.只有,小球才能通过A点
二、填空题:
1、质量m的小球用细线悬于O点且可在竖直平面内做圆周运动,到达最高点时的速度,此时细线的张力是___________,若到达最高点的速度,则此时细线的张力是__________(假设细线未断)。
2、如图所示,半径为R的圆盘绕垂直于盘面的中心轴匀速转动,其正上方h处沿OB方向水平抛出一小球,要使球与盘只碰一次,且落点为B,则小球的初速度v=________,圆盘转动的角速度________.
3、如图(1)是利用激光测转速的原理示意图,图中圆盘可绕固定轴转动,盘边缘侧面上有一小段涂有很薄的反光材料.当盘转到某一位置时,接收器可以接收反光涂层所反射的激光束,并将所收到的光信号转变成电信号,在示波器显示屏上显示出来[如图(2)所示].
(1)若图(2)中示波器显示屏横向的每大格(5小格)对应的时间为5.00×s,则圆盘的转速为_____r/s.(保留3位有效数字)
(2)若测得圆盘直径为10.20 cm,则可求得圆盘侧面反光涂层的长度为________cm.(保留3位有效数字)
三、计算题:
1、如图所示,竖直圆筒内壁光滑,半径为R,顶部有入口A,在A的正下方h处有出口B,一质量为m的小球从A处沿着切线方向的水平槽射入桶内,要使球从B处飞出,小球射入A的速度应该满足什么条件?在运动过程中球对桶的压力多大?
2、飞行员从俯冲状态往上拉时,会发生黑视,第一次是因为血压降低,导致视网膜缺血,第二次是因为大脑缺血,问:
(1)血压为什么会降低?
(2)血液在人体中起的作用是什么?
(3)为了使飞行员适应这种情况,要在如图所示的仪器中进行训练,飞行员坐在一个在竖直平面内做匀速圆周运动的舱内,要使飞行员受到的加速度a=6g,则转速需要多少?(圆周运动的半径R=20m)
3、 在半径为0.2m的水平转台的边缘处放一个0.5kg的物体A,在离转轴0.1m处立一根直杆,杆顶系一根长0.3m的细绳,绳的另一端拴一个0.1kg的小球B,当转台匀速转动时,A和B随转台一起做匀速圆周运动,拴小球B的细绳与直杆成30°角,如图所示,求:
(1)使A、B做匀速圆周运动的向心力各是什么力?各有多大?
(2)若角速度变大将发生什么现象?
4、如图所示,直径为d的纸制圆筒以角速度ω绕垂直于纸面的轴O匀速运动(图示为截面).从枪口发射的子弹沿直径穿过圆筒.若子弹在圆筒旋转不到半周时,在圆周上留下a、b两个弹孔.已知aO与bO夹角为θ,求子弹的速度.若无旋转不到半周的限制,则子弹的速度又如何?
5、(2019 太原五中高三第一次段考)物体做圆周运动时所需的向心力F需由物体运动情况决定,合力提供的向心力F供由物体受力情况决定。若某时刻F需=F供,则物体能做圆周运动;若F需>F供,物体将做离心运动;若F需<F供,物体将做近心运动。现有一根长L=0.5 m的刚性轻绳,其一端固定于O点,另一端系着质量m=1 kg的小球(可视为质点),将小球提至O点正上方的A点处,此时绳刚好伸直且无张力,如图所示。不计空气阻力,g取10 m/s2,则:
(1)在小球以速度v1=5 m/s水平抛出的瞬间,绳中的张力为多少?
(2)在小球以速度v2=1 m/s水平抛出的瞬间,绳中若有张力,求其大小;若无张力,试求轻绳再次伸直时所经历的时间。
6、如图所示为录音机在工作时的示意图,轮子1是主动轮,轮子2为从动轮,轮1和轮2就是磁带盒内的两个转盘,空带一边半径为r1=0.5cm,满带一边半径为r2=3cm,已知主动轮转速不变,恒为n1=36 r/min,试求:
(1)从动轮2的转速变化范围;
(2)磁带运动的速度变化范围.
【答案及解析】
一、选择题:
1、B、C、D
解析:由于a、b两点在同一球上,因此a、b两点的角速度ω相同,选项B正确;而据v=ωr可知,选项A错误;由几何关系有,当θ=30°时,,则,选项C正确;由,可知,选项D正确.
2、D
解析:物体在最低点的向心力是,所以选项A错误;
受到的摩擦力是,所以BC选项都错误;
因为物块受到水平向左的摩擦力和竖直向上的向心力,这两个力的合力就是物块受到的合力,所以合力的方向是斜向左上方,D选项正确。
3、D
解析:对小物体在顶部A处用牛顿第二定律,将代入上式得到,球面对球的支持力F=0,因此,小球在不计空气阻力的情况下,只受重力以水平速度抛出,做平抛运动,所以D选项正确。
4、A
解析:本题属于摩擦传动,摩擦传动的特点是各个轮边缘的线速度大小相等,即v1=v2=v3,即有,显然选项A正确.
5、AC
解析:A、B两个球受到的向心力是一对相互作用力,且相同的时间转过的角度一定相同,所以;由向心力公式可知,它们的轨道半径与其质量成反比,所以一定等于,选项AC正确。只要A、B两个球的轨道半径满足与质量成反比关系,无论角速度多大,两个小球总是保持在原来的轨道上运动,既不离心运动也不会向心运动。
6、C
解析:由图可知,主动轮A匀速转动时,A、B两轮边缘上的点的线速度大小相等,由
由于小木块恰能在A轮边缘上静止,,则由静摩擦力提供的向心力达到最大值 。
设小木块放在B轮上能使木块相对静止的距B转轴的最大距离为r,则向心力由最大静摩擦力提供,故,所以选项C正确。
7、B
解析:球在最高点对杆恰好无压力时,重力提供向心力,根据牛顿第二定律,有:,解得:,由于,故杆对球有支持力,根据牛顿第二定律,有:,解得:,根据牛顿第三定律,球对杆由向下的压力,大小为,故选B。
8、C
解析:绳子拉力时刻与速度方向垂直,只改变速度的方向不改变速度的大小,故小球做匀速圆周运动,故A错误;
,v与L不变,故细线拉力的大小不变,B错误;
小球做匀速圆周运动时,绳子的拉力提供向心力,只要v0>0,小球都能通过A点,故C正确,D错误,故选C。
二、填空题:
1、0,3mg
解析:当球的线速度时,对小球在最高点处用牛顿第二定律:,解得线的拉力是;
当球的线速度时,对小球在最高点处用牛顿第二定律:,解得线的拉力是;
2、 (n=1,2,3,…)
解析:小球做平抛运动,在竖直方向上,则运动时间,则运动时间.
又因为水平位移为R,
所以球的速度.
在时间t内盘转过的角度,
又因为,则转盘角速度
.
3、(1)4.55 (2)1.46
解析:(1)转速,,
由图可知:T=0.22s,.
(2)每个周期内接收到信号的时间,
弧长,,
可得1.46 cm.
三、计算题:
1、(1) 球自由落体运动到桶底的时间t必须是圆周运动周期T的整数倍。
(2)
解析:小球射入桶内的运动可以分解为两个分运动:一个是水平面内的匀速圆周运动,一个是竖直方向上的自由落体运动。要使得小球从B处射出,必须满足的条件是小球落到桶底的这段时间内,水平方向完成了整数个圆周,也就是说,球自由落体运动到桶底的时间t必须是圆周运动周期T的整数倍。
在竖直方向:
在水平方向:
解得小球射入速度是
在水平方向球对桶壁的压力大小等于桶壁对于球的弹力,这个弹力提供向心力使球在水平面内做匀速圆周运动,由牛顿第二定律得
2、解析:(1)飞机从俯冲状态往上拉时,人体处于超重状态,血液因为离心运动而向人体的下部分聚集,心脏不能像平常状态运输血液,导致血压降低。
(2)血液在人体中的作用是:通过血液循环,将从肺部获取的氧气,以及从消化器官获取的营养,运送到人体的各个器官,供给生理活动需要,并带走代谢所产生的废物。
(3)由向心加速度的计算公式可得:
仪器的转速
3、解析:(1)物体A随转台一起做匀速圆周运动,和转台保持相对静止,重力跟支持力平衡,转台对A的静摩擦力就是使A做匀速圆周运动所需向心力,如图所示。
设转动时角速度为, 则有:
①
小球B由绳子拴着随转台转动做匀速圆周运动时,它所需的向心力是它的重力和绳子对它的拉力的合力,即:
②
从②式得:
rad/s
rad/s
所以:
(2)如果角速度增大,则A和B所需的向心力也相应增大。A的向心力是转台对它的静摩擦力,在最大静摩擦力的范围内,物体A仍将随转台转动而做匀速圆周运动。由于,当时,静摩擦力就不足以提供A所需的向心力,物体A就将脱离转台沿切线方向飞出。
当角速增大时,物体B将升高,绳子和直杆间的夹角增大,这样它的重力和绳子对它的拉力的合力也相应增大,以适应所需向心力的增大;角速度愈大,B将升得愈高,张角也愈大。由于B的升高,拉力随之增大,如果越过了绳所能承受的最大拉力,绳将被拉断而B即沿切线方向飞出。
4、 (n=0,1,2,…).
解析:设子弹速度为v,则子弹穿过圆筒的时间.
此时间内圆筒转过的角度.
据,得.
则子弹的速度.
本题中若无旋转不到半圆的限制,则在时间t内转过的角度.
则子弹的速度(n=0,1,2,…).
5、解析:(1)要使小球在竖直面内能够做完整的圆周运动,在最高点时至少应该是重力作为所需要的向心力,所以由得:
因为v1>v0,故绳中有张力,由牛顿第二定律得:
代入数据解得,绳中的张力为:T=40 N
(2)因为v2<v0,故绳中没有张力,小球将做平抛运动,如图所示,
水平方向:x=v2t
竖直方向:
L2=(y-L)2+x2
代入数据解得:t=0.4 s
6、(1)6 r/min~216 r/min(2)0.019 m/s~0.113 m/s
解析:本题应抓住主动轮(r1)的角速度恒定不变这一特征,再根据同一时刻两轮磁带走动的线速度相等,从磁带转动时半径的变化来求解.
(1)因为,且两轮边缘上各点的线速度相等,所以,即.
当r2=3cm时,从动轮2的转速最小,.当磁带走完,即r2=0.5cm,r1=3cm时,从动轮2的转速最大,为,故从动轮2的转速变化范围是6 r/min~216 r/min.
(2)由得知:
cm时,,
cm时,.
故磁带的速度变化范围是0.019 m/s~0.113 m/s.
