人教版八年级数学下册第十九章 一次函数19.2.3 一次函数与方程、不等式课件(共41张)
文档属性
| 名称 | 人教版八年级数学下册第十九章 一次函数19.2.3 一次函数与方程、不等式课件(共41张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-25 23:49:07 | ||
图片预览









文档简介
(共41张PPT)
19.2 一次函数
19.2.3 一次函数与方程、不等式
人教版 数学 八年级 下册
今天数学王国搞了个家庭聚会,各个成员按照自己所在的集合就坐,这时来了“x+y=5”.
二元一次方程
一次函数
x+y=5
到我这里来
到我这里来
导入新知
这是怎么回事? x+y=5应该坐在哪里呢?
1. 认识一次函数与一元(二元)一次方程(组)、一元一次不等式之间的联系.
2. 会用函数观点解释方程和不等式及其解(解集)的意义.
素养目标
3. 经历用函数图象表示方程、不等式解的过程,进一步体会“以形表示数,以数解释形”的数形结合思想.
我们先来看下面两个问题:
(1)解方程2x+20=0.
(2)当自变量x为何值时函数y=2x+20的值为0?
问题:
1. 对于2x+20=0 和y=2x+20,从形式上看,有什么相同和不同?
2. 从问题本质上看,(1)和(2)有什么关系?
探究新知
知识点 1
一次函数与一元一次方程
作出函数y=2x+20的图象.
【思考】函数图象哪一个点的坐标表示函数值为0?
与x轴的交点(-10,0)
即当x=-10时,函数y=2x+20的值为0,这说明方程2x+20=0的解是x=-10.方程的解是函数与x轴的交点的横坐标.
20
-10
0
x
y
问题(1)解方程2x+20=0,
得x=-10.
所对应的( )为何值?
实质上这可以通过解方程2x+20=0,得出x=-10.因此,这两个问题实际上是同一个问题.
问题(2)就是要考虑当函数y=2x+20的值为( )时,
自变量x
0
从图象上看:
探究新知
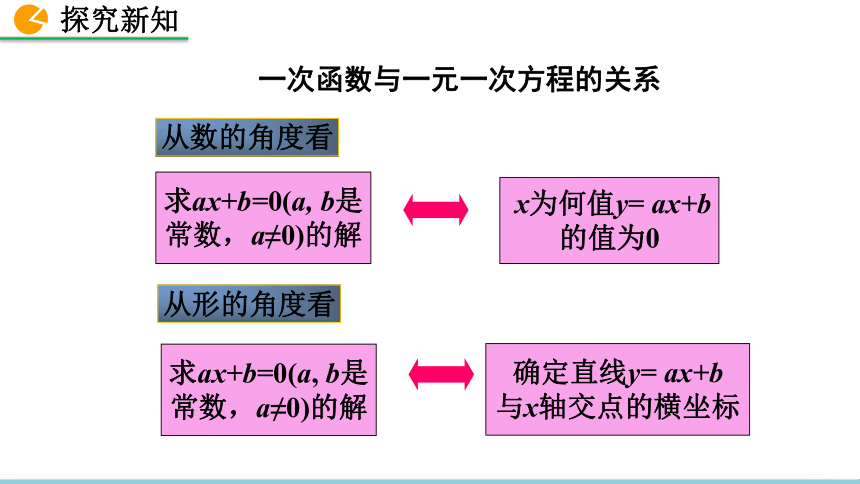
【思考】由上面两个问题的关系,能进一步得到解方程ax+b=0(a, b为常数)与求自变量x为何值时,一次函数y=ax+b的值为0有什么关系?
探究新知
由上面问题可以得到,一元一次方程的求解与解相应的一次函数问题相一致.
由于任何一个一元一次方程都可转化ax+b=0(a,b为常数,
a≠0)的形式,所以解一元一次方程可以转化为:当某个一次函数值y为0时,求相应的自变量x的值.从图象上看,这相当于已知直线y=ax+b,确定它与x轴交点的横坐标的值.
求ax+b=0(a, b是
常数,a≠0)的解
x为何值y= ax+b
的值为0
求ax+b=0(a, b是
常数,a≠0)的解
确定直线y= ax+b
与x轴交点的横坐标
从数的角度看
从形的角度看
探究新知
一次函数与一元一次方程的关系
1.以下的一元一次方程与一次函数问题是同一问题
序号 一元一次方程问题 一次函数问题
1 解方程3x-2=0 当x为何值时,
y=3x-2的值为0
2 解方程8x+3=0
3 当x为何值时,
y= -7x+2的值为0
4 解方程
3x-2=8x+3
当x为何值时,y=8x+3的值为0
解方程-7x+2=0
当x为何值时, y=-5x-5的值为0
巩固练习
例1 一个物体现在的速度是5米/秒,其速度每秒增加2米/秒,再过几秒它的速度为17米/秒?(从方程、函数解析式及图象三个不同方面进行解答)
解法1:设再过x秒它的速度为17米/秒,
由题意得2x+5=17
解得 x=6
答:再过6秒它的速度为17米/秒.
探究新知
素养考点 1
利用一次函数、方程及图象解答问题
解法2:速度y(单位:米/秒)是时间x(单位:秒)的函数y=2x+5
由2x+5=17 得 2x-12=0
由右图看出直线y=2x-12与x轴的交点为(6,0),得x=6.
O
x
y
6
-12
y=2x-12
探究新知
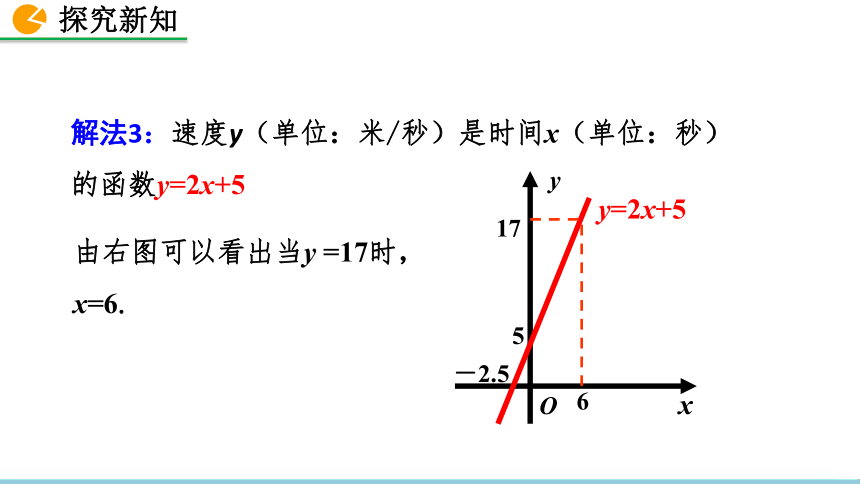
解法3:速度y(单位:米/秒)是时间x(单位:秒)的函数y=2x+5
由右图可以看出当y =17时,x=6.
y=2x+5
x
y
O
6
17
5
-2.5
探究新知
2.当自变量x的取值满足什么条件时,函数y=2x+8的值满足下列条件?(1)y=0;(2)y=-8.
3.已知方程ax+b=0的解是-2,下列图象一定不是直线y=ax+b的是( )
0
x
y
0
x
y
0
x
y
0
x
y
-2
-2
-2
-2
-2
A
B
C
D
B
x=-4;
x=-8.
巩固练习
解:
【讨论】观察下面3个不等式有什么共同点与不同点?
(1)
>2;
(2)
<0;
(3)
<-1
3个不等式相同的特点是:不等号左边都是 ;
不同点是:不等号及不等号右边分别是 , , .
2
0
-1
探究新知
知识点 2
一次函数与一元一次不等式
【讨论】你能从函数的角度对以上3个不等式进行解释吗?
的函数值分别为 、
、 时,求
自变量x的取值范围
解释1:这3个不等式相当于在一次函数
小于-1
大于2
小于0
探究新知
解释2:在直线
上取纵坐标分别.
满足条件 、 、 的点,看他们的横坐标分别满足什么条件.
大于2
小于0
小于-1
探究新知
探究新知
归纳总结
因为任何一个以x为未知数的一元一次不等式都可以变形为ax +b>0或ax +b<0(a≠0)的形式,所以解一元一次不等式相当于在某个一次函数y=ax +b的值 或 时,求自变量x的 .
取值范围
大于0
小于0
求kx+b>0(或<0)
(k≠0)的解集
y=kx+b的值
大于(或小于)0时,
x的取值范围
从“函数值”看
求kx+b>0(或<0)
(k≠0)的解集
确定直线y=kx+b
在x轴上方(或下方)
的图象所对应的x
取值范围
从“函数图象”看
一次函数与一元一次不等式的关系
探究新知
4.已知函数y=x-3,当x 时, y>0;
当x 时, y<0.
> 3
< 3
5.已知一次函数y=kx+b的图象如图所示,则不等式kx+b>0的解集是( )
A.x>-2? B.x<-2
C.x>-1???? D.x<-1
B
巩固练习
-2
-1
x
y
0
y=kx+b
例2 画出函数y=-3x+6的图象,结合图象求:
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当x取何值时,y<3?
解:作出函数y=-3x+6的图象,如图所示,图象与x轴交于点B(2,0).
x
O
B(2,0)
A(0,6)
y
探究新知
素养考点 1
利用一次函数的图象解一元一次不等式
解:(1)由图象可知,
不等式-3x+6>0 的解集是图象位于
x轴上方的x的取值范围,即x<2;
不等式 -3x+6<0的解集是图象位于 x轴下方的x的取值范围,即x>2;
x
O
B(2,0)
A(0,6)
3
1
(1,3)
y
(2)由图象可知,当x>1时,y<3.
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当x取何值时,y<3?
探究新知
6.如图,已知直线y=kx+b与x轴交于点(- 4,0),则当y>0时,
x的取值范围是( )
A.x>-4
B. x>0
C. x<-4
D. x<0
C
巩固练习
y
y=kx+b
x
1号探测气球从海拔5 m 处出发,以1 m/min 的速度上升.与此同时,2 号探测气球从海拔15 m 处出发,以0.5 m/min 的速度上升.两个气球都上升了1 h.
(1)请用解析式分别表示两个气
球所在位置的海拔 y(m)与气球
上升时间 x(min)的函数关系.
h1
h2
气球1 海拔高度:y =x+5;
气球2 海拔高度:y =0.5x+15.
探究新知
解:
知识点 3
一次函数与二元一次方程组
【讨论】一次函数与二元一次方程有什么关系?
一次函数
二元一次方程
一次函数
y =0.5x+15
二元一次方程
y -0.5x =15
二元一次方程
y =0.5x+15
用方程观点看
用函数观点看
从式子(数)角度看:
探究新知
由函数图象的定义可知:
直线y =0.5x+15上的每个点的坐标(x,y)都能使等式y=0.5x+15成立,即直线y =0.5x+15上的每个点的坐标都是二元一次方程y=0.5x+15的解.
【讨论】从形的角度看,一次函数与二元一次方程有什么关系?
15
10
5
-5
5
10
O
x
y
y =0.5x+15
探究新知
从数的角度看:
就是求自变量为何值时,两个一次函数 y =x+5,y =0.5x+15 的函数值相等,并求出函数值.
解方程组
y =x+5
y =0.5x+15
h1
h2
(2)什么时刻,1 号气球的高度赶上2 号气球的高度?这时的高度是多少?请从数和形两方面分别加以研究.
气球1 海拔高度:y =x+5
气球2 海拔高度:y =0.5x+15
探究新知
二元一次方程
组的解就是相应的
两个一次函数图象
的交点坐标.
A(20,25)
30
25
20
15
10
5
10
20
y =x+5
y =0.5x+15
15
5
O
x
y
从形的角度看,二元一次方程组与一次函数有什么关系?
探究新知
探究新知
归纳总结
一般地,任何一个二元一次方程都可以转化为一次函数y=kx+b(k、b为常数,且k≠0)的形式,所以每个二元一次方程都对应一个一次函数,也对应一条直线.
方程组的解 对应两条直线交点的坐标.
观察函数图象,直接回答下列问题:
(1)在什么时候,1 号气球比2 号气球高?
(2)在什么时候,2 号气球比1 号气球高?
气球1 海拔高度:y =x+5
气球2 海拔高度:y =0.5x+15
(1)20min后,1 号气球比2 号气球高.
(2)0~20min时,2 号气球比1 号气球高.
探究新知
例3 如图,求直线l1与l2 的交点坐标.
分析:由函数图象可以求直线l1与l2的解析式,进而通过方程组求出交点坐标.
探究新知
素养考点 1
利用一次函数的图象解二元一次方程组
解方程组
y =2x+2,
y =-x+3,
解:因为直线l1过点(-1,0),
(0,2) ,用待定系数法可求得
直线l1的解析式为y =2x+2.同理
可求得直线l2的解析式为y =-x+3.
得
即直线l1与l2 的交点坐标为
探究新知
7.如图,一次函数y=ax+b与y=cx+d的图象交于点P,则方程组 的解是多少?
解:此方程组的解是
1
2
3
-1
-2
-3
-1
-3
-4
-5
2
O
-2
1
4
-6
x
y
P
y=ax+b
y=cx+d
巩固练习
1.(2018?呼和浩特)若以二元一次方程x+2y﹣b=0的解为坐标的点(x,y)都在直线 上,则常数b=( )
A. B.2 C.﹣1 D.1
巩固练习
连接中考
B
2.(2019?遵义)如图所示,直线l1: 与直线l2: 交于点P(﹣2,3),不等式 的解集是( )
A.x>﹣2 B.x≥﹣2
C.x<﹣2 D.x≤﹣2
A
1.直线 与x轴的交点是(? )
A.(0,-3)??? B.(-3,0)????
C.(0,3)??? D.(0,-3)
2.方程 的解是 ,则函数 在自变量x等于 时的函数值是8.
B
x=2
2
基础巩固题
课堂检测
3. 直线 在坐标系中的位置如图,则方程 的解是x=___.
-2
2
x
y
0
-2
课堂检测
基础巩固题
0
4.根据图象,你能直接说出一元一次方程 的解吗?
解:由图象可知x+3=0的
解为x= ?3.
3
x
y
0
-3
从“形”上看
直线y=x+3的图象与x轴交点坐标为(-3,0),这说明方程x+3=0的解是x=-3.
课堂检测
基础巩固题
0
5.当自变量取何值时,函数 与
的值相等?这个函数值是多少?
解: 由已知可得:
2.5x+ 1 = 5x+ 17,
解得:x=-6.4
y=5 ×(- 6.4 )+ 17
y=-15
课堂检测
基础巩固题
6.用函数图象来解决5x+6>3x+10.
解:化简,得2x-4>0.画出直线y=2x-4的图象.
-4
2
y
x
0
y=2x-4
可以看出,当x>2时,这条直线上的点在x轴的上方,即这时y=2x-4>0.
所以不等式的解集是x>2.
课堂检测
基础巩固题
一次函数y1=4x+5与y2=3x+10的图象如图所示,则4x+5>3x+10的解集是( )
A.x<5
B.x>5
C.x>-5
D.x>25
1
B
课堂检测
能力提升题
y=4x+5
y=3x+10
x
y
直线 与x轴的交点的横坐标的值是方程 的解,求a的值.
解:由题意可得:
当直线y=3x+ 6与x轴相交时,y=0
则3x+ 6=0, 解得:x= -2,
当x= -2 时,
2 × (-2) + a =0
解得:a = 4
课堂检测
拓广探索题
一次函数与方程、不等式
解一元一次方程 对应一次函数的值为0时,求相应的自变量的值,即一次函数与x轴交点的横坐标.
解一元一次不等式 对应一次函数的函数值大(小)于0时,求自变量的取值范围,即在x轴上方(或下方)的图象所对应的x取值范围 .
解二元一次方程组 求对应两条直线交点的坐标 .
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
19.2 一次函数
19.2.3 一次函数与方程、不等式
人教版 数学 八年级 下册
今天数学王国搞了个家庭聚会,各个成员按照自己所在的集合就坐,这时来了“x+y=5”.
二元一次方程
一次函数
x+y=5
到我这里来
到我这里来
导入新知
这是怎么回事? x+y=5应该坐在哪里呢?
1. 认识一次函数与一元(二元)一次方程(组)、一元一次不等式之间的联系.
2. 会用函数观点解释方程和不等式及其解(解集)的意义.
素养目标
3. 经历用函数图象表示方程、不等式解的过程,进一步体会“以形表示数,以数解释形”的数形结合思想.
我们先来看下面两个问题:
(1)解方程2x+20=0.
(2)当自变量x为何值时函数y=2x+20的值为0?
问题:
1. 对于2x+20=0 和y=2x+20,从形式上看,有什么相同和不同?
2. 从问题本质上看,(1)和(2)有什么关系?
探究新知
知识点 1
一次函数与一元一次方程
作出函数y=2x+20的图象.
【思考】函数图象哪一个点的坐标表示函数值为0?
与x轴的交点(-10,0)
即当x=-10时,函数y=2x+20的值为0,这说明方程2x+20=0的解是x=-10.方程的解是函数与x轴的交点的横坐标.
20
-10
0
x
y
问题(1)解方程2x+20=0,
得x=-10.
所对应的( )为何值?
实质上这可以通过解方程2x+20=0,得出x=-10.因此,这两个问题实际上是同一个问题.
问题(2)就是要考虑当函数y=2x+20的值为( )时,
自变量x
0
从图象上看:
探究新知
【思考】由上面两个问题的关系,能进一步得到解方程ax+b=0(a, b为常数)与求自变量x为何值时,一次函数y=ax+b的值为0有什么关系?
探究新知
由上面问题可以得到,一元一次方程的求解与解相应的一次函数问题相一致.
由于任何一个一元一次方程都可转化ax+b=0(a,b为常数,
a≠0)的形式,所以解一元一次方程可以转化为:当某个一次函数值y为0时,求相应的自变量x的值.从图象上看,这相当于已知直线y=ax+b,确定它与x轴交点的横坐标的值.
求ax+b=0(a, b是
常数,a≠0)的解
x为何值y= ax+b
的值为0
求ax+b=0(a, b是
常数,a≠0)的解
确定直线y= ax+b
与x轴交点的横坐标
从数的角度看
从形的角度看
探究新知
一次函数与一元一次方程的关系
1.以下的一元一次方程与一次函数问题是同一问题
序号 一元一次方程问题 一次函数问题
1 解方程3x-2=0 当x为何值时,
y=3x-2的值为0
2 解方程8x+3=0
3 当x为何值时,
y= -7x+2的值为0
4 解方程
3x-2=8x+3
当x为何值时,y=8x+3的值为0
解方程-7x+2=0
当x为何值时, y=-5x-5的值为0
巩固练习
例1 一个物体现在的速度是5米/秒,其速度每秒增加2米/秒,再过几秒它的速度为17米/秒?(从方程、函数解析式及图象三个不同方面进行解答)
解法1:设再过x秒它的速度为17米/秒,
由题意得2x+5=17
解得 x=6
答:再过6秒它的速度为17米/秒.
探究新知
素养考点 1
利用一次函数、方程及图象解答问题
解法2:速度y(单位:米/秒)是时间x(单位:秒)的函数y=2x+5
由2x+5=17 得 2x-12=0
由右图看出直线y=2x-12与x轴的交点为(6,0),得x=6.
O
x
y
6
-12
y=2x-12
探究新知
解法3:速度y(单位:米/秒)是时间x(单位:秒)的函数y=2x+5
由右图可以看出当y =17时,x=6.
y=2x+5
x
y
O
6
17
5
-2.5
探究新知
2.当自变量x的取值满足什么条件时,函数y=2x+8的值满足下列条件?(1)y=0;(2)y=-8.
3.已知方程ax+b=0的解是-2,下列图象一定不是直线y=ax+b的是( )
0
x
y
0
x
y
0
x
y
0
x
y
-2
-2
-2
-2
-2
A
B
C
D
B
x=-4;
x=-8.
巩固练习
解:
【讨论】观察下面3个不等式有什么共同点与不同点?
(1)
>2;
(2)
<0;
(3)
<-1
3个不等式相同的特点是:不等号左边都是 ;
不同点是:不等号及不等号右边分别是 , , .
2
0
-1
探究新知
知识点 2
一次函数与一元一次不等式
【讨论】你能从函数的角度对以上3个不等式进行解释吗?
的函数值分别为 、
、 时,求
自变量x的取值范围
解释1:这3个不等式相当于在一次函数
小于-1
大于2
小于0
探究新知
解释2:在直线
上取纵坐标分别.
满足条件 、 、 的点,看他们的横坐标分别满足什么条件.
大于2
小于0
小于-1
探究新知
探究新知
归纳总结
因为任何一个以x为未知数的一元一次不等式都可以变形为ax +b>0或ax +b<0(a≠0)的形式,所以解一元一次不等式相当于在某个一次函数y=ax +b的值 或 时,求自变量x的 .
取值范围
大于0
小于0
求kx+b>0(或<0)
(k≠0)的解集
y=kx+b的值
大于(或小于)0时,
x的取值范围
从“函数值”看
求kx+b>0(或<0)
(k≠0)的解集
确定直线y=kx+b
在x轴上方(或下方)
的图象所对应的x
取值范围
从“函数图象”看
一次函数与一元一次不等式的关系
探究新知
4.已知函数y=x-3,当x 时, y>0;
当x 时, y<0.
> 3
< 3
5.已知一次函数y=kx+b的图象如图所示,则不等式kx+b>0的解集是( )
A.x>-2? B.x<-2
C.x>-1???? D.x<-1
B
巩固练习
-2
-1
x
y
0
y=kx+b
例2 画出函数y=-3x+6的图象,结合图象求:
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当x取何值时,y<3?
解:作出函数y=-3x+6的图象,如图所示,图象与x轴交于点B(2,0).
x
O
B(2,0)
A(0,6)
y
探究新知
素养考点 1
利用一次函数的图象解一元一次不等式
解:(1)由图象可知,
不等式-3x+6>0 的解集是图象位于
x轴上方的x的取值范围,即x<2;
不等式 -3x+6<0的解集是图象位于 x轴下方的x的取值范围,即x>2;
x
O
B(2,0)
A(0,6)
3
1
(1,3)
y
(2)由图象可知,当x>1时,y<3.
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当x取何值时,y<3?
探究新知
6.如图,已知直线y=kx+b与x轴交于点(- 4,0),则当y>0时,
x的取值范围是( )
A.x>-4
B. x>0
C. x<-4
D. x<0
C
巩固练习
y
y=kx+b
x
1号探测气球从海拔5 m 处出发,以1 m/min 的速度上升.与此同时,2 号探测气球从海拔15 m 处出发,以0.5 m/min 的速度上升.两个气球都上升了1 h.
(1)请用解析式分别表示两个气
球所在位置的海拔 y(m)与气球
上升时间 x(min)的函数关系.
h1
h2
气球1 海拔高度:y =x+5;
气球2 海拔高度:y =0.5x+15.
探究新知
解:
知识点 3
一次函数与二元一次方程组
【讨论】一次函数与二元一次方程有什么关系?
一次函数
二元一次方程
一次函数
y =0.5x+15
二元一次方程
y -0.5x =15
二元一次方程
y =0.5x+15
用方程观点看
用函数观点看
从式子(数)角度看:
探究新知
由函数图象的定义可知:
直线y =0.5x+15上的每个点的坐标(x,y)都能使等式y=0.5x+15成立,即直线y =0.5x+15上的每个点的坐标都是二元一次方程y=0.5x+15的解.
【讨论】从形的角度看,一次函数与二元一次方程有什么关系?
15
10
5
-5
5
10
O
x
y
y =0.5x+15
探究新知
从数的角度看:
就是求自变量为何值时,两个一次函数 y =x+5,y =0.5x+15 的函数值相等,并求出函数值.
解方程组
y =x+5
y =0.5x+15
h1
h2
(2)什么时刻,1 号气球的高度赶上2 号气球的高度?这时的高度是多少?请从数和形两方面分别加以研究.
气球1 海拔高度:y =x+5
气球2 海拔高度:y =0.5x+15
探究新知
二元一次方程
组的解就是相应的
两个一次函数图象
的交点坐标.
A(20,25)
30
25
20
15
10
5
10
20
y =x+5
y =0.5x+15
15
5
O
x
y
从形的角度看,二元一次方程组与一次函数有什么关系?
探究新知
探究新知
归纳总结
一般地,任何一个二元一次方程都可以转化为一次函数y=kx+b(k、b为常数,且k≠0)的形式,所以每个二元一次方程都对应一个一次函数,也对应一条直线.
方程组的解 对应两条直线交点的坐标.
观察函数图象,直接回答下列问题:
(1)在什么时候,1 号气球比2 号气球高?
(2)在什么时候,2 号气球比1 号气球高?
气球1 海拔高度:y =x+5
气球2 海拔高度:y =0.5x+15
(1)20min后,1 号气球比2 号气球高.
(2)0~20min时,2 号气球比1 号气球高.
探究新知
例3 如图,求直线l1与l2 的交点坐标.
分析:由函数图象可以求直线l1与l2的解析式,进而通过方程组求出交点坐标.
探究新知
素养考点 1
利用一次函数的图象解二元一次方程组
解方程组
y =2x+2,
y =-x+3,
解:因为直线l1过点(-1,0),
(0,2) ,用待定系数法可求得
直线l1的解析式为y =2x+2.同理
可求得直线l2的解析式为y =-x+3.
得
即直线l1与l2 的交点坐标为
探究新知
7.如图,一次函数y=ax+b与y=cx+d的图象交于点P,则方程组 的解是多少?
解:此方程组的解是
1
2
3
-1
-2
-3
-1
-3
-4
-5
2
O
-2
1
4
-6
x
y
P
y=ax+b
y=cx+d
巩固练习
1.(2018?呼和浩特)若以二元一次方程x+2y﹣b=0的解为坐标的点(x,y)都在直线 上,则常数b=( )
A. B.2 C.﹣1 D.1
巩固练习
连接中考
B
2.(2019?遵义)如图所示,直线l1: 与直线l2: 交于点P(﹣2,3),不等式 的解集是( )
A.x>﹣2 B.x≥﹣2
C.x<﹣2 D.x≤﹣2
A
1.直线 与x轴的交点是(? )
A.(0,-3)??? B.(-3,0)????
C.(0,3)??? D.(0,-3)
2.方程 的解是 ,则函数 在自变量x等于 时的函数值是8.
B
x=2
2
基础巩固题
课堂检测
3. 直线 在坐标系中的位置如图,则方程 的解是x=___.
-2
2
x
y
0
-2
课堂检测
基础巩固题
0
4.根据图象,你能直接说出一元一次方程 的解吗?
解:由图象可知x+3=0的
解为x= ?3.
3
x
y
0
-3
从“形”上看
直线y=x+3的图象与x轴交点坐标为(-3,0),这说明方程x+3=0的解是x=-3.
课堂检测
基础巩固题
0
5.当自变量取何值时,函数 与
的值相等?这个函数值是多少?
解: 由已知可得:
2.5x+ 1 = 5x+ 17,
解得:x=-6.4
y=5 ×(- 6.4 )+ 17
y=-15
课堂检测
基础巩固题
6.用函数图象来解决5x+6>3x+10.
解:化简,得2x-4>0.画出直线y=2x-4的图象.
-4
2
y
x
0
y=2x-4
可以看出,当x>2时,这条直线上的点在x轴的上方,即这时y=2x-4>0.
所以不等式的解集是x>2.
课堂检测
基础巩固题
一次函数y1=4x+5与y2=3x+10的图象如图所示,则4x+5>3x+10的解集是( )
A.x<5
B.x>5
C.x>-5
D.x>25
1
B
课堂检测
能力提升题
y=4x+5
y=3x+10
x
y
直线 与x轴的交点的横坐标的值是方程 的解,求a的值.
解:由题意可得:
当直线y=3x+ 6与x轴相交时,y=0
则3x+ 6=0, 解得:x= -2,
当x= -2 时,
2 × (-2) + a =0
解得:a = 4
课堂检测
拓广探索题
一次函数与方程、不等式
解一元一次方程 对应一次函数的值为0时,求相应的自变量的值,即一次函数与x轴交点的横坐标.
解一元一次不等式 对应一次函数的函数值大(小)于0时,求自变量的取值范围,即在x轴上方(或下方)的图象所对应的x取值范围 .
解二元一次方程组 求对应两条直线交点的坐标 .
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
