初中数学沪科版九年级下册第二学期期末测试(含答案)
文档属性
| 名称 | 初中数学沪科版九年级下册第二学期期末测试(含答案) | 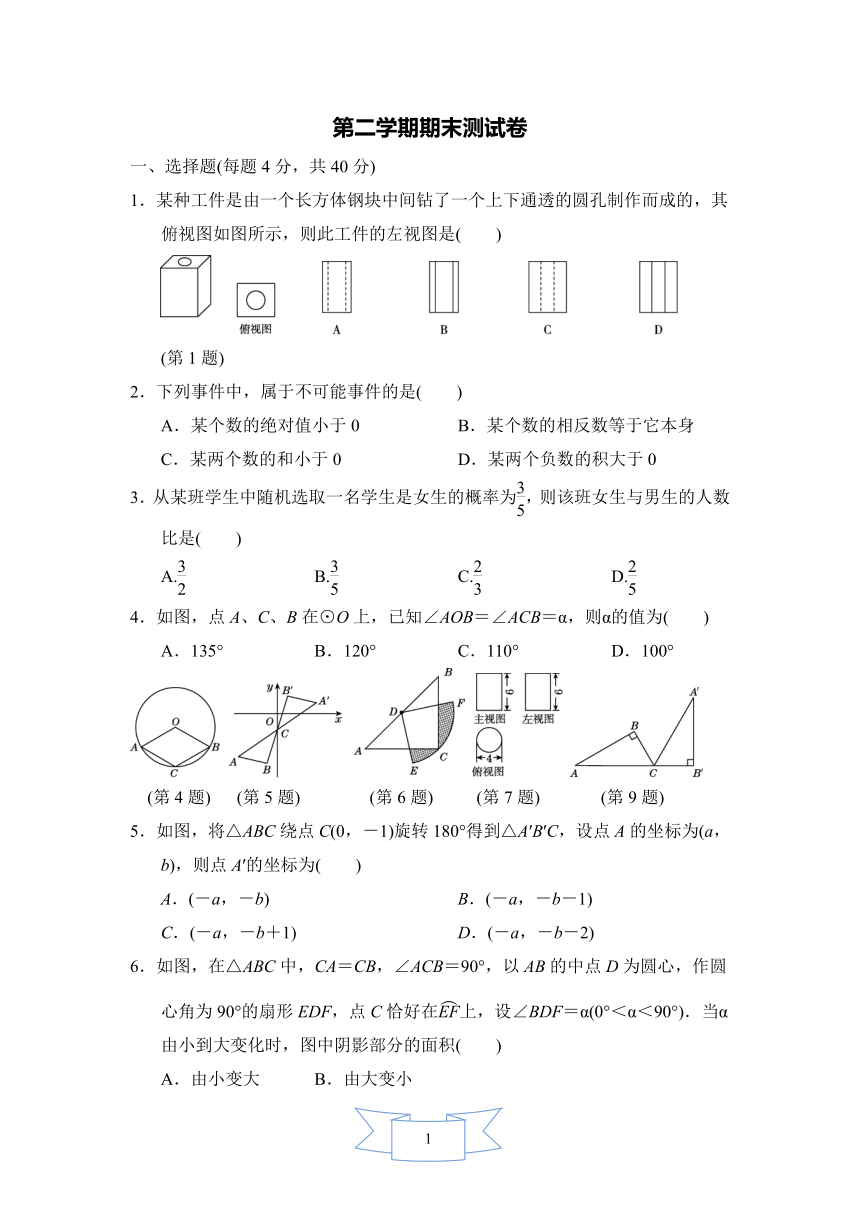 | |
| 格式 | zip | ||
| 文件大小 | 184.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 08:59:16 | ||
图片预览




文档简介
第二学期期末测试卷
一、选择题(每题4分,共40分)
1.某种工件是由一个长方体钢块中间钻了一个上下通透的圆孔制作而成的,其俯视图如图所示,则此工件的左视图是( )
(第1题)
2.下列事件中,属于不可能事件的是( )
A.某个数的绝对值小于0 B.某个数的相反数等于它本身
C.某两个数的和小于0 D.某两个负数的积大于0
3.从某班学生中随机选取一名学生是女生的概率为,则该班女生与男生的人数比是( )
A. B. C. D.
4.如图,点A、C、B在⊙O上,已知∠AOB=∠ACB=α,则α的值为( )
A.135° B.120° C.110° D.100°
(第4题) (第5题) (第6题) (第7题) (第9题)
5.如图,将△ABC绕点C(0,-1)旋转180°得到△A′B′C,设点A的坐标为(a,b),则点A′的坐标为( )
A.(-a,-b) B.(-a,-b-1)
C.(-a,-b+1) D.(-a,-b-2)
6.如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形EDF,点C恰好在上,设∠BDF=α(0°<α<90°).当α由小到大变化时,图中阴影部分的面积( )
A.由小变大 B.由大变小
C.不变 D.先由小变大,后由大变小
7.一个几何体的三视图如图所示,那么这个几何体的侧面积是( )
A.16π B.24π C.32π D.48π
8.已知圆锥的底面半径为4 cm,母线长为6 cm,则它的侧面展开图的面积等于( )
A.24 cm2 B.48 cm2 C.24π cm2 D.12π cm2
9.如图,已知在Rt△ABC中,∠ABC=90°,∠BAC=30°,AB=2 cm,将△ABC绕顶点C顺时针旋转至△A′B′C的位置,且A,C,B′三点在同一条直线上,则点A经过的路线的长度是( )
A.8 cm B.4 cm C.π cm D.π cm
10.如图,已知⊙O的半径为1,锐角三角形ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
A.OM的长 B.2OM的长 C.CD的长 D.2CD的长
(第10题) (第11题) (第13题) (第14题)
二、填空题(每题5分,共20分)
11.如图,点A、B把⊙O分成2∶7两条弧,则∠AOB=________.
12.箱子里放有2个黑球和2个红球,它们除颜色外其余都相同,现从箱子里随机摸出2个球,恰好为1个黑球和1个红球的概率是________.
13.如图,四边形ABCD为⊙O的内接四边形,已知∠C=∠D,则AB与CD的位置关系是________.
14.如图,△ABC内接于⊙O,AB是⊙O的直径,直线AE是⊙O的切线,CD平分∠ACB,若∠CAE=21°,则∠BFC的度数为________.
三、(每题8分,共16分)
15.我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段AB的最小覆盖圆就是以线段AB为直径的圆.
(1)如图,请分别作出两个三角形的最小覆盖圆;(要求:尺规作图,保留作图痕迹,不写作法)
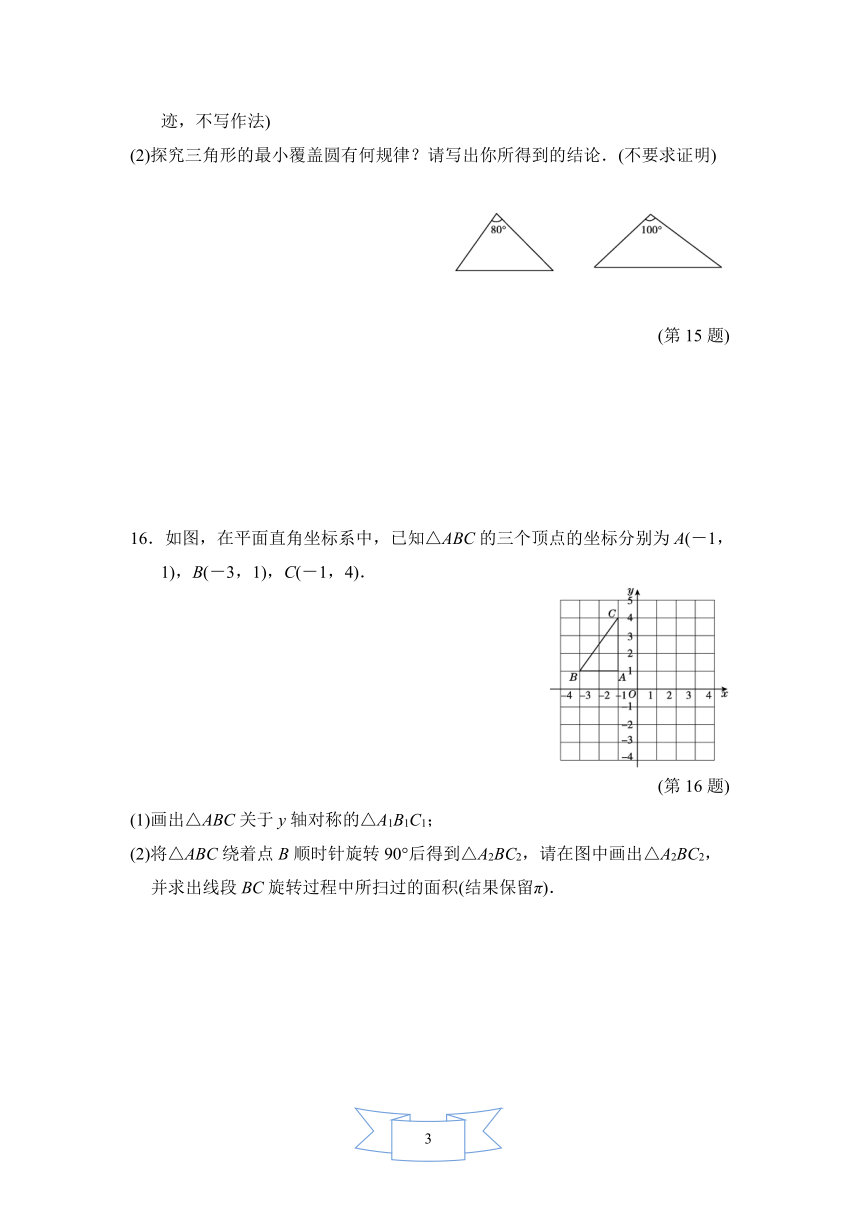
(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论.(不要求证明)
(第15题)
16.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-1,1),B(-3,1),C(-1,4).
(第16题)
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC绕着点B顺时针旋转90°后得到△A2BC2,请在图中画出△A2BC2,并求出线段BC旋转过程中所扫过的面积(结果保留π).
四、(每题8分,共16分)
17.如图,在一个宁静的夜晚,月光明亮,张芳和身高为1.6 m的李红在人民广场上玩,张芳测得李红的影长AB为1 m,并立刻测得小树的影长CD为1.5 m,请你算一下小树的高度.
(第17题)
18.一个不透明的袋中装有20个只有颜色不同的球,其中有5个黄球,8个黑球,7个红球.
(1)求从袋中摸出1个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀袋中的球,使从袋中摸出1个球是黑球的概率是.求从袋中取出黑球的个数.
五、(每题10分,共20分)
19.一个几何体的三视图如图所示,它的俯视图为菱形,请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.
(第19题)
20.在不透明的袋中有大小、形状和质地等完全相同的小球,它们分别标有数字-1、-2、1、2,从袋中任意摸出一个小球(不放回),将袋中剩余的小球搅匀后,再从袋中摸出另一个小球.
(1)请你表示摸出小球上的数字可能出现的所有结果;
(2)规定:如果摸出的两个小球上的数字都是方程x2-3x+2=0的根,则小明赢.如果摸出的两个小球上的数字都不是方程x2-3x+2=0的根,则小亮赢.你认为这个游戏规则对小明、小亮双方公平吗?请说明理由.
六、(12分)
21.如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4.
(第21题)
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
七、(12分)
22.如图,图①是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图②.已知铁环的半径为5个单位(每个单位为5 cm),设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=.
(1)求点M离地面AC的高度BM(单位:cm);
(2)设人站立点C与点A的水平距离AC等于11个单位,求铁环钩MF的长度(单位:cm).
(第22题)
八、(14分)
23.如图,△ABC为⊙O的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD交AD于E,交AB于F,交⊙O于G.
(1)请判断直线PA与⊙O的位置关系,并说明理由;
(2)求证:AG2=AF·AB;
(3)若⊙O的直径为10,AC=2,AB=4,求△AFG的面积.
(第23题)
答案
一、1.A
2.A 点拨:任意实数的绝对值都大于或等于0.
3.A 4.B 5.D 6.C
7.B 点拨:由三视图知该几何体是圆柱,其底面直径是4,高是6,故这个几何体的侧面积是π×4×6=24π.
8.C 9.D
10.A 点拨:如图,连接OA,OB.∵OA=OB,OM⊥AB,∴∠BOM=∠AOM=∠AOB.∵∠C=∠AOB,
∴∠BOM=∠C.∵BD⊥AC,OM⊥AB,
∴∠CBD+∠C=90°,∠OBM+∠BOM=90°,∴∠CBD=∠OBM.
∵sin∠OBM==OM,
∴sin∠CBD=OM,即sin∠CBD的值等于OM的长.
(第10题)
二、11.80° 12.
13.AB∥CD 14.114°
三、15.解:(1)如图所示.
(第15题)
(2)若三角形为锐角三角形,则其最小覆盖圆为三角形的外接圆;若三角形为直角三角形或钝角三角形,则其最小覆盖圆是以三角形最长边(直角或钝角所对的边)为直径的圆.
16.解:(1)△A1B1C1如图所示.
(2)△A2BC2如图所示.
线段BC旋转过程中所扫过的面积S==.
(第16题)
四、17.解:由题意得=,
即=,
∴CF=1.6×1.5=2.4(m),
即小树的高度为2.4 m.
18.解:(1)20个球里面有5个黄球,故P(摸出1个球是黄球)==.
(2)设从袋中取出x(0因为从袋中摸出1个球是黑球的概率是,
所以=,解得x=2.
经检验,x=2是所列方程的解,且符合实际.所以从袋中取出了2个黑球.
五、19.解:该几何体的形状是直四棱柱.
由三视图知,棱柱底面菱形的对角线长分别为4 cm,3 cm.
∴菱形的边长为 cm,
∴棱柱的侧面积S=×8×4=80(cm2).
20.解:(1)可能出现的所有结果如下表:
-1
-2
1
2
-1
——
(-1,-2)
(-1,1)
(-1,2)
-2
(-2,-1)
——
(-2,1)
(-2,2)
1
(1,-1)
(1,-2)
——
(1,2)
2
(2,-1)
(2,-2)
(2,1)
——
(2)∵x2-3x+2=0,
∴(x-1)(x-2)=0,
∴x1=1,x2=2.
∵共有12种等可能的结果,其中摸出的两个小球上的数字都是方程x2-3x+2=0的根的结果一共有2种,摸出的两个小球上的数字都不是方程的根的结果一共有2种,
∴P(小明赢)=,P(小亮赢)=,
∴游戏规则公平.
六、21.(1)证明:∵AB=AC,
∴∠ABE=∠C.
∵=,∴∠C=∠D.
∴∠ABE=∠D.
又∵∠BAE=∠DAB,
∴△ABE∽△ADB.
(2)解:∵△ABE∽△ADB,
∴=.
∴AB2=AD·AE=(AE+ED)·AE=(2+4)×2=12.∴AB=2.
(3)解:直线FA与⊙O相切.理由如下:
连接OA.∵BD为⊙O的直径,
∴∠BAD=90°.
∴BD===4.
∴BF=BO=BD=2.
又∵AB=2,∴BF=BO=AB.
∴∠F=∠BAF,∠BOA=∠BAO.
∴∠OAF=90°.
又OA为半径,∴直线FA与⊙O相切.
七、22.解:过M作与AC平行的直线,与OA、FC分别相交于H、N,如图.
(1)在Rt△OHM中,∠OHM=90°,OM=5,
所以HM=OM·sinα=3,
所以OH=4,
所以MB=HA=5-4=1,
1×5=5(cm),
所以点M离地面AC的高度BM为5 cm.
(2)易知HN⊥FC,HM⊥OA,∠OMF=90°,所以∠MOH+∠OMH=∠OMH+∠FMN=90°,
所以∠FMN=∠MOH=α,
所以sinα==.
即得FN=FM,
又由(1)知AB=HM=3.
在Rt△FMN中,∠FNM=90°,
易知MN=BC=AC-AB=11-3=8.
由勾股定理得FM2=FN2+MN2,
即FM2=+82,
解得FM=10,
10×5=50(cm),
所以铁环钩MF的长度为50 cm.
(第22题)
八、23.(1)解:PA与⊙O相切.
理由如下:连接CD.
∵AD为⊙O的直径,∴∠ACD=90°.
∴∠D+∠CAD=90°.
∵∠B=∠D,∠PAC=∠B,∴∠PAC=∠D.
∴∠PAC+∠CAD=90°,即DA⊥PA.
∵AD是⊙O的直径,∴PA与⊙O相切.
(2)证明:连接BG.
∵AD为⊙O的直径,CG⊥AD,∴=.
∴∠AGF=∠ABG.
∵∠GAF=∠BAG,∴△AGF∽△ABG.
∴AG∶AB=AF∶AG. ∴AG2=AF·AB.
(3)解:连接BD.
∵AD是⊙O的直径,∴∠ABD=90°.
∵AG2=AF·AB,AG=AC=2,AB=4,∴AF==.
∵CG⊥AD,∴∠AEF=∠ABD=90°.
又∵∠EAF=∠BAD,∴△AEF∽△ABD.
∴=,即=,解得AE=2.
∴EF==1.
∵EG==4,
∴FG=EG-EF=4-1=3.
∴S△AFG=FG·AE=×3×2=3.
一、选择题(每题4分,共40分)
1.某种工件是由一个长方体钢块中间钻了一个上下通透的圆孔制作而成的,其俯视图如图所示,则此工件的左视图是( )
(第1题)
2.下列事件中,属于不可能事件的是( )
A.某个数的绝对值小于0 B.某个数的相反数等于它本身
C.某两个数的和小于0 D.某两个负数的积大于0
3.从某班学生中随机选取一名学生是女生的概率为,则该班女生与男生的人数比是( )
A. B. C. D.
4.如图,点A、C、B在⊙O上,已知∠AOB=∠ACB=α,则α的值为( )
A.135° B.120° C.110° D.100°
(第4题) (第5题) (第6题) (第7题) (第9题)
5.如图,将△ABC绕点C(0,-1)旋转180°得到△A′B′C,设点A的坐标为(a,b),则点A′的坐标为( )
A.(-a,-b) B.(-a,-b-1)
C.(-a,-b+1) D.(-a,-b-2)
6.如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形EDF,点C恰好在上,设∠BDF=α(0°<α<90°).当α由小到大变化时,图中阴影部分的面积( )
A.由小变大 B.由大变小
C.不变 D.先由小变大,后由大变小
7.一个几何体的三视图如图所示,那么这个几何体的侧面积是( )
A.16π B.24π C.32π D.48π
8.已知圆锥的底面半径为4 cm,母线长为6 cm,则它的侧面展开图的面积等于( )
A.24 cm2 B.48 cm2 C.24π cm2 D.12π cm2
9.如图,已知在Rt△ABC中,∠ABC=90°,∠BAC=30°,AB=2 cm,将△ABC绕顶点C顺时针旋转至△A′B′C的位置,且A,C,B′三点在同一条直线上,则点A经过的路线的长度是( )
A.8 cm B.4 cm C.π cm D.π cm
10.如图,已知⊙O的半径为1,锐角三角形ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
A.OM的长 B.2OM的长 C.CD的长 D.2CD的长
(第10题) (第11题) (第13题) (第14题)
二、填空题(每题5分,共20分)
11.如图,点A、B把⊙O分成2∶7两条弧,则∠AOB=________.
12.箱子里放有2个黑球和2个红球,它们除颜色外其余都相同,现从箱子里随机摸出2个球,恰好为1个黑球和1个红球的概率是________.
13.如图,四边形ABCD为⊙O的内接四边形,已知∠C=∠D,则AB与CD的位置关系是________.
14.如图,△ABC内接于⊙O,AB是⊙O的直径,直线AE是⊙O的切线,CD平分∠ACB,若∠CAE=21°,则∠BFC的度数为________.
三、(每题8分,共16分)
15.我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段AB的最小覆盖圆就是以线段AB为直径的圆.
(1)如图,请分别作出两个三角形的最小覆盖圆;(要求:尺规作图,保留作图痕迹,不写作法)
(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论.(不要求证明)
(第15题)
16.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-1,1),B(-3,1),C(-1,4).
(第16题)
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC绕着点B顺时针旋转90°后得到△A2BC2,请在图中画出△A2BC2,并求出线段BC旋转过程中所扫过的面积(结果保留π).
四、(每题8分,共16分)
17.如图,在一个宁静的夜晚,月光明亮,张芳和身高为1.6 m的李红在人民广场上玩,张芳测得李红的影长AB为1 m,并立刻测得小树的影长CD为1.5 m,请你算一下小树的高度.
(第17题)
18.一个不透明的袋中装有20个只有颜色不同的球,其中有5个黄球,8个黑球,7个红球.
(1)求从袋中摸出1个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀袋中的球,使从袋中摸出1个球是黑球的概率是.求从袋中取出黑球的个数.
五、(每题10分,共20分)
19.一个几何体的三视图如图所示,它的俯视图为菱形,请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.
(第19题)
20.在不透明的袋中有大小、形状和质地等完全相同的小球,它们分别标有数字-1、-2、1、2,从袋中任意摸出一个小球(不放回),将袋中剩余的小球搅匀后,再从袋中摸出另一个小球.
(1)请你表示摸出小球上的数字可能出现的所有结果;
(2)规定:如果摸出的两个小球上的数字都是方程x2-3x+2=0的根,则小明赢.如果摸出的两个小球上的数字都不是方程x2-3x+2=0的根,则小亮赢.你认为这个游戏规则对小明、小亮双方公平吗?请说明理由.
六、(12分)
21.如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4.
(第21题)
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
七、(12分)
22.如图,图①是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图②.已知铁环的半径为5个单位(每个单位为5 cm),设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=.
(1)求点M离地面AC的高度BM(单位:cm);
(2)设人站立点C与点A的水平距离AC等于11个单位,求铁环钩MF的长度(单位:cm).
(第22题)
八、(14分)
23.如图,△ABC为⊙O的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD交AD于E,交AB于F,交⊙O于G.
(1)请判断直线PA与⊙O的位置关系,并说明理由;
(2)求证:AG2=AF·AB;
(3)若⊙O的直径为10,AC=2,AB=4,求△AFG的面积.
(第23题)
答案
一、1.A
2.A 点拨:任意实数的绝对值都大于或等于0.
3.A 4.B 5.D 6.C
7.B 点拨:由三视图知该几何体是圆柱,其底面直径是4,高是6,故这个几何体的侧面积是π×4×6=24π.
8.C 9.D
10.A 点拨:如图,连接OA,OB.∵OA=OB,OM⊥AB,∴∠BOM=∠AOM=∠AOB.∵∠C=∠AOB,
∴∠BOM=∠C.∵BD⊥AC,OM⊥AB,
∴∠CBD+∠C=90°,∠OBM+∠BOM=90°,∴∠CBD=∠OBM.
∵sin∠OBM==OM,
∴sin∠CBD=OM,即sin∠CBD的值等于OM的长.
(第10题)
二、11.80° 12.
13.AB∥CD 14.114°
三、15.解:(1)如图所示.
(第15题)
(2)若三角形为锐角三角形,则其最小覆盖圆为三角形的外接圆;若三角形为直角三角形或钝角三角形,则其最小覆盖圆是以三角形最长边(直角或钝角所对的边)为直径的圆.
16.解:(1)△A1B1C1如图所示.
(2)△A2BC2如图所示.
线段BC旋转过程中所扫过的面积S==.
(第16题)
四、17.解:由题意得=,
即=,
∴CF=1.6×1.5=2.4(m),
即小树的高度为2.4 m.
18.解:(1)20个球里面有5个黄球,故P(摸出1个球是黄球)==.
(2)设从袋中取出x(0
所以=,解得x=2.
经检验,x=2是所列方程的解,且符合实际.所以从袋中取出了2个黑球.
五、19.解:该几何体的形状是直四棱柱.
由三视图知,棱柱底面菱形的对角线长分别为4 cm,3 cm.
∴菱形的边长为 cm,
∴棱柱的侧面积S=×8×4=80(cm2).
20.解:(1)可能出现的所有结果如下表:
-1
-2
1
2
-1
——
(-1,-2)
(-1,1)
(-1,2)
-2
(-2,-1)
——
(-2,1)
(-2,2)
1
(1,-1)
(1,-2)
——
(1,2)
2
(2,-1)
(2,-2)
(2,1)
——
(2)∵x2-3x+2=0,
∴(x-1)(x-2)=0,
∴x1=1,x2=2.
∵共有12种等可能的结果,其中摸出的两个小球上的数字都是方程x2-3x+2=0的根的结果一共有2种,摸出的两个小球上的数字都不是方程的根的结果一共有2种,
∴P(小明赢)=,P(小亮赢)=,
∴游戏规则公平.
六、21.(1)证明:∵AB=AC,
∴∠ABE=∠C.
∵=,∴∠C=∠D.
∴∠ABE=∠D.
又∵∠BAE=∠DAB,
∴△ABE∽△ADB.
(2)解:∵△ABE∽△ADB,
∴=.
∴AB2=AD·AE=(AE+ED)·AE=(2+4)×2=12.∴AB=2.
(3)解:直线FA与⊙O相切.理由如下:
连接OA.∵BD为⊙O的直径,
∴∠BAD=90°.
∴BD===4.
∴BF=BO=BD=2.
又∵AB=2,∴BF=BO=AB.
∴∠F=∠BAF,∠BOA=∠BAO.
∴∠OAF=90°.
又OA为半径,∴直线FA与⊙O相切.
七、22.解:过M作与AC平行的直线,与OA、FC分别相交于H、N,如图.
(1)在Rt△OHM中,∠OHM=90°,OM=5,
所以HM=OM·sinα=3,
所以OH=4,
所以MB=HA=5-4=1,
1×5=5(cm),
所以点M离地面AC的高度BM为5 cm.
(2)易知HN⊥FC,HM⊥OA,∠OMF=90°,所以∠MOH+∠OMH=∠OMH+∠FMN=90°,
所以∠FMN=∠MOH=α,
所以sinα==.
即得FN=FM,
又由(1)知AB=HM=3.
在Rt△FMN中,∠FNM=90°,
易知MN=BC=AC-AB=11-3=8.
由勾股定理得FM2=FN2+MN2,
即FM2=+82,
解得FM=10,
10×5=50(cm),
所以铁环钩MF的长度为50 cm.
(第22题)
八、23.(1)解:PA与⊙O相切.
理由如下:连接CD.
∵AD为⊙O的直径,∴∠ACD=90°.
∴∠D+∠CAD=90°.
∵∠B=∠D,∠PAC=∠B,∴∠PAC=∠D.
∴∠PAC+∠CAD=90°,即DA⊥PA.
∵AD是⊙O的直径,∴PA与⊙O相切.
(2)证明:连接BG.
∵AD为⊙O的直径,CG⊥AD,∴=.
∴∠AGF=∠ABG.
∵∠GAF=∠BAG,∴△AGF∽△ABG.
∴AG∶AB=AF∶AG. ∴AG2=AF·AB.
(3)解:连接BD.
∵AD是⊙O的直径,∴∠ABD=90°.
∵AG2=AF·AB,AG=AC=2,AB=4,∴AF==.
∵CG⊥AD,∴∠AEF=∠ABD=90°.
又∵∠EAF=∠BAD,∴△AEF∽△ABD.
∴=,即=,解得AE=2.
∴EF==1.
∵EG==4,
∴FG=EG-EF=4-1=3.
∴S△AFG=FG·AE=×3×2=3.
同课章节目录
