24.1旋转 第2课时 导学案
图片预览

文档简介
24.1旋转 第二课时 导学案
课题
旋转
单元
24
学科
数学
年级
九年级
知识目标
1.理解中心对称的定义,掌握中心对称的性质..
2.掌握中心对称图形的定义.
重点难点
重点:理解中心对称的定义和中心对称图形的概念,掌握中心对称的性质,并利用中心对称的性质作图
难点:掌握中心对称的性质,并利用中心对称的性质作图.
教学过程
知识链接
1、什么是平移?
2、平移的性质是什么?
合作探究
一、教材第4页
如图,将△ABC绕定点O旋转180°,得到△A’B’C’,这时,图形△ABC与图形△A’B’C’关于点O的对称叫做 ,点O就是 .
归纳中心对称的性质:
,
.
二、教材第4页
例1 如图,已知四边形ABCD和点O,试画出四边形ABCD关于点O成中心对称的图形A'B'C'D'.
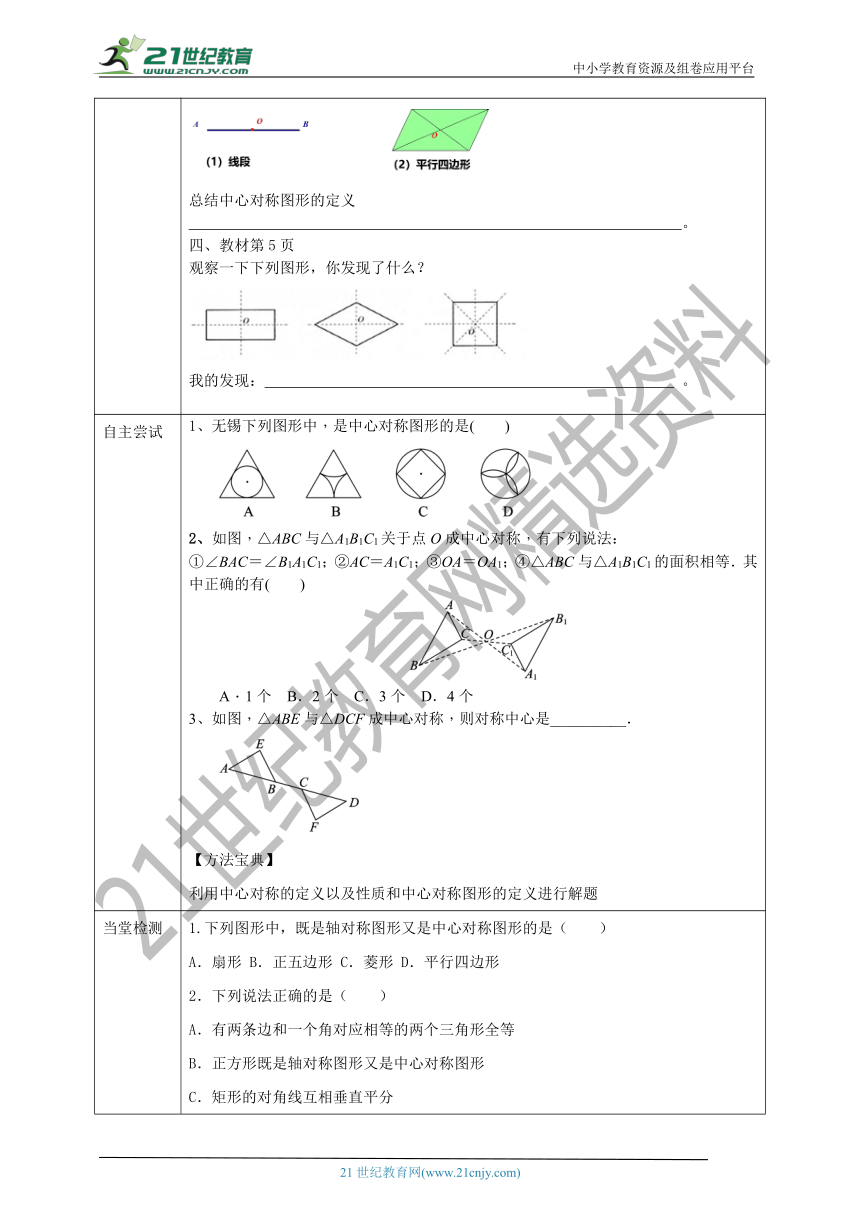
三、教材第5页
将下面的图形绕O点旋转,你有什么发现?
总结中心对称图形的定义
。
四、教材第5页
观察一下下列图形,你发现了什么?
我的发现: 。
自主尝试
1、无锡下列图形中,是中心对称图形的是( )
2、如图,△ABC与△A1B1C1关于点O成中心对称,有下列说法:
①∠BAC=∠B1A1C1;②AC=A1C1;③OA=OA1;④△ABC与△A1B1C1的面积相等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3、如图,△ABE与△DCF成中心对称,则对称中心是__________.
【方法宝典】
利用中心对称的定义以及性质和中心对称图形的定义进行解题
当堂检测
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A.扇形 B.正五边形 C.菱形 D.平行四边形
2.下列说法正确的是( )
A.有两条边和一个角对应相等的两个三角形全等
B.正方形既是轴对称图形又是中心对称图形
C.矩形的对角线互相垂直平分
D.六边形的内角和是540°
3.剪纸是我国传统的民间艺术,下列剪纸作品中既不是轴对称图形,也不是中心对称图形的是( )
A. B.
C. D.
4.下列图形中是中心对称图形的是( )
A. B. C. D.
5.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
6.如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为________.
7.如图,AC=BD,∠A=∠B,点E,F在AB上,且DE∥CF,试说明此图形是中心对称图形.
小结反思
通过本节课的学习,你们有什么收获?
旋转的定义以及性质
参考答案:
当堂检测:
1.C.
2.B.
3.C.
4.C.
5.A
6. 4
7.解:如图,连接CD,交AB于O.
∵在△ACO和△BDO中,∠COA=∠DOB,∠A=∠B,
AC=BD,∴△ACO≌△BDO(AAS),
故OA=OB,OC=OD.
∵DE∥CF,∴∠DEO=∠CFO.
在△ODE和△OCF中,∠DEO=∠CFO,∠DOE=∠COF,OD=OC,
∴△ODE≌△OCF(AAS),
∴OE=OF,∴此图形是中心对称图形.
课题
旋转
单元
24
学科
数学
年级
九年级
知识目标
1.理解中心对称的定义,掌握中心对称的性质..
2.掌握中心对称图形的定义.
重点难点
重点:理解中心对称的定义和中心对称图形的概念,掌握中心对称的性质,并利用中心对称的性质作图
难点:掌握中心对称的性质,并利用中心对称的性质作图.
教学过程
知识链接
1、什么是平移?
2、平移的性质是什么?
合作探究
一、教材第4页
如图,将△ABC绕定点O旋转180°,得到△A’B’C’,这时,图形△ABC与图形△A’B’C’关于点O的对称叫做 ,点O就是 .
归纳中心对称的性质:
,
.
二、教材第4页
例1 如图,已知四边形ABCD和点O,试画出四边形ABCD关于点O成中心对称的图形A'B'C'D'.
三、教材第5页
将下面的图形绕O点旋转,你有什么发现?
总结中心对称图形的定义
。
四、教材第5页
观察一下下列图形,你发现了什么?
我的发现: 。
自主尝试
1、无锡下列图形中,是中心对称图形的是( )
2、如图,△ABC与△A1B1C1关于点O成中心对称,有下列说法:
①∠BAC=∠B1A1C1;②AC=A1C1;③OA=OA1;④△ABC与△A1B1C1的面积相等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3、如图,△ABE与△DCF成中心对称,则对称中心是__________.
【方法宝典】
利用中心对称的定义以及性质和中心对称图形的定义进行解题
当堂检测
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A.扇形 B.正五边形 C.菱形 D.平行四边形
2.下列说法正确的是( )
A.有两条边和一个角对应相等的两个三角形全等
B.正方形既是轴对称图形又是中心对称图形
C.矩形的对角线互相垂直平分
D.六边形的内角和是540°
3.剪纸是我国传统的民间艺术,下列剪纸作品中既不是轴对称图形,也不是中心对称图形的是( )
A. B.
C. D.
4.下列图形中是中心对称图形的是( )
A. B. C. D.
5.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
6.如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为________.
7.如图,AC=BD,∠A=∠B,点E,F在AB上,且DE∥CF,试说明此图形是中心对称图形.
小结反思
通过本节课的学习,你们有什么收获?
旋转的定义以及性质
参考答案:
当堂检测:
1.C.
2.B.
3.C.
4.C.
5.A
6. 4
7.解:如图,连接CD,交AB于O.
∵在△ACO和△BDO中,∠COA=∠DOB,∠A=∠B,
AC=BD,∴△ACO≌△BDO(AAS),
故OA=OB,OC=OD.
∵DE∥CF,∴∠DEO=∠CFO.
在△ODE和△OCF中,∠DEO=∠CFO,∠DOE=∠COF,OD=OC,
∴△ODE≌△OCF(AAS),
∴OE=OF,∴此图形是中心对称图形.
