人教A版高中数学必修一 课件:2.2.1 第二课时 对数的运算 :36张PPT
文档属性
| 名称 | 人教A版高中数学必修一 课件:2.2.1 第二课时 对数的运算 :36张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 22:38:19 | ||
图片预览











文档简介
课件36张PPT。第二课时 对数的运算[目标导航]新知导学·素养养成1.对数的运算性质
如果a>0,且a≠1,M>0,N>0,那么:
(1)loga(M·N)= ;logaM+logaNlogaM-logaN(3)logaMn= (n∈R).nlogaM思考1:loga(MN)=logaM+logaN是否成立?
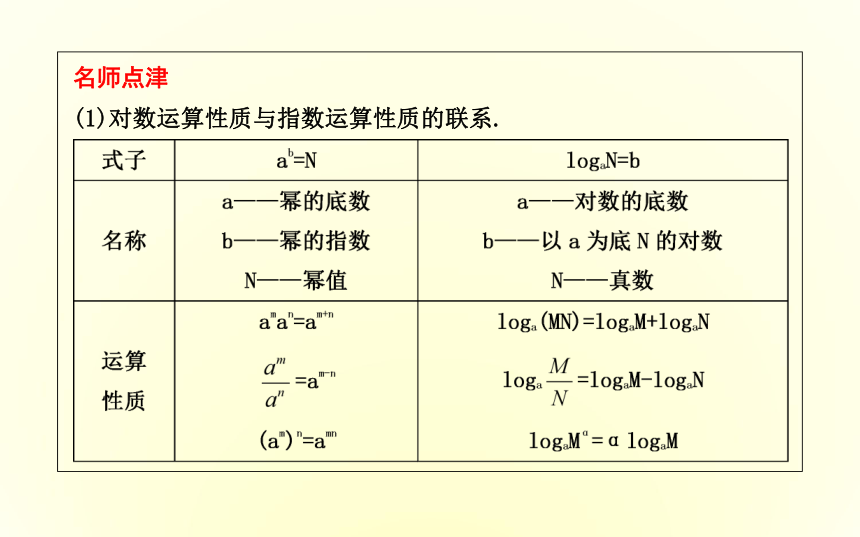
答案:不一定,当M>0且N>0时,该式成立,当M<0,N<0时,该式不成立.思考2:你能用对数定义证明对数换底公式吗?名师点津(1)对数运算性质与指数运算性质的联系.③logab·logba=1;
④logab·logbc·logcd=logad.课堂探究·素养提升解:(2)原式=2lg 5+2lg 2+(lg 10-lg 2)(lg 10+lg 2)+(lg 2)2= 2lg 10+1-(lg 2)2+(lg 2)2=2+1=3.方法技巧(1)本题主要考查对数式的化简与计算.解决这类问题一般有两种思路:一是将式中真数的积、商、幂、方根运用对数的运算性质将它们化为对数的和、差、积、商,然后化简求值;二是将式中对数的和、差、积、商逆用对数的运算性质化为真数的积、商、幂、方根,然后化简求值.
(2)对数计算问题中,涉及lg 2,lg 5时,常利用lg 2+lg 5=1及lg 2=1-lg 5,lg 5=1-lg 2等解题.答案:(1)B答案:(2)-4解:(1)①loga(x3y2z)=logax3+logay2+logaz=3logax+2logay+logaz.解:(2)①原式=2log32-(log332-log39)+3log32
=2log32-5log32+log39+3log32=2.方法技巧(1)在化简或计算求值时,若已知式子中含不同底数,则常利用对数换底公式转化为同底数对数后求解.(2)已知2a=3,3b=7,则log756= .(结果用a,b表示)?(3)已知log89=a,log25=b,用a,b表示lg 3.(2)26a=33b=62c,求a,b,c之间的关系.方法技巧(1)涉及指数式中的指数问题,可利用指对数式的互化,将指数式化为对数式后求指数.
(2)涉及多个幂式相等问题,常将幂式值设出,转化为对数后求解.(2)已知logax=2,logbx=3,logcx=6,求logabcx.题型四 易错辨析
[例4] 解方程lg x4-lg x2=2.错解:因为lg x4-lg x2=2,
所以4lg x-2lg x=2,
所以lg x=1,所以x=10.纠错:已知方程中x的取值范围是x∈R且x≠0,而变形后的x范围是x>0,缩小了x的范围,从而失根.学霸经验分享区(1)对数的化简求值一般是正用或逆用公式,对真数进行处理,选哪种策略化简,取决于问题的实际情况,一般本着便于真数化简的原则进行.
(2)利用对数的换底公式能够将不同底的对数化为常用对数或自然对数或同底的对数,即可用对数的运算性质来解决对数求值问题,同时要注意换底公式的逆用和变形用.
(3)求解对数方程时,要注意等价变形,不要扩大或缩小x的范围.如解方程log5(2x+1)=log5(x2-2),则变形为2x+1=x2-2后要保证2x+1> 0,x2-2>0,因此由x2-2=2x+1得x=3或x=-1后应舍去x=-1.课堂达标解析:由对数的运算性质易知C正确.1.下列等式成立的是( )CA3.下列式子中正确的个数是( )
①若lg a=lg b,则lg a2=lg b2;
②若lg a2=lg b2,则a=b;
③若lg a3=lg b3,则a=b;
④logax+2logay=loga(xy2)(a,x,y使式子有意义).
(A)1 (B)2 (C)3 (D)4C解析:当lg a=lg b时,一定有lg a2=lg b2,反之不一定成立.
当lg a3=lg b3时,可得3lg a=3lg b,
即lg a=lg b,则a=b.
logax+2logay=loga(xy2).
故①③④正确.故选C.5.(2018·北京市西城13中高一上学期期中)已知ln 2=a,ln 3=b,那么log32用含a,b的代数式表示为 .?
如果a>0,且a≠1,M>0,N>0,那么:
(1)loga(M·N)= ;logaM+logaNlogaM-logaN(3)logaMn= (n∈R).nlogaM思考1:loga(MN)=logaM+logaN是否成立?
答案:不一定,当M>0且N>0时,该式成立,当M<0,N<0时,该式不成立.思考2:你能用对数定义证明对数换底公式吗?名师点津(1)对数运算性质与指数运算性质的联系.③logab·logba=1;
④logab·logbc·logcd=logad.课堂探究·素养提升解:(2)原式=2lg 5+2lg 2+(lg 10-lg 2)(lg 10+lg 2)+(lg 2)2= 2lg 10+1-(lg 2)2+(lg 2)2=2+1=3.方法技巧(1)本题主要考查对数式的化简与计算.解决这类问题一般有两种思路:一是将式中真数的积、商、幂、方根运用对数的运算性质将它们化为对数的和、差、积、商,然后化简求值;二是将式中对数的和、差、积、商逆用对数的运算性质化为真数的积、商、幂、方根,然后化简求值.
(2)对数计算问题中,涉及lg 2,lg 5时,常利用lg 2+lg 5=1及lg 2=1-lg 5,lg 5=1-lg 2等解题.答案:(1)B答案:(2)-4解:(1)①loga(x3y2z)=logax3+logay2+logaz=3logax+2logay+logaz.解:(2)①原式=2log32-(log332-log39)+3log32
=2log32-5log32+log39+3log32=2.方法技巧(1)在化简或计算求值时,若已知式子中含不同底数,则常利用对数换底公式转化为同底数对数后求解.(2)已知2a=3,3b=7,则log756= .(结果用a,b表示)?(3)已知log89=a,log25=b,用a,b表示lg 3.(2)26a=33b=62c,求a,b,c之间的关系.方法技巧(1)涉及指数式中的指数问题,可利用指对数式的互化,将指数式化为对数式后求指数.
(2)涉及多个幂式相等问题,常将幂式值设出,转化为对数后求解.(2)已知logax=2,logbx=3,logcx=6,求logabcx.题型四 易错辨析
[例4] 解方程lg x4-lg x2=2.错解:因为lg x4-lg x2=2,
所以4lg x-2lg x=2,
所以lg x=1,所以x=10.纠错:已知方程中x的取值范围是x∈R且x≠0,而变形后的x范围是x>0,缩小了x的范围,从而失根.学霸经验分享区(1)对数的化简求值一般是正用或逆用公式,对真数进行处理,选哪种策略化简,取决于问题的实际情况,一般本着便于真数化简的原则进行.
(2)利用对数的换底公式能够将不同底的对数化为常用对数或自然对数或同底的对数,即可用对数的运算性质来解决对数求值问题,同时要注意换底公式的逆用和变形用.
(3)求解对数方程时,要注意等价变形,不要扩大或缩小x的范围.如解方程log5(2x+1)=log5(x2-2),则变形为2x+1=x2-2后要保证2x+1> 0,x2-2>0,因此由x2-2=2x+1得x=3或x=-1后应舍去x=-1.课堂达标解析:由对数的运算性质易知C正确.1.下列等式成立的是( )CA3.下列式子中正确的个数是( )
①若lg a=lg b,则lg a2=lg b2;
②若lg a2=lg b2,则a=b;
③若lg a3=lg b3,则a=b;
④logax+2logay=loga(xy2)(a,x,y使式子有意义).
(A)1 (B)2 (C)3 (D)4C解析:当lg a=lg b时,一定有lg a2=lg b2,反之不一定成立.
当lg a3=lg b3时,可得3lg a=3lg b,
即lg a=lg b,则a=b.
logax+2logay=loga(xy2).
故①③④正确.故选C.5.(2018·北京市西城13中高一上学期期中)已知ln 2=a,ln 3=b,那么log32用含a,b的代数式表示为 .?
