人教版七年级数学下册第九章 不等式与不等式组9.1.2不等式的性质 课件 (2课时共56张)
文档属性
| 名称 | 人教版七年级数学下册第九章 不等式与不等式组9.1.2不等式的性质 课件 (2课时共56张) |  | |
| 格式 | zip | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 16:40:53 | ||
图片预览










文档简介
课件56张PPT。9.1 不等式第一课时第二课时人教版 数学 七年级 下册9.1.2 不等式的性质不等式的三个性质第一课时返回等式的基本性质:
(1)等式的两边都加上(或都减去)同一个
数或同一个整式,等式仍然成立.
(2)等式的两边都乘以(或除以)一个不为0
的数,等式仍然成立.
猜想 :不等式也具有同样的性质吗?2. 能够利用不等式的性质解不等式.1. 掌握不等式的三个性质.素养目标3. 通过实例操作,培养学生观察、分析、比较问题的能力.等式基本性质1:
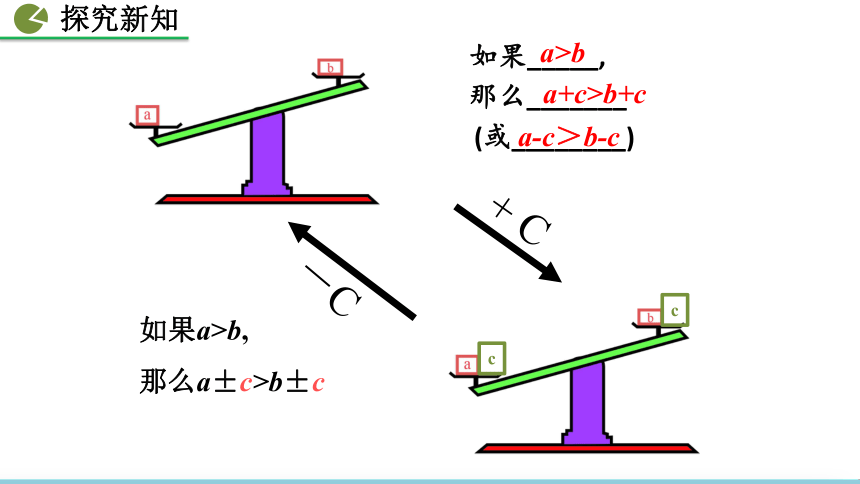
等式的两边都加上(或减去)同一个整式,等式仍然成立.如果a=b,那么a±c=b±c不等式的性质1不等式是否具有类似的性质呢?如果 7 > 3,那么 7+5 ____ 3+ 5 , 7 -5____3-5你能总结一下规律吗?>>如果-1< 3,
那么-1+2____3+2, -1- 4____3 - 4<<+ C-C(或________)如果_____,那么_______如果a>b,
那么a±c>b±ca>ba+c>b+ca-c>b-c 不等式的两边都加上(或减去)同一个整式,不等号的方向不变.如果____,那么_________.a>ba±c>b±c不等式基本性质1: 解:因为 a>b,两边都加上3, 解:因为 a b+3; 由不等式基本性质1,得 a-5 < b-5 .(1)已知 a>b,则a+3 b+3(2)已知 a < 例1 用“>”或“<”填空:利用不等式的性质1解答问题1.用“>”或“<”填空,并说明是根据不等式的哪一条性质:
(1)若x+3>6,则x______3,
根据______________;
(2)若a-2<3,则a______5,
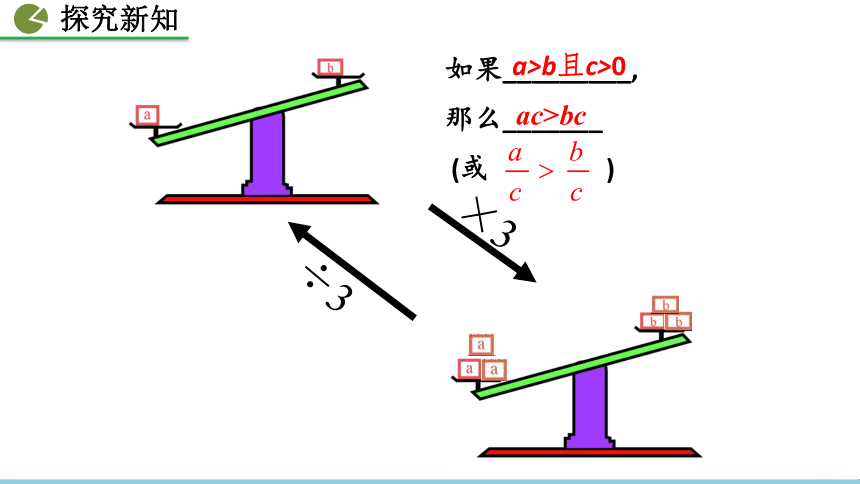
根据____________.> < 不等式性质1不等式性质1 用不等号填空:(1)5 3 ; 5×2 3×2 ;5÷2 3÷2 .> > > < < < 自己再写一个不等式,分别在它的两边都乘(或除以)同一个正数,看看有怎样的结果?与同桌互相交流,你们发现了什么规律?不等式的性质2×3÷3(或 )如果_________,那么_______a>b且c>0ac>bc 如果a > b,c > 0,那么 ac > bc , > . 不等式的两边都乘(或除以)同一个正数,
不等号的方向不变.不等式基本性质2例2 设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质. (1) a÷3____b÷3
(2) 0.1a____0.1b;
(3) 2a+3____2b+3;
(4)(m2+1)a____ (m2+1)b(m为常数)>>>>不等式的性质2不等式的性质2不等式的性质1,2不等式的性质2利用不等式的性质2解答问题-8<47×5___ 4×5-8÷2___ 4÷2不变不变7>4.........><2.完成下表: 用不等号填空:(1)5 3 ; 5×(-2) 3×(-2) ;5÷(-2) 3÷(-2) .> < < < > > 自己再写一个不等式,分别在它的两边都乘(或除以)同一个负数,看看有怎样的结果?与同桌互相交流,你们发现了什么规律?不等式的性质3a>ba-a-b>b-a-b不等式两边同乘以-1,不等号方向改变.猜想:不等式两边同乘以一个负数,不等号方向改变.-ac<-bc 如果a > b,c < 0,那么 ac < bc , < .不等式基本性质3 不等式的两边都乘(或除以)同一个负数,不等号的方向改变. (1)如果a>b,那么ac>bc.
(2)如果a>b,那么ac2>bc2.
(3)如果ac2>bc2,那么a>b.你能用不等式的基本性质判断下列说法的正误吗?××√ 因为c≠0,所以c2>0.当c≤0时,不成立.当c=0时,不成立.不等式的基本性质与等式的基本性质有什么相同点和不同点? 因为 a>b,两边都乘3,因为 a>b,两边都乘-1,解:由不等式基本性质2,得 3a > 3b.由不等式基本性质3,得-a < -b. (1)已知 a>b,则3a 3b ;(2)已知 a>b,则-a -b .><例3 用“>”或“<”填空:利用不等式的性质解答问题解: 因为 a 因为 ,两边都加上2,解:3.若 a>b, 用“>”或“<”填空:
a-5 b-5(根据不等式的性质 )
6a 6b(根据不等式的性质 )
2a+4 2b+4 (根据不等式的性质 )
(根据不等式的性质 )>1<3和1>>22和1 等式有对称性及传递性,那么不等式具有对称性和传递性吗?已知x>5,那么55 5b,那么bb,b>c,那么a>c.例4 利用不等式的性质解下列不等式:
(1)x-7>26; (2)3x<2x+1;
(3) ; (4)-4x>3. 利用不等式的性质解不等式分析:解未知数为x的不等式,就是要使不等式逐步化为x>a或x<a的形式.解:(1)为了使不等式x-7>26中不等号的一边变为x,根据不等式的性质1,不等式两边都加7,不等号的方向不变,得 x-7+7 > 26+7,
x > 33.这个不等式的解集在数轴上的表示如图所示: (2)为了使不等式3x<2x+1中不等号的一边变为x,根据_____________,不等式两边都减去____,不等号的方向_____,得3x-2x<2x+1-2x, x<1.这个不等式的解集在数轴上的表示如图所示:不等式性质12x不变(3)为了使不等式 中不等号的一边变为x,根据不等式的性质2,不等式的两边都除以 不等号的方向不变,
得x>75这个不等式的解集在数轴上的表示如图所示:(4)为了使不等式-4x>3中的不等号的一边变为x,根据
______________,不等式两边都除以____,不等号的方
向______,得这个不等式的解集在数轴上的表示如图所示:不等式的性质3-4改变4.利用不等式的性质解下列不等式.(2)-2x > 3(1)x-5 > -1(3)7x < 6x-6解:x>-1+57x-6x<-6例5 如果不等式 (a+1)x<a+1可变形为 x>1,那么a 必须满足________.解析:根据不等式的基本性质可判断,a+1为负数,即a+1<0,可得 a<-1. a<-1利用不等式的性质确定字母的值提示:只有当不等式的两边都乘(或除以)一个负数时,
不等号的方向才改变.5.a是任意有理数,试比较5a与3a的大小.这种解法对吗?如果正确,说出它根据的是不等式的哪一条基本性质;如果不正确,请就明理由.答:这种解法不正确,因为字母a的取值范围我们并不知道.如果 a<0,那么 5a < 3a ;如果a=0 ,那么 5a = 3a . 1.(2019?桂林)如果a>b,c<0,那么下列不等式成立的是
( )
A.a+c>b B.a+c>b﹣c
C.ac﹣1>bc﹣1 D.a(c﹣1)<b(c﹣1) 巩固练习2.(2019?大连)不等式5x+1≥3x﹣1的解集在数轴上表示正确的是( )
A. B.
C. D. DB1.若x>y,则ax >ay,那么一定有( )
A.a>0 B. a ≥0 C. a<0 D. a ≤0
2.与x-2< 0 的解集相同的是 ( )
A. x>1 B. x< 2 C. x<1 D. x ≤ 2
AB 3. 已知a < b,用“>”或“<”填空: (1)a +12 b +12 ; (2)b-10 a -10 .<>解:x < 2解:x < 64. 把下列不等式化为x>a或x 3(1)x-5 > -1(3)7x < 6x-6x>4 x<-6由不等式3<6 ,李毅和浩轩分别得出的以下两个不等式对吗?
(1)李毅:3-a<6-a
(2)浩轩:3a<6a解:(1)3<6,根据不等式的性质1得,3-a<6-a (2)3<6,当a>0时,根据不等式的性质2得,3a<6a 当a<0时,根据不等式的性质3得,3a>6a.已知不等式2a+3b>3a+ 2b,试比较a、b的大小.解:根据不等式的基本性质1,不等式两边都减去(2a+2b),得
2a+3b- (2a+2b)>3a+ 2b - (2a+2b)
2a+3b-2a - 2b>3a+ 2b - 2a - 2b
b>a不等式的基本性质不等式基本性质2不等式基本性质3→→如果
那么如果 那么
应用不等式基本性质1如果a>b,那么a+c>b+c,
a-c>b-c→含“≤”“≥”的不等式第二课时返回问题 前面学过哪几种形式的不等式? 学过用符号“<”“>”或“≠ ”连接的式子叫做不等式.【想一想】 写出下列图片信息中的含义:八达岭长城
11月06天气:
小雪?-2~0℃1. 进一步了解不等式的概念,认识几种不等号的含义. 2. 学会并准确运用不等式表示数量关系,形成在表达中渗透数形结合的思想.素养目标 一辆轿车在一条规定车速不低于60km/h,且不高于100 km/h的高速公路上行驶,如何用式子来表示轿车在该高速公路上行驶的路程s(km)与行驶时间x(h)之间的关系呢?根据路程与速度、时间之间的关系可得:s≥60x,且s≤100x. 铁路部门对随身携带的行李有如下规定:每件行李的长、宽、高之和不得超过160cm.设行李的长、宽、高分别为acm,bcm,ccm,请你列出行李的长、宽、高满足的关系式. 根据题意可得: a+b+c≤160.常用的表示不等关系的关键词语及对应的不等号<>≥≤>0<0≥0≤0 我们把用不等号(>,<,≥,≤,≠)连接而成的式子叫作不等式.其中“≥”读作大于等于,“≤”读作小于等于.例1 某长方体形状的容器长5cm,宽3cm,高10cm,容器内原有水的高度为3cm,现准备向它继续注水.用V(单位:cm3)表示新注入水的体积,写出V的取值范围.利用不等式解答实际问题解:新注入水的体积V与原有水的体积的和不能超过容器的容积,即V+3×5×3≤3×5×10解得 V≤105又由于新注入水的体积不能是负数,因此,V的取值范围是V≥0并且V≤105.在数轴上表示V的取值范围如图在表示0和105的点上画实心圆点,表示取值范围包括这两个数
归纳总结利用不等式的性质解不等式的注意事项2.要注意区分“大于” “不大于”“小于”“不小于”
等数学语言的使用,并把这些表示不等关系的语言用数
学符号准确地表达出来.3.在数轴上表示解集应注意的问题:方向、空心或实心.1.在运用性质3时,要特别注意:不等式两边都乘以或除以同一个负数时,要改变不等号的方向.1.某种商品的进价为800元,出售标价为1 200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则最多可打( )
A.6折 B.7折 C.8折 D.9折 解析:设打x折,由题意得1 200×10x%-800≥800×5%,
解得x≥7,即最多可打7折 .故选B.B(2019?贵阳模拟)关于x的不等式的解集在数轴上表示如图所示,则该不等式的解集为___________. 巩固练习x≤2 1.如图所示,把不等式x≥-1的解集在数轴上表示出来,正确的是 ( )
A. B.
C. D.B 2.下列数值中不是不等式5x≥2x+9的解的是( )
A.5 B.4 C.3 D.2D 3.用不等式表示下列语句并写出解集,并在数轴
上表示解集.(1)x的3倍大于或等于1;(2)x与3的和不小于6;(3)y与1的差不大于0;分析:本题中属于第一类表示数量不等关系的关键词语.即大于或等于、不小于都用“ ≥”表示;不大于、小于或等于都用“≤”表示. (4)y的 小于或等于-2.解:(1)3x≥1, 解集是 ;(2)x+3≥6, 解集是x≥3;(3)y-1≤0, 解集是y≤1;(4) , 解集是y≤-8. 用炸药爆破时,如果导火索燃烧的速度是0.8 cm/s,人跑开的速度是每秒4 m,为了使点导火索的战士在爆破时能够跑到100 m以外的安全区域,这个导火索的长度应大于多少厘米?解:设导火索的长度是x cm .根据题意,得
×4>100.
答:导火索的长度应大于20 cm.
解得: x>20 小希就读的学校上午第一节课上课时间是8点开始.小希家距学校有2千米,而她的步行速度为每小时10千米.那么,小希上午几点从家里出发才能保证不迟到?解:设小希上午x点从家里出发才能不迟到,根据题意得: 答:小希上午7:48前时从家里出发才能不迟到.解得 路上的时间2÷10=一个概念:不等式两种思想:数学建模、类比等式三个注意:一要注意“负数”、“非负数”、“不大于”、“不小于”等关键词语的含义;
二要注意仔细审题,正确列出不等式;
三要注意观察生活,让数学服务生活。课后作业作业
内容教材作业从课后习题中选取自主安排配套练习册练习
(1)等式的两边都加上(或都减去)同一个
数或同一个整式,等式仍然成立.
(2)等式的两边都乘以(或除以)一个不为0
的数,等式仍然成立.
猜想 :不等式也具有同样的性质吗?2. 能够利用不等式的性质解不等式.1. 掌握不等式的三个性质.素养目标3. 通过实例操作,培养学生观察、分析、比较问题的能力.等式基本性质1:
等式的两边都加上(或减去)同一个整式,等式仍然成立.如果a=b,那么a±c=b±c不等式的性质1不等式是否具有类似的性质呢?如果 7 > 3,那么 7+5 ____ 3+ 5 , 7 -5____3-5你能总结一下规律吗?>>如果-1< 3,
那么-1+2____3+2, -1- 4____3 - 4<<+ C-C(或________)如果_____,那么_______如果a>b,
那么a±c>b±ca>ba+c>b+ca-c>b-c 不等式的两边都加上(或减去)同一个整式,不等号的方向不变.如果____,那么_________.a>ba±c>b±c不等式基本性质1: 解:因为 a>b,两边都加上3, 解:因为 a
(1)若x+3>6,则x______3,
根据______________;
(2)若a-2<3,则a______5,
根据____________.> < 不等式性质1不等式性质1 用不等号填空:(1)5 3 ; 5×2 3×2 ;5÷2 3÷2 .> > > < < < 自己再写一个不等式,分别在它的两边都乘(或除以)同一个正数,看看有怎样的结果?与同桌互相交流,你们发现了什么规律?不等式的性质2×3÷3(或 )如果_________,那么_______a>b且c>0ac>bc 如果a > b,c > 0,那么 ac > bc , > . 不等式的两边都乘(或除以)同一个正数,
不等号的方向不变.不等式基本性质2例2 设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质. (1) a÷3____b÷3
(2) 0.1a____0.1b;
(3) 2a+3____2b+3;
(4)(m2+1)a____ (m2+1)b(m为常数)>>>>不等式的性质2不等式的性质2不等式的性质1,2不等式的性质2利用不等式的性质2解答问题-8<47×5___ 4×5-8÷2___ 4÷2不变不变7>4.........><2.完成下表: 用不等号填空:(1)5 3 ; 5×(-2) 3×(-2) ;5÷(-2) 3÷(-2) .> < < < > > 自己再写一个不等式,分别在它的两边都乘(或除以)同一个负数,看看有怎样的结果?与同桌互相交流,你们发现了什么规律?不等式的性质3a>ba-a-b>b-a-b不等式两边同乘以-1,不等号方向改变.猜想:不等式两边同乘以一个负数,不等号方向改变.-ac<-bc 如果a > b,c < 0,那么 ac < bc , < .不等式基本性质3 不等式的两边都乘(或除以)同一个负数,不等号的方向改变. (1)如果a>b,那么ac>bc.
(2)如果a>b,那么ac2>bc2.
(3)如果ac2>bc2,那么a>b.你能用不等式的基本性质判断下列说法的正误吗?××√ 因为c≠0,所以c2>0.当c≤0时,不成立.当c=0时,不成立.不等式的基本性质与等式的基本性质有什么相同点和不同点? 因为 a>b,两边都乘3,因为 a>b,两边都乘-1,解:由不等式基本性质2,得 3a > 3b.由不等式基本性质3,得-a < -b. (1)已知 a>b,则3a 3b ;(2)已知 a>b,则-a -b .><例3 用“>”或“<”填空:利用不等式的性质解答问题解: 因为 a
a-5 b-5(根据不等式的性质 )
6a 6b(根据不等式的性质 )
2a+4 2b+4 (根据不等式的性质 )
(根据不等式的性质 )>1<3和1>>22和1 等式有对称性及传递性,那么不等式具有对称性和传递性吗?已知x>5,那么5
(1)x-7>26; (2)3x<2x+1;
(3) ; (4)-4x>3. 利用不等式的性质解不等式分析:解未知数为x的不等式,就是要使不等式逐步化为x>a或x<a的形式.解:(1)为了使不等式x-7>26中不等号的一边变为x,根据不等式的性质1,不等式两边都加7,不等号的方向不变,得 x-7+7 > 26+7,
x > 33.这个不等式的解集在数轴上的表示如图所示: (2)为了使不等式3x<2x+1中不等号的一边变为x,根据_____________,不等式两边都减去____,不等号的方向_____,得3x-2x<2x+1-2x, x<1.这个不等式的解集在数轴上的表示如图所示:不等式性质12x不变(3)为了使不等式 中不等号的一边变为x,根据不等式的性质2,不等式的两边都除以 不等号的方向不变,
得x>75这个不等式的解集在数轴上的表示如图所示:(4)为了使不等式-4x>3中的不等号的一边变为x,根据
______________,不等式两边都除以____,不等号的方
向______,得这个不等式的解集在数轴上的表示如图所示:不等式的性质3-4改变4.利用不等式的性质解下列不等式.(2)-2x > 3(1)x-5 > -1(3)7x < 6x-6解:x>-1+57x-6x<-6例5 如果不等式 (a+1)x<a+1可变形为 x>1,那么a 必须满足________.解析:根据不等式的基本性质可判断,a+1为负数,即a+1<0,可得 a<-1. a<-1利用不等式的性质确定字母的值提示:只有当不等式的两边都乘(或除以)一个负数时,
不等号的方向才改变.5.a是任意有理数,试比较5a与3a的大小.这种解法对吗?如果正确,说出它根据的是不等式的哪一条基本性质;如果不正确,请就明理由.答:这种解法不正确,因为字母a的取值范围我们并不知道.如果 a<0,那么 5a < 3a ;如果a=0 ,那么 5a = 3a . 1.(2019?桂林)如果a>b,c<0,那么下列不等式成立的是
( )
A.a+c>b B.a+c>b﹣c
C.ac﹣1>bc﹣1 D.a(c﹣1)<b(c﹣1) 巩固练习2.(2019?大连)不等式5x+1≥3x﹣1的解集在数轴上表示正确的是( )
A. B.
C. D. DB1.若x>y,则ax >ay,那么一定有( )
A.a>0 B. a ≥0 C. a<0 D. a ≤0
2.与x-2< 0 的解集相同的是 ( )
A. x>1 B. x< 2 C. x<1 D. x ≤ 2
AB 3. 已知a < b,用“>”或“<”填空: (1)a +12 b +12 ; (2)b-10 a -10 .<>解:x < 2解:x < 64. 把下列不等式化为x>a或x
(1)李毅:3-a<6-a
(2)浩轩:3a<6a解:(1)3<6,根据不等式的性质1得,3-a<6-a (2)3<6,当a>0时,根据不等式的性质2得,3a<6a 当a<0时,根据不等式的性质3得,3a>6a.已知不等式2a+3b>3a+ 2b,试比较a、b的大小.解:根据不等式的基本性质1,不等式两边都减去(2a+2b),得
2a+3b- (2a+2b)>3a+ 2b - (2a+2b)
2a+3b-2a - 2b>3a+ 2b - 2a - 2b
b>a不等式的基本性质不等式基本性质2不等式基本性质3→→如果
那么如果 那么
应用不等式基本性质1如果a>b,那么a+c>b+c,
a-c>b-c→含“≤”“≥”的不等式第二课时返回问题 前面学过哪几种形式的不等式? 学过用符号“<”“>”或“≠ ”连接的式子叫做不等式.【想一想】 写出下列图片信息中的含义:八达岭长城
11月06天气:
小雪?-2~0℃1. 进一步了解不等式的概念,认识几种不等号的含义. 2. 学会并准确运用不等式表示数量关系,形成在表达中渗透数形结合的思想.素养目标 一辆轿车在一条规定车速不低于60km/h,且不高于100 km/h的高速公路上行驶,如何用式子来表示轿车在该高速公路上行驶的路程s(km)与行驶时间x(h)之间的关系呢?根据路程与速度、时间之间的关系可得:s≥60x,且s≤100x. 铁路部门对随身携带的行李有如下规定:每件行李的长、宽、高之和不得超过160cm.设行李的长、宽、高分别为acm,bcm,ccm,请你列出行李的长、宽、高满足的关系式. 根据题意可得: a+b+c≤160.常用的表示不等关系的关键词语及对应的不等号<>≥≤>0<0≥0≤0 我们把用不等号(>,<,≥,≤,≠)连接而成的式子叫作不等式.其中“≥”读作大于等于,“≤”读作小于等于.例1 某长方体形状的容器长5cm,宽3cm,高10cm,容器内原有水的高度为3cm,现准备向它继续注水.用V(单位:cm3)表示新注入水的体积,写出V的取值范围.利用不等式解答实际问题解:新注入水的体积V与原有水的体积的和不能超过容器的容积,即V+3×5×3≤3×5×10解得 V≤105又由于新注入水的体积不能是负数,因此,V的取值范围是V≥0并且V≤105.在数轴上表示V的取值范围如图在表示0和105的点上画实心圆点,表示取值范围包括这两个数
归纳总结利用不等式的性质解不等式的注意事项2.要注意区分“大于” “不大于”“小于”“不小于”
等数学语言的使用,并把这些表示不等关系的语言用数
学符号准确地表达出来.3.在数轴上表示解集应注意的问题:方向、空心或实心.1.在运用性质3时,要特别注意:不等式两边都乘以或除以同一个负数时,要改变不等号的方向.1.某种商品的进价为800元,出售标价为1 200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则最多可打( )
A.6折 B.7折 C.8折 D.9折 解析:设打x折,由题意得1 200×10x%-800≥800×5%,
解得x≥7,即最多可打7折 .故选B.B(2019?贵阳模拟)关于x的不等式的解集在数轴上表示如图所示,则该不等式的解集为___________. 巩固练习x≤2 1.如图所示,把不等式x≥-1的解集在数轴上表示出来,正确的是 ( )
A. B.
C. D.B 2.下列数值中不是不等式5x≥2x+9的解的是( )
A.5 B.4 C.3 D.2D 3.用不等式表示下列语句并写出解集,并在数轴
上表示解集.(1)x的3倍大于或等于1;(2)x与3的和不小于6;(3)y与1的差不大于0;分析:本题中属于第一类表示数量不等关系的关键词语.即大于或等于、不小于都用“ ≥”表示;不大于、小于或等于都用“≤”表示. (4)y的 小于或等于-2.解:(1)3x≥1, 解集是 ;(2)x+3≥6, 解集是x≥3;(3)y-1≤0, 解集是y≤1;(4) , 解集是y≤-8. 用炸药爆破时,如果导火索燃烧的速度是0.8 cm/s,人跑开的速度是每秒4 m,为了使点导火索的战士在爆破时能够跑到100 m以外的安全区域,这个导火索的长度应大于多少厘米?解:设导火索的长度是x cm .根据题意,得
×4>100.
答:导火索的长度应大于20 cm.
解得: x>20 小希就读的学校上午第一节课上课时间是8点开始.小希家距学校有2千米,而她的步行速度为每小时10千米.那么,小希上午几点从家里出发才能保证不迟到?解:设小希上午x点从家里出发才能不迟到,根据题意得: 答:小希上午7:48前时从家里出发才能不迟到.解得 路上的时间2÷10=一个概念:不等式两种思想:数学建模、类比等式三个注意:一要注意“负数”、“非负数”、“不大于”、“不小于”等关键词语的含义;
二要注意仔细审题,正确列出不等式;
三要注意观察生活,让数学服务生活。课后作业作业
内容教材作业从课后习题中选取自主安排配套练习册练习
